Cochain operators

Redirect to:

• Cohomology#Homology vs. cohomology maps

Given a map $f \colon X \rightarrow Y$, we will investigate what relation $f$ establishes between the cohomology classes in $X$ and those of $Y$.

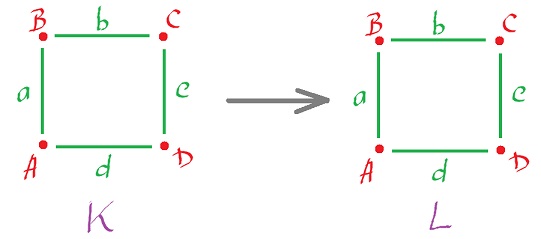
Again, we limit our attention to $X$ and $Y$ which are realizations of cubical complexes, say $K$ and $L$: $$X = |K|, Y = |L|.$$

Then, we need an analogue of maps in this environment, i.e., given a map $f$ we build such a "combinatorial" construction involving complexes $K$ and $L$ that its "realization" is $f$.

Suppose we have a cell map: $$g \colon X \rightarrow Y.$$ We define function $g_k$ on chains as follows:

(A) $g_k$ maps each $k$-cell in $X$ to a $k$-cell in $Y$ (or $0$).

This condition simply means that $g_k$ maps $k$-chains to $k$-chains: $$g_k \colon C_k(K) \rightarrow C_k(L), k = 0, 1, 2, ...,$$

As before, we also require:

(B) $g$ preserves boundaries,

or, algebraically, $$\partial g = g \partial .$$ So, it's a chain map.

These two conditions also ensure that $g_k$ and, therefore, $g$ itself induces a cochain operators or map, a function on cochains. How?

Recall that $C^k$ is the dual of $C_k$: $$C^k=(C_k)^*,$$ and every operator on the former generates an operator on the latter, as follows. Given, as above, a chain map $$g_k:C_k(K) \rightarrow C_k(L),$$ its dual goes in the opposite direction: $$g^k=(g_k)^*:C^k(L) \rightarrow C^k(K).$$

This is how it is defined: $$g^k(\phi)=g_k \circ \phi,$$ for each cochain $\phi \in C^k(L).$ This is how this works: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & C_k(K) & \ra{g_k} & C_k(L) \\ & _{\psi \in C^k(K)} & \searrow & \da{\phi \in C^k(L)} \\ & & & {\bf R} \end{array} $$

Let's consider maps of the circle to itself $$g \colon X = {\bf S}^1 \rightarrow Y = {\bf S}^1.$$

We've already considered a few examples of computation of homology operators. Now cohomology.

For every cell $x$ in $K,L$, let $\phi_x$ denote the cochain that is $1$ on $x$ and $0$ elsewhere.

Identity: $$\begin{array}{l} g_0(A) = A, g_0(B) = B, g_0(C) = C, g_0(D) = D \Rightarrow g^0(\phi_A) = \phi_A, g^0(\phi_B) = \phi_B, g^0(\phi_C) = \phi_C, g^0(\phi_D) = \phi_D,\\ g_1(a) = a, g_1(b) = b, g_1(c) = c, g_1(d) = d \Rightarrow g^1(\phi_a) = \phi_a, g^1(\phi_b) = \phi_b, g^1(\phi_c) = \phi_c, g^1(\phi_d) = \phi_d. \end{array}$$

Exercise. Complete the computations below.

Constant: $$\begin{array}{l} g_0(A) = A, g_0(B) = A, g_0(C) = A, g_0(D) = A \Rightarrow g^0(\phi_A) =?, \\ g_1(a) = 0, g_1(b) = 0, g_1c) = 0, g_1(d) = 0 \Rightarrow g^1(\phi_a) =?. \end{array}$$

Flip: $$\begin{array}{l} g_0(A) = D, g_0(B) = C, g_0(C) = B, g_0(D) = A \Rightarrow g^0(\phi_A) =?, \\ g_1(a) = c, g_1(b) = b, g_1(c) = a, g_1(d) = d \Rightarrow g^1(\phi_a) =?. \end{array}$$

Projection: $$\begin{array}{l} g_0(A) = A, g_0(B) = A, g_0(C) = D, g_0(D) = A \Rightarrow g^0(\phi_A) =? \\ g_1(a) = 0, g_1(b) = d, g_1(c) = 0, g_1(d) = d \Rightarrow g^1(\phi_a) =?. \end{array}$$

The cochain operator $g^k$ has similar results to those for the chain operator $g_k$. It's not surprising, after all its matrix is the transpose of $g_k$!

The cochain operator will be used to compute the cohomology operator $$g^* \colon H(L) \rightarrow H(K).$$