This site is being phased out.
Calculus 3: final
1. Find an equation of the plane through $(2,1,0)$ and parallel to \[x+4y-3z=1.\]
2. Express the length of the circle of radius $r$ as an arc length integral and evaluate it.
3. Find an equation of the tangent plane to the surface $z=4x^{2}-y^{2}+2y$ at the point $(-1,2,4).$
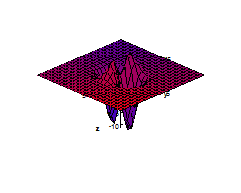
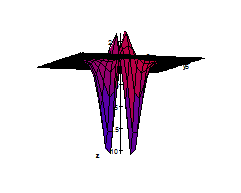
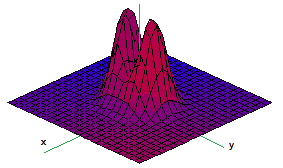
4. Make a sketch of contour (level) curves for the following function.
5. Find the directional derivative of the function $f(x,y)=1+2x\sqrt{y}$ at the point $(3,4)$ in the direction of the vector $<4,-1>$.%
6. Evaluate the double integral $\int\int_{D}(x+y)dA,$ where $D$ is bounded by $y=\sqrt{x}$ and $y=x^{2}$.
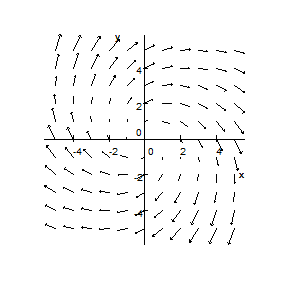
7. Vector field is sketched below. (a) Suppose $C$ is the positively oriented curve following the upper half of the unit circle. Is $\int _{C}\mathbf{F}\cdot d\mathbf{r}$ positive, negative or 0? Explain. (b) Suppose $P=(4,4).$ Is $div$ $F(P)$ positive, negative or 0? Explain.
8. Evaluate the line integral $\int_{C}x^{2}y^{3}dx-y\sqrt{x}dy$, where $C$ is parametrized by $x=t^{2},y=-t^{3},0\leq t\leq1.$
9. (a) Explain what it means for a line integral $\int_{C}\mathbf{F}\cdot d\mathbf{r}$ to be independent of path. (b) Is $\int_{C}\mathbf{F}\cdot d\mathbf{r},$ where $\mathbf{F}=<1-ye^{-x},e^{-x}>$ independent of path?
10. (a) State Green's Theorem. (b)Verify it for the vector field $\mathbf{F}(x,y)=y\mathbf{i}-x\mathbf{j}$ and a unit square.
11. Determine whether the vector field $F(x,y,z)=e^{z}\mathbf{i}% +\mathbf{j}+xe^{t}\mathbf{k}$ is conservative.
1. (a) Find the angle between the planes $x+y+z=1$ and $x-2y+3z=1$. (b) Find the equation of the line of intersection of these planes.
2. Find the equation of the line tangent to the curve $x=t^{5},y=t^{4},z=t^{3},$ at the point $(1,1,1).$
3. Find the curvature of the curve $<t^{2},t,5>$ as a function of $t.$
4. Make a sketch of contour (level)\ curves for the following function:
5. The wave heights $h$ in the open sea depend on the speed $v$ of the wind and the length of time $t$ that the wind has been blowing at that speed. Values of the function $h=f(v,t)$ are recorded in the table.
v\t 15 20 25 30 16 17 18 40 25 28 31 50 36 40 45
(a) Use the table to find a linear approximation to the wave function $f$ when $v$ is near 40 knots and $t$ is near 20 hours. (b) Estimate the wave heights when the wind has been blowing for 24 hours at 43 knots.
6. Find the dimensions of a rectangular box of maximal volume such that the total surface area is equal to 64.
7. Define the double integral of a function of two variables over a rectangle. Make a sketch and explain.
8. Find the volume of the tetrahedron bounded by the planes $x+2y+z=2,x=2y,x=0,$ and $z=0.$
9. Sketch the vector field $\mathbf{F}(x,y)=\dfrac{1}{\sqrt{x^{2}+y^{2}}}(y\mathbf{i}-x\mathbf{j}).$
10.Find the work done by force field $\mathbf{F}(x,y)=xy\mathbf{i}+y^{2}\mathbf{j}$ in moving an object along the parabola $x=t,y=t^{2},0\leq t\leq1.$
11. (a) Given a vector field $\mathbf{F}(x,y)=<3+2xy,x^{2}-3y^{2}>,$ find a function $f$ such that $\mathbf{\nabla}f=\mathbf{F}.$ (b) Use (a) to evaluate the line integral $\int_{C}\mathbf{F}\cdot d\mathbf{r},$ where $C$ is the curve given by $\mathbf{r}(t)=<e^{t}\sin t,e^{t}\cos t>,0<t<\pi.$
12. Verify Green's Theorem for the vector field $\mathbf{F}(x,y)=(x-y)\mathbf{i}+x\mathbf{j}$ and the region $D$ bounded by the unit circle $C:\mathbf{r}(t)=\cos t\mathbf{i}+\sin t\mathbf{j},0\leq t\leq2\pi.$