Affine function

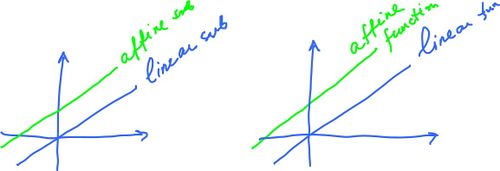
There is some confusion about the relation between linear and affine functions. In fact, in introductory calculus the term "affine" is never used. Everything with graph a straight line is a linear function.

Function f: ℝ → ℝ is a linear function only if has the form:

 f(x) = mx.

In other words, here each x is multiplied by the same number. That's a linear procedure! But mx + b is not.

Let's look at the properties of a function of this kind.

Addition is preserved under f:

 If f(x) = X and f(y) = Y, then f(x + y) = X + Y.

Here x + y is the input and X + Y is the output of f.

Let's instead consider

 f(x) = 3x + 1, 

then

 f(x + y) = 3(x + y) = 3x + 3y + 1;
 f(x) + f(y) = 3x + 1 + 3y + 1 = 3x + 3y + 2.

These functions are not equal! Thus 3x+1 does not preserve addition, so it’s not linear.

Scalar multiplication is preserved under f:

 If f(x) = X, then f(αx) = αX.

Instead consider

 f(x) = 3x + 1, 

then

 f(2x) = 3(2x) + 1 = 6x + 1;
 2f(x) = 2(3x + 1) = 6x + 2.

These functions are not equal!

Example. Consider

 f(x) = 3x + 1.

Addition is preserved if under f:

 x → X and y → Y ⇒ x + y  →  X + Y
   (input)   (output)

But:

 f(x + y) = 3(x + y) + 1 = 3x + 3y + 1
 f(x) + f(y) = 3x + 1 + 3y + 1 = 3x + 3y + 2 (the functions are not equal)

Thus, 3x + 1 does not preserve addition, so it is not linear.

Scalar multiplication is preserved if under f:

 x → X ⇒ αx → αX

But:

 f(2x) = 3(2x) + 1 = 6x + 1,  
 2f(x) = 2(3x + 1) = 6x + 2    (the functions are not equal).

more...