This site is being phased out.
Where do differential forms come from?
Suppose $I$ is a closed interval, such as $[a,b]$, then the (definite) integral of function $f$ over $I$ is understood as $$\int_I\color{maroon}{f(x)}dx.$$
In other words, the integral is simply a special kind of "parentheses" for function $f$, like this: $$G(f).$$ This approach is understandable as the Riemann integral is the limit of the Riemann sums of $f$. However, it's advantageous to look at this integral as $$\int_I\color{maroon}{f(x)dx}.$$ Then we can rewrite this as $$\int_I\color{maroon}{ω},$$ where $ω = f(x)dx$ is a differential form (of degree 1). The point is that the integral is now a function that is evaluated at ω, like this: $$H(ω) = \int_I ω.$$
Differential forms are also seen in calculus in "integration by substitution": $$u = x^2 => du = 2xdx.$$ The meaning of this computation is that the so-called exterior derivative of $0$-form (function $u$) is a $1$-form ($du$).
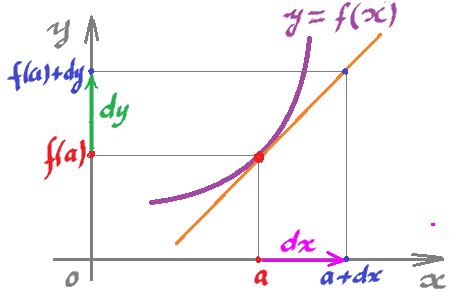
Differentials are $1$-forms:
When we solve a differential equation by "separation of variables", we are also using $1$-forms.
Differential forms of degree $2$ are seen too. The area integral of a function of $2$ variables over region $G$ on the plane is: $$V = \int_G\color{maroon}{f(x,y)dxdy}.$$
A line integral is an integral of a form of degree $1$. In dimension $2$, it looks like this: $$L = \int_C\color{maroon}{f(x,y)dx + g(x,y)dy}.$$
This approach produces one of the most beautiful formulas in the whole mathematics, the Stokes theorem: $$\int_ σ dω = \int_{∂σ} ω.$$ Here $σ$ is a cell (or more generally a chain) and $∂σ$ is its boundary.
Stokes theorem is a generalization of the Fundamental Theorem of Calculus. Indeed, it suffices to substitute this:
Differential forms also form a cochain complex which leads to a study of the topology of the underlying space via cohomology.
See also Discrete exterior calculus.