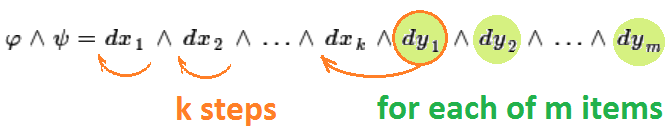This site is being phased out.
Wedge product of continuous forms
Redirect to:
Contents
$2$-forms as functions and as combinations $dx,dy$
Recall that we use
- location variables: $x,y,z$;
- direction variables: $v_x,v_y,v_z$, and possibly $v'_x,v'_y,v'_z$ etc.
We have defined the two "basis" $1$-forms: $$dx(x,y,v_x,v_y)=v_x,$$ $$dy(x,y,v_x,v_y)=v_y.$$ and the rest: $$\varphi^1=Adx+Bdy,$$ where $A=A(x,y),B=b(x,y)$ are functions.
Now $2$-forms.
They are $$\psi^2=Adxdy,$$ or in $3$-space $$\psi^2=Adxdy+Bdydz+Cdzdx,$$ i.e., "linear combinations" of forms $dxdy,dydz,dzdx$. Let's try to understand them.
The immediate idea is that $dxdy$ should be made of the basic $1$-forms we already understand, $dx,dy$. But how?
The first thought is that we just multiply them: $$dxdy=dx \cdot dy.$$ We can multiply two functions, so such a function makes sense.
Exercise. What kind of algebraic structure is $(\Omega ^1, +, \cdot)$?
However, this isn't what we want!
The fact that antisymmetry fails with $dx \cdot dy=dy \cdot dx$ springs to mind right away. But a bigger problem is that $dx \cdot dy$ is a $1$- not a $2$-form! Indeed we have: $$(dx \cdot dy)(x,y,v_x,v_y) = dx(x,y,v_x,v_y) \cdot dy(x,y,v_x,v_y),$$ or if we suppress locations $$(dx \cdot dy)(v_x,v_y) = dx(v_x,v_y) \cdot dy(v_x,v_y).$$
From this formula, it becomes clear that to produce a $2$-form from two $1$-forms, we shouldn't "recycle" the direction variables. We will need $$(dx \wedge dy)(v_x,v_y,v'_x,v'_y)=?$$
What should be the formula for the wedge product?
First, it has to be linear on $(v_x,v_y)$ and linear on $(v'_x,v'_y)$. The regular multiplication above works: $$dx(v_x,v_y) \cdot dy(v'_x,v'_y).$$ However, there is no antisymmetry! The answer is to flip the variables and then combine the results: $$(dx \wedge dy)(v_x,v_y,v'_x,v'_y) = dx(v_x,v_y) \cdot dy(v'_x,v'_y) - dx(v'_x,v'_y) \cdot dy(v_x,v_y).$$ This suggests that in any dimension, we have: $$(\varphi ^1 \wedge \psi ^1)(v,v')= \varphi ^1(v) \cdot \psi ^1(v') - \varphi ^1(v') \cdot \psi ^1(v).$$
So, the explicit formula of our new form is: $$(dxdy)(x,y,v_x,v_y,v'_x,v'_y) = v_xv'_y - v_yv'_x.$$ Of course, we recognize this as a determinant.
We have found a way to construct the "familiar" $2$-form named $dxdy$ from the two "familiar" (and explicitly defined) $1$-forms named $dx$ and $dy$. Now we need to extend this construction to all forms.
Now, for the $2$-dimensional space we've got all we need. All $2$-forms are given by: $$\psi^2=Adx \wedge dy = Adxdy.$$
In $3$-space it's more complicated: $$\psi^2=Adxdy+Bdydz+Cdxdz,$$ where these three $2$-forms form a basis and can be constructed from the familiar $1$-forms $dx,dy,dz$ via the wedge product.
Let's use the above properties to simplify products of forms.
Example. Simplify the product $$(x^2 dx + xydy + dz) \wedge (x dxdy + zdxdz).$$ We proceed by carrying out the multiplication according to the multilinearity (which looks like the familiar distributive property of algebra): $$x^2 dx \wedge x \wedge dxdy + x \wedge y \wedge dy \wedge x \wedge dxdy + dz \wedge x \wedge dxdy + x^2 \wedge dx \wedge z \wedge dxdz + xy \wedge dy \wedge z \wedge dxdz + dz \wedge z dxdz.$$
In the first term, $x^2 dx \wedge x \wedge dxdy$, the factor $x$ is a coefficient of the $1$-form $dxdy$, and by multilinearity, it goes to the front to yield the term $x^3 dxdxdy$. We apply similar rules to the other terms of this product and we get a linear combination of the familiar $3$-forms: $$x^3 dxdxdy + x^2ydydxdy + xdzdxdy + x^2z dxdxdz + xyz dydxdz + z dzdxdz.$$ We can arrange these terms by antisymmetry to get the following formula: $$x^3 dxdxdy - x^2ydydydx - xdxdydz + x^2z dxdxdz - xyz dxdydz - z dzdzdx.$$ Now by the Corollary above, the first, second, fourth, and last terms must equal zero leaving us with $$x dxdydz - xyz dxdydz = (x - xyz) dxdydz.$$
The notation $\varphi \wedge \psi$ is common but we simply omit all symbols when the context is clear, as in $\varphi \psi$ and especially $dxdy$.
The wedge product
We have defined the wedge product on $dx,dy$ (and $dz$ in the $3$-space) and the last example suggest how one can apply it to all forms.
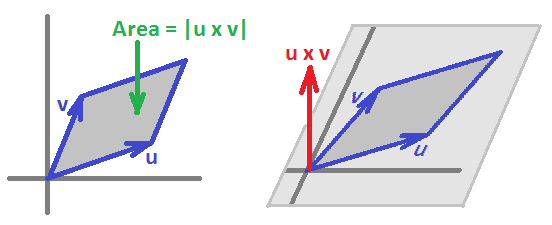
Generally, we use the fact that those two form a basis of $\Omega^1({\bf R}^2)$ and we also require the wedge product, $$\wedge \colon \Omega^1 \times \Omega^1 \rightarrow \Omega^{2},$$ to be linear on each of the multiples. Then $$\varphi^1\wedge\psi^1=(Adx+Bdy)\wedge(Cdx+Ddy)$$ $$=(Adx)\wedge (Cdx)+(Adx)\wedge (Ddy)+(Bdy)\wedge (Cdx)+(Bdy)\wedge (Ddy)$$ Use the linearity of the wedge product: $$=ACdx\wedge dx+ADdx\wedge dy+BCdy\wedge dx+BDdy\wedge Ddy$$ $$=ACdxdx+ADdxdy+BCdydx+BDdydy$$ Use the antisymmetry $$=AC0+ADdxdy+BCdydx+BD0$$ $$=(AD-BC)dxdy.$$ It is interesting to notice that this is equal to a certain determinant: $$AD-BC=\det \left( \begin{array}{ccc} A & B \\ C & D \end{array} \right). $$ This number also represents the area of the parallelogram spanned by vectors $u=<A,B>,v=<C,D>$ in the plane:
One can think of it as the cross product of these vectors. This idea is also visible in dimension $3$: $$\varphi^1\wedge\psi^1=(Adx+Bdy+Cdy)\wedge(Ddx+Edy+Fdz).$$ We just quickly collect the similar terms here while dropping zeros: $$=(AE-BD)dxdy$$ $$+(BF-CE)dydz$$ $$+(AF-CD)dxdz,$$ which is almost the same as $$u \times v = <A,B,C> \times <D,E,F> = \det \left( \begin{array}{ccc} i & j & k \\ A & B & C \\ D & E & F \end{array} \right) $$ Even though this connection is important, the real insight comes from "exterior algebra".
The idea is to study vectors, such as $u$ and $v$, as well "$2$-vectors", such as $u \wedge v$, which is simply $u$ and $v$ paired up, and "$3$-vectors" $u \wedge v \wedge w$, etc. The properties that we have seen are required from these "multi-vectors". For example, the $2$-vectors should be linear on either vector and and be anti-symmetric.
Then $k$-vectors capture the oriented $k$-volumes:
- lengths are linear,
- areas are bi-linear,
- volumes are tri-linear, etc,
just as above. Warning: This is not about the arc-length, surface area, etc from calculus, which are independent of orientation.
In the $3$-dimensional case each $2$-vector $u \wedge v$ corresponds to a regular vector $u \times v$ and that explains the connection discussed above. In the general case the connection breaks down.
With this insight, the combined direction variable of a $k$-form is a $k$-vector.
Back to the wedge product of forms.
We already have an idea that this operator behaves as follows: $$\wedge \colon \Omega^k \times \Omega^m \rightarrow \Omega^{k+m},$$ that is, multiplication of lower dimensional forms yields higher dimensional forms.
We build this operator inductively.
We already understand the wedge product for the degree $1$ forms in all dimensions. For dimension $3$ the construction for all forms can be easily outlined. First we list the bases of the spaces of differential forms of each degree:
- $\Omega ^0({\bf R}^3) : \{1\}$;
- $\Omega ^1({\bf R}^3) : \{dx,dy,dz\}$;
- $\Omega ^2({\bf R}^3) : \{dxdy,dydz,dxdz\}$;
- $\Omega ^3({\bf R}^3) : \{dxdydz\}$;
- $\Omega ^k({\bf R}^3) =0$ for $k>3$.
Next we define the wedge product as a linear operator (on each multiple) $$\wedge \colon \Omega^k({\bf R}^3) \times \Omega^m({\bf R}^3) \rightarrow \Omega^{k+m}({\bf R}^3)$$ in the usual way. For each pair of the basis elements of the domain spaces we express their wedge product in terms of the basis of the target space. For example:
- $\wedge \colon \Omega^0 \times \Omega^1 \rightarrow \Omega^{1}$
- $\wedge(1,dx)=1 \wedge dx =dx, \wedge(1,dy)=1 \wedge dy =dy, \wedge(1,dz)=1 \wedge dz =dz$;
- $\wedge \colon \Omega^1 \times \Omega^1 \rightarrow \Omega^{2}$
- $\wedge(dx,dy)=dx \wedge dy =dxdy,\wedge(dy,dz)=dy \wedge dz =dydz,\wedge(dx,dz)=dx \wedge dz =dxdz$;
- $\wedge(dy,dx)=dy \wedge dx =-dxdy,\wedge(dz,dy)=dz \wedge dy =-dydz,\wedge(dz,dx)=dz \wedge dx =-dxdz$;
- $\wedge(dx,dx)=dx \wedge dx =0,\wedge(dy,dy)=dy \wedge dy =0,\wedge(dz,dz)=dz \wedge dz =0$.
- etc
By analogy with linear algebra, we conclude that these conditions fully define $\wedge$ as a linear operator.
Clearly, these spaces aren't closed under the wedge product which is what we are used to. To make it a "self-map" we use a graded vector space: $$\wedge \colon \Omega^0 \times \Omega^1 \times \Omega^2 \times \ldots \rightarrow \Omega^0 \times \Omega^1 \times \Omega^2 \times \ldots.$$ Observe that this approach also allows adding any two forms not just ones of the same degree.
The wedge profuct is associative. Indeed, using $dd=0$ and antisymmetry, we compute: $$\Big[(Adx+Bdy+Cdz) \wedge (Edx+Fdy+Gdz)\Big] \wedge (Hdx+Idy+Jdz) $$ $$=(BGH-CFH)dxdydz + (CEI-AGI)dxdydz + (AFJ-BEJ)dxdydz.$$ and $$(Adx+Bdy+Cdz) \wedge \Big[(Edx+Fdy+Gdz) \wedge (Hdx+Idy+Jdz)\Big] $$ $$= (AFJ-AGI)dxdydz + (BGH-BEJ)dxdydz + (CEI-CFH)dxdydz.$$
We will refer to the forms $dx,dy,dx,dxdy$ etc and $dx^{i_1} \wedge ... \wedge dx^{i_k}$ as the basic forms. As all forms appear to be "linear combinations" of these, such a term makes sense. However, the coefficients in these linear combinations are functions, therefore we can't think of these forms as a basis of $\Omega ^k$ -- as a vector space that is. The reason is that the operations of vector spaces involve coefficients in a field and the space of functions isn't a field. An analogue of a vector space with coefficients in a ring is called a module. It is beneficial sometimes to look at $\Omega ^k$ as a module and, in this case, the basic forms do provide its basis. Unfortunately, if we adopt this point of view, the derivative (and the exterior derivative $d:\Omega ^k \rightarrow \Omega ^{k+1}$) isn't a linear operator anymore!
Skew commutativity
Is the wedge product commutative?
No, because we know that $dx \wedge dy= -dy \wedge dx$.
Is the wedge product anti-commutative?
No, once we realize that $f^0 \wedge \varphi = f^0\varphi$ is simply multiplication.
Example. Consider the product $dx \hspace{1pt} dy \hspace{1pt} dz$. By antisymmetry we have $$dx \hspace{1pt} dy \hspace{1pt} dz = -dy \hspace{1pt} dx \hspace{1pt} dz = dy \hspace{1pt} dz \hspace{1pt} dx,$$ so it seems that $$dx \hspace{1pt} (dy \hspace{1pt} dz) = (dy \hspace{1pt} dz) \hspace{1pt} dx,$$ which suggests that multiplication of forms may be commutative. However consider in ${\bf R}^4$ the product $$dx \hspace{1pt} dy \hspace{1pt} dz \hspace{1pt} du = -dy \hspace{1pt} dx \hspace{1pt} dz \hspace{1pt} du = dy \hspace{1pt} dz \hspace{1pt} dx \hspace{1pt} du = -dy \hspace{1pt} dz \hspace{1pt} du \hspace{1pt} dx.$$ So we cannot say in general that multiplication of forms is a commutative operation.
So the answer is, it depends on the degrees of the forms.
It is clear now that we can rearrange the order of the multiples step by step and every time the only thing that changes is the sign. Then there must be a general rule here: $$\varphi \wedge \psi = (-1)^{?}\psi \wedge \varphi.$$ What is the sign? It depends only on the number of flips we need to do.
All we know is that, if $\varphi \in \Omega^k$ and $\psi \in \Omega^m$, then $\varphi \wedge \psi$ is an $(m+k)$-form.
Example. Let $\varphi = dx \hspace{1pt} dy$ and $\psi = dz \hspace{1pt} du$. Then $$\varphi \wedge \psi = dx \hspace{1pt} dy \hspace{1pt} dz \hspace{1pt} du = dz \hspace{1pt} du \hspace{1pt} dx \hspace{1pt} dy.$$ To understand the sign, we observe that we simply count the number of times we move an item one step left (or right) and use the anti-symmetry property: $$(dxdy)(dzdu)=(-1)^?(dzdu)(dxdy).$$
This suggests that the property might look like this: $$\varphi \wedge \psi = (-1)^4 \psi \wedge \varphi .$$
Indeed, there is a more general result here.
Theorem: Suppose $\varphi \in \Omega^k$ and $\psi \in \Omega^m$. Then $$\varphi \wedge \psi = (-1)^{km}\psi \wedge \varphi.$$
Proof: We use linearity to reduce the problem to that for $\varphi = dx_1 \hspace{1pt} dx_2\ldots dx_k$ and $\psi = dy_1 \hspace{1pt} dy_2\ldots dy_m$. Then our product is $$\varphi \wedge \psi=(dx_1 \hspace{1pt} dx_2\ldots dx_k) \wedge (dy_1 \hspace{1pt} dy_2\ldots dy_m).$$ To move $dy_1$ to the left of $dx_1$ requires precisely $k$ jumps -- and as many applications of the anti-symmetry property (of the wedge product of $1$-forms) to this expression: $$\varphi \wedge \psi=dx_1 \hspace{1pt}\wedge \hspace{1pt} dx_2 \hspace{1pt} \wedge \hspace{1pt}\ldots \wedge \hspace{1pt} dx_k \hspace{1pt}\wedge \hspace{1pt} dy_1 \hspace{1pt}\wedge \hspace{1pt} dy_2\wedge \hspace{1pt}\ldots \wedge \hspace{1pt}dy_m$$ as follows
So, we get a factor of $(-1)^k$ by moving $dy_1$. Then, moving $dy_2$ also requires precisely $k$ steps, so our factor becomes $(-1)^k(-1)^k=(-1)^{2k}$. We perform this jumping for each of the $m$ of the $dy_i$ factors which yields the factor $(-1)^{km}$. $\blacksquare$
This property is called skew commutativity.
Corollary: If $\varphi \in \Omega^k$ and $k$ is odd, then $\varphi \wedge \varphi = 0$.
Proof. Exercise.
We have proven that each of these two properties implies the other:
See also cup product.
Exercises
1. Compute
- (a) $x^2dx^1$ on $<1,2,3>$ at $(3,2,1)$;
- (b) $dx^1 \wedge dx^3 + x^1dx^2 \wedge dx^4$ on the pair $<-1,0,1,1>, <0,-1,0,1>$ at $ (1,0,0,0)$;
2. Simplify: $$2dx^1 \wedge dx^3 \wedge dx^2 + 3dx^2 \wedge dx^1 \wedge dx^2 - dx^2 \wedge dx^3 \wedge dx^1 .$$
3. Expand and simplify: $$(x^1 dx^2 + x^2 dx^1) \wedge (x^3 dx^1 \wedge dx^2 + x^2 dx^1 \wedge dx^3 + x^1 dx^2 \wedge dx^3).$$
4. Show that a form of even degree commutes with any other form.
5. $\dim \Omega ^k (p) = ?$
6. Provide explicit formulas of the basic forms in $\Omega ^2({\bf R}^3)$, i.e., $dxdy,dydz,dzdx$ in terms of the axiomatic definition. Suggest a formula for the general case of $\Omega ^k({\bf R}^n)$.