Vector spaces: introduction

We start with...

Real numbers and their algebra

We will make observations -- about numbers -- and extract more specific properties, i.e., theorems about numbers, from these observations. Finally, we forget about numbers and treat these theorems as axioms -- about algebraic entities more general than just numbers.

Example...

Where does this algebra:

• $x+2x=3x$

come from? It comes from arithmetic, observations like this:

• $5+2\cdot 5=3\cdot 5$.

This observation suggests the distributive property of numbers:

• $a(b+c)=ab+ac$.

Let's try it

• $ab+ac = x + 2x$ let $a=x$, $b=1$, $c=2$.

Then

• $ab + ac = x \cdot 1 + x \cdot 2 = x + 2x$.

Turns out we used more than that here. We also used the multiplicative identity:

• $1 \cdot d = d \rightarrow d \cdot 1 = d$.

Only now we apply distributive property:

• $x + 2x = x \cdot 1 + x \cdot 2 = x(1+3) = x \cdot 3 = 3x$.

Other properties:

• Multiplicative commutativity: $ef = fe$
• Associativity: $a + (b+c) = (a+b)+c$ and $a \cdot (b \cdot c) = a \cdot (b \cdot c)$
• Additive identity: $0+a=a+0=a$.

Why isn't on the list?

• $0\cdot a = 0$

Because it's not independent from the rest (and we want to make the set of axioms as short as possible). Indeed we derive it:

• $0a = (0+0)a=0a+0a$, next $0a-0a=0a+0a-0a$, therefore $0=0a$.

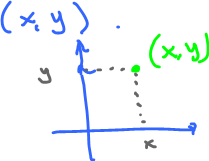
The first entity that satisfies the axioms that we discover is ordered pairs of numbers $(x,y)$, i.e., 2-vectors. Geometrically, they are points on the plane:

But that's not important, algebraically! The point is that we can perform some algebraic operations with these entities if we define them properly.

Definition: Define "addition":

• $(x,y) + (a,b) = (x+a, y+b)$.

Exercise. Verify the properties (aka axioms).

What axioms for this can we get from the axioms of real numbers? The following three axioms have analogues.

Associativity for $2$-vectors:

$\begin{align*} ((x,y)+(a,b))+(u,v) &\stackrel{ {\rm def} }{=} (x+a,y+b)+(u,v) \\ &\stackrel{ {\rm def} }{=} ((x+a)+u, (y+b)+v) \\ &\stackrel{ {\rm assoc. \hspace{3pt} twice} }{=} (x+(a+u), y+(b+v)) \\ &\stackrel{ {\rm def} }{=} (x,y)+(a+u,b+v) \\ &\stackrel{ {\rm def} }{=} (x,y)+ ((a,b)+(u,v)) \end{align*}$

What about $3$-vectors $(x,y,z)$, or $n$-vectors $(x_1,\ldots,x_n)$?

Same.

More compact rule (associativity for vectors):

• $(X+A)+U=X+(A+U)$, where $X=(x,y)$, $A=(a,b)$, and $U=(u,v)$.

Note: Often vectors are bold: ${\bf v}$. Elsewhere, they have an arrow: $\vec{v}$ . We don't use this notation here. From context, it should be clear when this is a vector.

What about multiplication?

• $(x,y)(a,b)=(xa,yb)$.

It doesn't make as much sense...

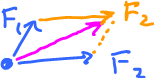
Vectors come from physics, velocities, forces, etc.

$F_1+F_2$ is geometric addition.

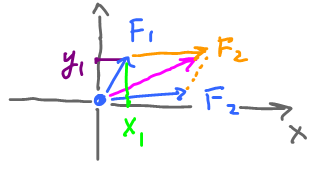
$F_1+F_2$ is geometric addition with a coordinate system. In this case, forces are pairs of numbers $F_1=(x_1,y_1)$, where $x_1$ is called the $x$-component and $y_1$ is called the $y$-component.

The physics approach gives us this idea about vectors:

• ${\rm vector} = {\rm magnitude} \& {\rm direction}$.

Exercise: Prove this:

• $F_1+F_2 = (x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$

To have the algebra of vectors, what else do we need to handle the physics?

What if I want to double the force?

• Geometry: Same direction, twice the magnitude.
• Algebra: Multiply both components by $2$:

$$2(x,y)=(2x,2y)$$ (on the left hand side, the $2$ is a number and $(x,y)$ is a vector).

This is called scalar multiplication, also known as "scalar product": $${\rm number} \cdot {\rm vector}.$$

Exercise: $r(x,y) = (rx,ry)$ is coordinate-wise scalar multiplication.

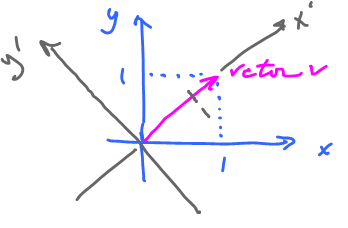
It's important to remember that pairs of numbers are vectors but vice versa isn't as clear-cut: vectors are converted to pairs differently for each coordinate system chosen.

Let's start with $v=(1,1)$, in the standard system.

Now what if we have another system? Let's try $(x',y')$. Then $v=(\sqrt{2},0)$.

Important point: We want algebra independent from the coordinate system.

Hence our

Coordinate free approach

Definition: A vector space is a set $V$, where two operations are defined:

• addition: $u,v \in V$ then $u+v \in V$,
• scalar multiplication: $r \in {\bf R}$, $u \in V$, then $ru \in V$

(notice multiplication is on the left!).

They satisfy the conditions: for all $u,v,w \in V$, $r,s \in {\bf R}$

• 1. $u+v = v+u$ (commutativity of addition)
• 2. $(u+v)+w = u+(v+w)$ (associativity of addition)
• 3. There is a vector $0 \in V$ such that $0+a=a$ for all $a \in V$ (additive identity)
• 4. For each $a \in V$ there is a vector $-a \in V$ such that $a + (-a) = 0$ (additive inverse)

(note: $-a$ is simply a special name here.)

• 5. $r(u+v)=ru+rv$ (first distributive law)
• 6. $(r+s)u=ru+su$ (second distributive law)
• 7. $(rs)u=r(su)$ (associative law for scalar multiplication)

(note: $rsu$ does not make sense before the previous law)

• 8. $1u = u$ (multiplicative identity)

No subtraction, no cancellation; they come later.

Main idea: A vector space is "closed" under these operations.

To illustrate:

Example: ${\bf Z}$, the integers, is not a vector space, because it is not closed under scalar multiplication. Consider

• $\frac{1}{2} \cdot 3 = \frac{3}{2} \not\in {\bf Z}$.

Consider also: $${\bf R}, {\bf C}, {\bf Q}, {\bf Z}_2.$$

Example: ${\bf Z}_2 = \{0,1\}$ is not closed under addition, but is closed under multiplication. (Wait for Modern algebra: course.)

Example: $(0,\infty)$ is closed under addition, but...

What more do we need? What follows from the axioms?

Special vectors...

• #3. $0$ is a vector. How many are there?

Let's prove it's unique. How?

Suppose there are two, another one called $0'$. Both satisfy #3. Need to show $0=0'$.

By #3, $0+0' = 0'$ and $0' + 0 = 0$, same by #1, implying $0=0'$. Done.

• #4. Similar. Given $a \in V$, is a unique? Yes. Exercise.

Proposition:

• $0v=0$

(on the left side $0$ is a number and $v$ is a vector).

Observe: this is not an axiom!

We can continue on and on... More and more corollaries. Too many to learn them all.

Proposition:

• $r0=0$

(this will justify using: the zero vector).

Try to prove some of these. Rely only on axioms.

Define subtraction and cancellation. Prove some properties.

Proposition: $v-0=v$

$\frac{v}{3}=\frac{1}{3}v$

Specific vector spaces:

• Numbers: ${\bf R}, {\bf C}, {\bf Q}, {\bf Z}_2$ \\

But the main example is...

Euclidian spaces

$\begin{align*} {\bf 0} & \{0\} \\ {\bf R} & {\rm real \hspace{3pt} numbers} \\ {\bf R}^2 & {\rm spaces \hspace{3pt} of \hspace{3pt} pairs \hspace{3pt}} (x,y) {\rm with \hspace{3pt} operations \hspace{3pt}} \\ & & (x,y)+(a,b)=(x+a,y+b); r(x,y)=(rx,ry) \\ {\bf R}^3 & {\rm space \hspace{3pt} of \hspace{3pt} tuples \hspace{3pt}} (x,y,z) \\ \vdots & & \\ {\bf R}^n & (x_1,x_2,\ldots,x_n), x_i \in {\bf R} \end{align*}$

Trick question: Is $\emptyset$ a vector space?

No. Why? It does not satisfy #3: $0 \in V$

Operations:

• $(x_1,x_2,\ldots,x_n)+(a_1,a_2,\ldots,a_n) = (x_1+a_1,x_2+a_2,\ldots,x_n+a_n)$ and
• $r(x_1,x_2,\ldots,x_n) = (rx_1,rx_2,\ldots,rx_n)$.

Verify the axioms. How? Coordinate-wise and component-wise.

Here $v$ is a vector and $x,y,z$ are its "components".

Example: Commutativity for numbers $x+y=y+x$ we know, then commutativity for vectors follows. Same for associativity.

What about #3? What is $0$ in ${\bf R}^n$?

• $0 = (0,0,\ldots,0)$

What about #4? What's $-v$ in ${\bf R}^n$?

• If $v=(x_1,\ldots,x_n)$, then $-v=(-x_1,\ldots,-x_n)$.

Generally, $${\bf R}^n = \{ (x_1,\ldots,x_n) \colon x_i \in {\bf R}, i=1,\ldots,n\}.$$

What about ${\bf R}^{\infty}$?

Is there such a thing? Yes.

$${\bf R}^{\infty} = \{(x_1,\ldots,x_n,\ldots) \colon x_i \in {\bf R}, i=1,2,\ldots \}$$

So, ${\bf R}^{\infty}$ consists of infinite sequences and is not Euclidean.

Can we make this set into a vector space?

How do we define operations?

• $(x_1,x_2,\ldots)+(a_1,a_2,\ldots) = (x_1+a_1,x_2+a_2,\ldots)$ and
• $r(x_1,x_2,\ldots) = (rx_1,rx_2,\ldots)$.

Axioms work out OK (check them all component-wise).

Back to ${\bf R}^2$.

This is the plane, but also space of pairs $\{(x,y) \colon x,y \in {\bf R}\}$.

What else?

Consider

Systems of linear equations

Specifically, $2$ equations and $2$ unknowns: $$\left\{ \begin{array}{rl} x+y=0 \\ x-y=0 \end{array} \right.$$ Substitution solves it.

Note: we deal with homogeneous systems, i.e.m $0$'s for the right hand side.

$\left\{ \begin{array}{rl} x+y=0 \\ x-y=0 \end{array} \right.$ $\rightarrow x=0, y=0 \rightarrow \{(0,0)\} \subset {\bf R}^2$

Interpret the answer in ${\bf R}^2$. $(x,y) \in {\bf R}^2$: the two equations are straight lines and the solution is their intersection.

It's been ${\bf R}^2, \{(0,0)\}$ so far. Now we can create more.

Define $$V=\{(x,y) \in {\bf R}^2 \colon x+y=0\}.$$ This is a vector space!

Observe: $u+v \in V$ and $ru \in V$. Comes from a geometric idea...

Let's prove this algebraically.

Given $(x,y) \in V$, $(a,b) \in V$, we have $x+y=0$ and $a+b=0$ (*).

Is it true $(x,y)+(a,b)=(x+a,y+b) \in V$?

We need to show $(x+a)+(y+b)=0$. Easy. Assuming the axioms work,

$$\begin{align*} (x,y)+(a,b) &\stackrel{{\rm by \hspace{3pt} (*)}}{=} (x+y)+(a+b) \\ &= 0+0 \\ &= 0 \end{align*}$$

Also, $W=\{(x,y) \in {\bf R}^2 \colon x-y=0\}$ is a vector space. And $V \cap W = 0$ is also a vector space.

Observation: A solution set $(x,y)$ in ${\bf R}^2$ of a homogeneous linear equation is a vector space.

Same for systems of equations.

Example. Is $Y = \{(x,y) \colon x \geq 0\}$ a vector space?

No.

Why: $(1,0) \in V$ but $-(1,0) = (-1,0) \not \in V$.

Matrices

An $n \times m$ matrix is a table of real numbers with $n$ rows and $m$ columns.

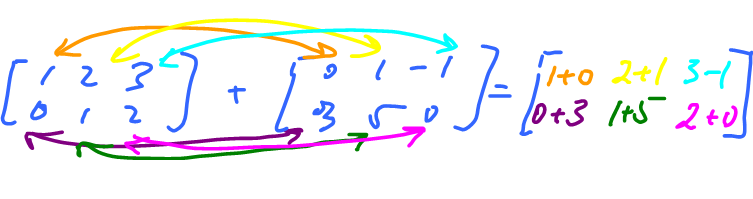
Example: For $n=2$ and $m=3$, we can look at:

That's matrix addition: $\left[ \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 1 & 2 \end{array} \right] + \left[ \begin{array}{ccc} 0 & 1 & -1 \\ 3 & 5 & 0 \end{array} \right] = \left[ \begin{array}{ccc} 1+0 & 2+1 & 3-1 \\ 0+3 & 1+5 & 2+0 \end{array} \right]$

where the right hand side comes from matching the elements in both matrices with the sign $+$.

And this is how we multiply a matrix by a number:

$3\left[ \begin{array}{ccc} 0 & 1 & 2 \\ 5 & 1 & 3 \end{array} \right] = \left[ \begin{array}{ccc} 3 \cdot 0 & 3 \cdot 1 & 3 \cdot 2 \\ 3 \cdot 5 & 3 \cdot 1 & 3 \cdot 3 \end{array} \right]$

Exercise: Consider the following operations on ${\bf R}^2$:

• $(x,y)+(a,b)=(x+1,y+b+1)$,
• $r(x,y)=(rx,ry)$.

Axioms:

• #1. commutativity $\checkmark$
• #2. associativity $\checkmark$
• #3. additive identity $0=(0,-1) \checkmark$
• #4. additive inverse $?$

Given $v=(x,y)$, is there $-v$ such that $v + (-v)=0$?

Say $-v=(a,b)$. Find these $(x,y)+(a,b)=(0,-1)$, or $(x+a, y+b+1)=(0,-1)$. This is a vector equation. (In this case, $x$ and $y$ are known and $a$ and $b$ are unknown.)

Rewrite coordinate-wise:

$\left\{ \begin{array}{rl} x+a=0 \\ x+b+1=-1 \end{array} \right.$

Solve it: $a=-x$ and $b=-2-y$.

So what? It passes #4. $\checkmark$.

• #5. distributive law

$\begin{align*} r(u+w) &=r((x,y)+(a,b) \\ &=r(x+a,y+b+1) \\ &=(rx+ra,ry+rb+r) \end{align*}$

$\begin{align*} rx+rw &= r(x,y)+r(a,b) \\ &= (rx,ry)+(ra,rb) \\ &= (rx+ra,ry+rb+1) \end{align*}$

Notice there is no match if $r\ne 1$. Therefore #5. fails. $\blacksquare$

Matrices, continued.

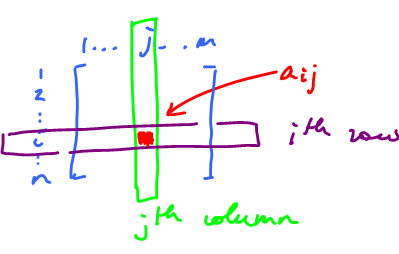
An $n \times m$ matrix has $n$ rows and $m$ columns. Notation: $M(n,m)$ is the set of these matrices.

Typically, we use $A$ (capital) for matrix, and $A=\{a_{ij}\}$ is the entry of $A$ at the $i^{\rm th}$ row and $j^{\rm th}$.

Example: $A = \left[ \begin{array}{ccc} 1 & 2 \\ 0 & 3 \end{array} \right]$ then $a_{11}=1$, $a_{12}=2$, $a_{21}=0$, $a_{22}=3$.

Example: $A=\{ a_{ij} \}$, $100 \times 100$, $a_{ij}=i+j$.

The idea behind this notation is like the one behind sequences: $a_n=n^2$ (Calculus 2: course).

Except now we have two subscripts:

$$B=\{b_{ij}\}, 100 \times 100, b_{ij}=i-j+1.$$

Then $A+B=C=\{c_{ij}\}$, where

$\begin{align*} c_{ij} &=a_{ij}+b_{ij} \\ &= i+j+i-j+1 \\ &= 2i+1. \end{align*}$

Proposition: $M(n,m)$ is a vector space with these operations:

• $\{a_{ij}\} + \{b_{ij}\} = \{a_{ij} + b_{ij} \}$
• $r\{a_{ij}\} = \{ra_{ij}\}$

Exercise: What is the connection between $M(n,m)$ and ${\bf R}^k$? $$M(n,m) \longleftrightarrow {\bf R}^k$$

Simple: turn a matrix into a vector:

$\left[ \begin{array}{ccc} 1 & 2 \\ 3 & 4 \end{array} \right] \rightarrow (1,2,3,4)$,

We flatten a table into a string:

What is $k$? $k=nm$.

Exercise: Verify the axioms.

Example: $V = \{A \in M(2,2) \colon a_{11}+a_{12}-a_{21}-a_{22}=0\}$ is a vector space.

$W = \{A \in M(2,2) \colon a_{11}+a_{12}-a_{21}-a_{22}=1\}$ is not a vector space!

Also $U=\{A \in M(2,2) \colon a_{11}^2+a_{12}-a_{21}-a_{22}=0\}$ is not a vector space.

Example: $M(1,m)$ "=" ${\bf R}^m$ in what sense?

$(a_{11},\ldots,a_{1m}) \stackrel{?}{=} (a_1,\ldots,a_m)$, just a string of numbers. Plus, the operations are the same.

Also, $M(n,1)={\bf R}^n$:

$\left[ \begin{array}{ccc} a_{11} \\ a_{21} \\ \vdots \\ a_{n1} \end{array} \right]^T \rightarrow [a_1,\ldots,a_n]$ by "transposition".

Definition: If the elements are flipped about the main diagonal the new matrix is called the transposition. Algebraically, $\{a_{ij}\}^T = \{a_{ji}\}$.