This site is being phased out.
Student's guide to proof writing
These are 10 rules (or tests, or clues) that you can use to check if there may be problems with what you are about to submit...
Once upon a time a lecture was being given:
Pythagorean Theorem: $a^2+b^2=c^2$ for the sides of a right triangle...
Homework assignment: Prove the theorem.
.
.
Law of Cosines: $a^2+b^2-2ab\cos \alpha=c^2$ for the sides of a triangle with angle $\alpha$...
The week after this was submitted:
Homework solution: To prove the Pythagorean Theorem, take the Law of Cosines and set $\alpha = 90$ degrees, done.
What is wrong with this picture?
The argument is circular as the proof of the Law of Cosines is (usually) based on the Pythagorean Theorem. That's why the lectures that follow the assignment should be off-limits.
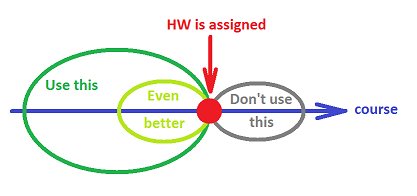
Rule 1: If you use in your proof results presented in lectures after the homework was assigned, this is very likely not what's expected from you.
To check all the lectures may be impossible, and the purpose of the rule is to eliminate any chance of circular reasoning.
The version of this rule for the professor to follow: Don't assign homework until all the necessary material has been covered.
The example provides a rationale for the following:
Rule 2: If your proof is "The statement is just a particular case of this theorem", that's probably not what's expected from you.
Be especially careful if this theorem comes from outside the course. Simply put, a very short proof generally is a bad sign. This rule is meant to prevent you from being tempted by an easy way out. A proof from scratch -- based on the concepts being discussed in the class you are taking -- is expected just about every single time.
To summarize the two rules: the proof should be as localized as possible, but only on one side (think $(a-\epsilon,a]$).
Rule 3: If your proof doesn't provide the definition or quote a theorem for each concept used, it is probably flawed.
The danger is that the proof is superficial and hand-wavy.
A proof that looks like an essay can probably use a lot more structure.
Rule 4: If your proof is long but has no lemmas, it is likely to be flawed.
It is certainly not very readable. It is not readable for the professor but for you too -- that's why there is a chance it may have problems that you've overlooked.
Note: In just about any undergraduate or graduate course a one-page proof in TeX (with no illustrations) is long.
The rule doesn't mean to proclaim that long is bad. Just the opposite is true: one shouldn't keep any part of the proof for himself.
Rule 5: If you have an “easy” part of the proof in your head but don't put it on paper, this part is likely to be challenged.
Rule 6: If you don't introduce all or most of the objects in the proof by giving them letter names, your proof may be flawed.
The danger is again that the proof is superficial and hand-wavy. Always start with "Let $x$ be..."
Note: How to choose good notation is a subject of a separate discussion.
Rule 7: If you introduce an object in your proof and then never use it, this is a problem and might be a sign of other problems.
That would leave a very bad impression...
Rule 8: If you don't use all of the conditions of the theorem you are to prove, your proof is very likely to be flawed.
You simply don't see a lot of theorems with redundant conditions.
Your drawings may fool you. In fact, draw a triangle...
Now, take a closer look at it; you are likely to discover that your triangle is either a right triangle or an isosceles. A proof based on this picture could easily be flawed.
Rule 9: If removing all pictures from your proof makes it incomplete or just hard to follow, it is probably not rigorous enough.
Let illustrations illustrate...
And finally, just because your professor or your textbook violate, as they often do, some or all of these rules, don't assume that you are off the hook.
Rule 10: If you write your proof as just a variation of a proof taken from a lecture or a book, it is likely that higher standards will be applied to yours.