Simply connected spaces

Question:

• Can you can get from $A$ to $B$ in two (topologically) different ways?

Another way to understand the question: any closed curve can be "contracted" to point, without leaving the set. For example a circle does not satisfy this condition.

So, $X$ is called simply connected if every closed curve can be "contracted" -- via homotopy -- to a point without leaving $X$:

Exercise: Verify whether the following sets are simply connected:

• disk $\{(x,y) \in R^2:x^2+y^2<1\}$;
• circle with pinched center $\{(x,y) \in R^2:0<x^2+y^2<1\}$;
• ball with pinched center $\{(x,y,z) \in R^3:0<x^2+y^2+z^2<1\}$;
• ring $\{(x,y) \in R^2:1/2<x^2+y^2<1\}$;
• thick sphere $\{(x,y,z) \in R^3:1/2<x^2+y^2+z^2<1\}$;
• the donut.

The importance of the concept can be seen in calculus, as follows.

Recall a vector field is a function $f: {\bf R}^2 \rightarrow {\bf R}^2$. It is called conservative if it is a gradient of a scalar function: $F = {\bf \hspace{3pt} grad \hspace{3pt}} f$.

Theorem. Suppose

$F = (P,Q)$ and $P_y = Q_x$ on region $D$.

Then $F$ is conservative provided $D$ is simply connected.

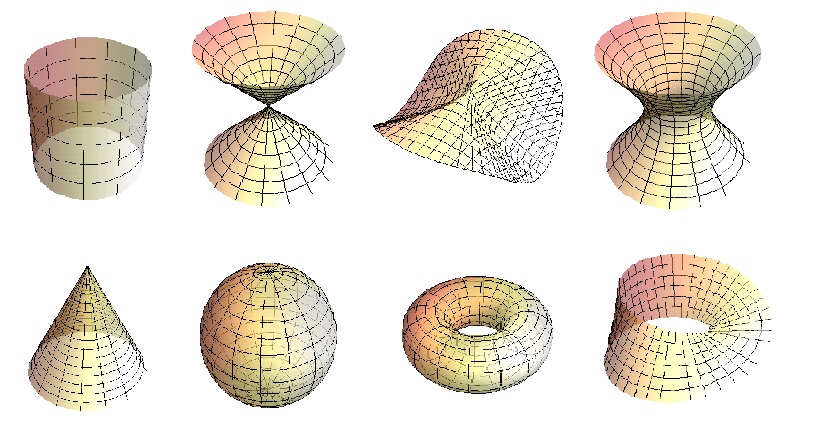
Exercise: Determine which ones of these surfaces are simply connected (sphere, torus, pretzel, cylinder, cone, plane, paraboloid, saddle, double cone).

For more see Fundamental group.

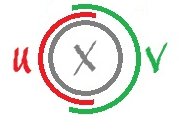
Theorem. Suppose $$X=U \cup V,$$ where

• $U,V$ are simply connected, and
• $U \cap V$ is path-connected.

Then $X$ is simply connected.

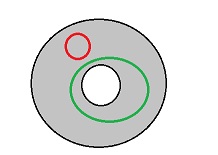
Exercise. Apply the theorem to these subsets of circle ${\bf S}^1$:

Proof. Suppose $\alpha:[0,1] \to X$ is a loop. We claim that $$\alpha \sim \beta_1\cdot...\cdot\beta_s,$$ where $\beta_1...\beta_s$ are loops too and

• $\beta_i \in <\beta_i> \in$
  • $\pi_1(U)$, or
  • $\pi_1(V),$

and, since both groups are trivial, each $\beta_i$ is homotopic to a constant.

We assume base $p\in U\cap V$.

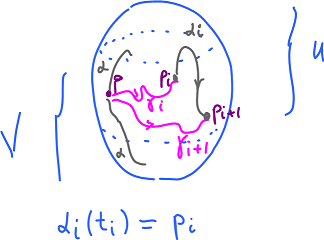
Now, $\alpha$ is a loop based in $p$: $$\alpha:[0,1] \to X,\alpha(0)=\alpha(1)=p.$$ We break $\alpha$ into pieces $\alpha_i$, small enough so that $\alpha_i$ is in $U$ or $V$ entirely. How?

We use the Lebesgue Lemma: there is $d$ so that if $t_{i+1}-t_i<d$ then

• $[t_i,t_{i+1}] \subset \alpha^{-1}(U)$ or
• $[t_i,t_{i+1}] \subset \alpha^{-1}(V)$.

Then, if we define $$\alpha_i=\alpha\bigg|_{[t_i,t_{i+1}]}$$ then its image is a subset of $U$ or subset of $V$.

We can't use $\alpha_i$'s because they aren't loops. Then we build loops...

$U\cap V$ is path connected, so there is a path $\gamma_i$ from $p=p_1$ to $p_i$.

Let's compute $$\alpha=\alpha_{1}\cdot\alpha_{2}\cdot...\alpha_{i}\cdot\alpha_{i+1}\cdot...\cdot\alpha_{s}.$$ Insert the trivial loops $[\gamma_{i}\cdot\gamma_{i}^{-1}]$: $$\alpha=\alpha_{1}\cdot[\gamma_{1}\cdot\gamma_{1}^{-1}]\cdot\alpha_{2}\cdot[\gamma_{2}\cdot\gamma_{2}^{-1}]\cdot...\cdot[\gamma_{i-1}\cdot\gamma_{i-1}^{-1}]\cdot\alpha_{i}\cdot[\gamma_{i}\cdot\gamma_{i}^{-1}]\cdot\alpha_{i+1}\cdot...\cdot[\gamma_{s-1}\cdot\gamma_{s-1}^{-1}]\cdot\alpha_{s}.$$ Rearrange: $$\alpha=[\alpha_{1}\cdot\gamma_{1]}\cdot[\gamma_{1}^{-1}\cdot\alpha_{2}\cdot\gamma_{2}]\cdot[\gamma_{2}^{-1}\cdot...\cdot\gamma_{i-1}\cdot[\gamma_{i-1}^{-1}\cdot\alpha_{i}\cdot\gamma_{i}]\cdot[\gamma_{i}^{-1}\cdot\alpha_{i+1}\cdot...\cdot\gamma_{s-1}]\cdot[\gamma_{s-1}^{-1}\cdot\alpha_{s}].$$ Now, these are loops.

This is what we know:

• $\alpha_i$ is on $U$ or $V$,
• $\gamma_i$ is in $U\cap V$.

Therefore

• $\beta_i=\gamma_i\cdot\alpha_i\cdot\gamma_{i+1}$ is in $U$ or $V$.

Then the loop $\beta_i$ represents an element of $\pi_1(U)$ or $\pi_1(V)$, both trivial!

• $\Rightarrow \beta_i\sim p$,
• $\Rightarrow \beta_1\cdot...\cdot\beta_s\sim p$.
• $\Rightarrow \alpha\sim p$.

Hence $\pi_1(X)=0$. $\blacksquare$

Example. For the sphere ${\bf S}^2$, choose $U={\bf S}^2-N$ and $V={\bf S}^2-S$, remove the north and south poles. Hence $$\pi_1({\bf S}^2)=0.$$

Exercise. Add a membrane to the sphere.

Exercise. Prove: $$\pi_1({\bf S}^n)=0.$$

Same idea but with surfaces rather than curves: every closed surface can be "contracted" to a point without leaving $X$. Or we could use spheres only here but then we would miss the void of the torus: a sphere on it has to be flat and, therefore, contractible. For more see Homotopy groups.