This site is being phased out.
Simplicial maps
Contents
The definition
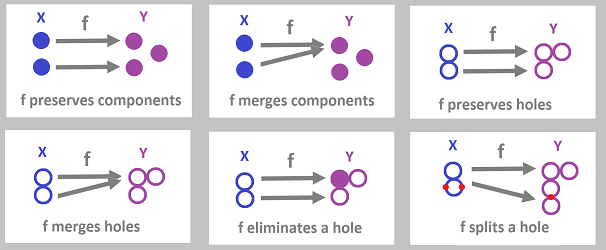
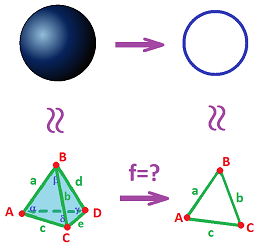
Suppose we have a map $h:X\to Y$ between two topological spaces. To fully understand this map, we want to track each of the topological features, i.e., the homology classes, in $X$ as they are transformed into the ones in $Y$:
These are the “topological events” that we previously saw happen under graph maps. In general, there will be much more happening. For example, can a void be transformed into a tunnel, or vice versa?
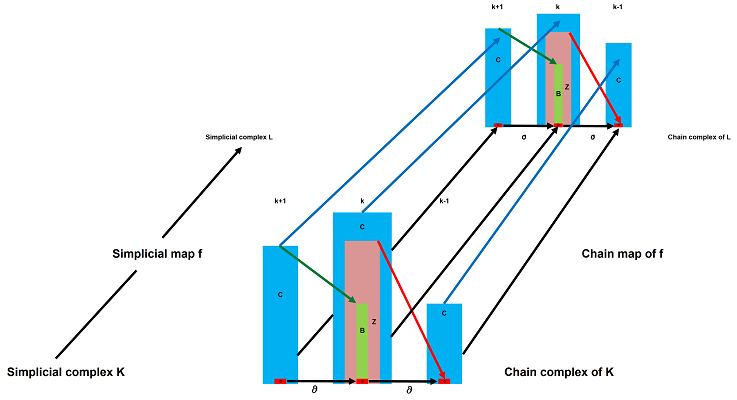
Now, suppose that $X$ and $Y$ are triangulated by two simplicial complexes: $X=|K|,Y=|L|$. We want to see map $h$ as a “realization” $h=|f|$ of a “simplicial” map $f:K\to L$ between these complexes: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccc} K &\ra{ realization } & |K| \\ \ \ \da{f} &\ra{ realization } & \ \ \da{|f|} \\ L &\ra{ realization } & |L| \end{array} $$
Let's first review graph maps.
Recall that those are simply functions of nodes of the graph that produce also functions of edges -- allowing an edge to be taken to a node, by means of a “collapse”. Since graphs are $1$-dimensional simplicial complexes, we can rewrite those definitions using the language of simplices.
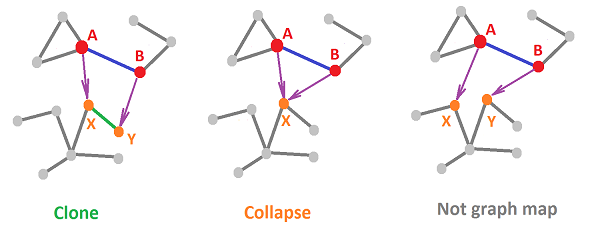
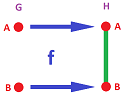
A graph map $f:K\to L$ is a function between graphs $K,L$ that satisfies, for each edge $e$, either:
- 1. (cloning) $f(e)$ is an edge $g$ and $f$ takes the end-points of $e$ to the end-points of $g$; or
- 2. (collapsing) $f(e)$ is a node $P$ and $f$ takes the end-points of $e$ to $P$.
These conditions guarantee discrete continuity:
These are the axioms written in a more compact form:
- 1. $f(AB)=f(A)f(B)$;
- 2. $f(AB)=P \Rightarrow f(A)=f(B)=P$.
The second axiom is implied by the first if we understand that an edge given by two identical nodes is a node, that node: $$PP:=P.$$
Following this idea, we introduce the following.
Notation. We allow repetition of vertices in the list that defines a simplex. A list of vertices $$s=A_0 ... A_n$$ is an $m$-simplex if there are exactly $m+1$ distinct vertices on the list.
Now, to understand what a simplicial map $f:K\to L$ between two (so far non-oriented) simplicial complexes is, we first assume that $f$ is defined on vertices only: if $A$ is a vertex in $K$ then $f(A)$ is a vertex in $L$. This function is, so far, arbitrary but not every such function can be extended to the whole complex $K$!
Let's suppose $$s=A_0 ... A_n \in K$$ and define $f(s)\in L$. We know that this simplex will have to be determined by the values of $f$ at these vertices -- the values are already known as vertices in $L$ -- as follows: $$f(s)=f(A_0 ... A_n):=f(A_0) ... f(A_n).$$ The latter is an $m$-simplex ($m \le n$), which may or may not belong to $L$. It has to, for the function defined this way to make sense.
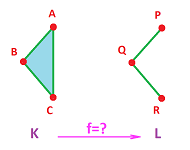
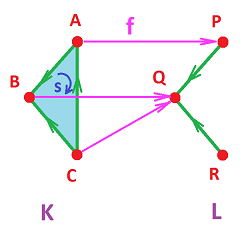
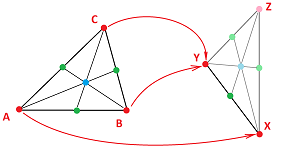
Example. Let's consider possible maps between these two complexes:
- $K=\{A, B, C, AB, BC, CA, ABC\}$,
- $L=\{P, Q, R, PQ, QR\}$.
We start with: $$f(A)=P,\ f(B)=Q,\ f(C)=R.$$ Then, by the above formula, we have $$f(AB)=PQ \in L,\ f(BC)=QR \in L,\ f(CA)=RP \not\in L.$$ Such a simplicial map is impossible!
Let's try another value for $C$: $$f(A)=P,\ f(B)=Q,\ f(C)=Q.$$ Then, two edges clone and one collapses: $$f(AB)=PQ \in L,\ f(BC)=Q \in L,\ f(CA)=PQ \in L;$$ and the triangle collapses too: $$f(ABC)=PQ \in L.$$ That works! The result is below:
$\square$
Exercise. Consider three more possibilities.
Definition. A function $f:K\to L$ between two (non-oriented) simplicial complexes is called a simplicial map if $$A_0 ... A_n \in K \Rightarrow f(A_0) ... f(A_n) \in L;$$ then, the values is defined by: $$f(A_0 ... A_n):=f(A_0) ... f(A_n).$$ A bijective simplicial map is called a simplicial isomorphism.
Theorem. A simplicial map $f:K\to L$ is a simplicial isomorphism if and only if it is bijective on vertices.
Theorem. A constant map $C:K\to L$ defined by $f(s)=V$ for some fixed vertex $V\in L$ is a simplicial map.
Theorem. The composition $gf:K\to M$ of two simplicial maps $f:K\to L$ and $g:L\to M$ is a simplicial map.
Exercise. Prove these theorems.
Exercise. Provide a simplicial map that “represents” the following map $f:{\bf S}^1\to {\bf T}^2$.
Exercise. Prove that simplicial complexes, together with simplicial maps, form a category.
Exercise. Give the graph of a simplicial map a structure of a simplicial complex.
Exercise. Define cubical maps.
As we shall see, simplicial maps are realized as continuous functions. But first we will consider the effect of these maps on the homology classes.
Chain maps of simplicial maps
Suppose a simplicial map $$f:K \to L$$ between two oriented simplicial complexes is given. The map records where every simplex goes, but what about chains? We want now to define the corresponding linear operators: $$f_k:C_k(K) \to C_k(L),\ k=0,1,....$$
Since the $k$-simplices of $K$ form a basis of the $k$-chain group $C_k(K)$, we only need to know the values of $f_k$ for these simplices. And we do, from $f$.
The only problem is that, while $s$ is a $k$-simplex in $K$, its image $f(s)$ might be a simplex in $L$ of a lower dimension. Therefore, if $s$ collapses, then $f(s) \not\in C_k(L)$, so that $f(s)$ appears to be undefined! To get out of this conundrum, we observe that $f(s)$ is undefined because it's not a $k$-simplex. What if we think of it as a $k$-chain? Then, $f(s)$ is a $k$-chain and an $m$-chain for some $m<k$, at the same time. There is, in fact, such a chain. It's $0$!
So, this is how we define the chain maps $f_0,...,f_k,...$ for $f$.
Definition. For a given $n$-simplex in $K$ $$s = A_0A_1 ... A_n,$$ where $A_0, A_1, ..., A_n$ are its vertices, we have $$f_n(s):=\begin{cases} f(A_0) ... f(A_n), & \text{ if } f(A_i) \neq f(A_j), \forall i≠j; \\ 0, & \text{ otherwise.} \end{cases}$$
Thus, a simplex is cloned or it is taken to $0$.
Example. Let's consider these two complexes from last subsection but first orient them, arbitrarily:
- $K=\{A, B, C, AB, CB, CA, ACB\}$,
- $L=\{P, Q, R, PQ, RQ\}$.
This is the simplicial map we considered above: $$f(A)=P,\ f(B)=Q,\ f(C)=Q.$$
These three identities immediately give us the three columns of the matrix of the linear operator $f_0:C_0(K)\to C_0(L)$, or $f_0:{\bf R}^3\to {\bf R}^3$: $$f_0=\left[ \begin{array}{cccccccccc} 1 &0 &0 \\ 0 &1 &1 \\ 0 &0 &0 \end{array} \right].$$
Further, the simplicial identities $$f(AB)=PQ,\ f(BC)=Q,\ f(CA)=PQ,$$ give us these chain identities: $$f_1(AB)=PQ,\ f_1(BC)=0,\ f_1(CA)=QP.$$ These three give us the three columns of the matrix of the linear map $f_1:C_1(K)\to C_1(L)$, or $f_1:{\bf R}^3\to {\bf R}^2$: $$f_1=\left[ \begin{array}{cccccccccc} 1 &0 &-1 \\ 0 &0 &0 \end{array} \right].$$
Finally, the simplicial identity $$f(ABC)=PQ$$ gives us the chain identity: $$f_2(ACB)=0.$$ Therefore, $$f_2=0.$$ $\square$
Exercise. Add a $2$-simplex to either of these two simplicial complexes, orient the new complexes, and then find the matrices of the chain maps of these two simplicial maps:
The definition of $f_n$ is simple enough, but we can make it even more compact if we observe that
- case 1: $f_n(s)=f(A_0) ... f(A_n)$, if $f(A_i) \neq f(A_j)$, for all $i\ne j$;
implies
- case 2: $f_n(s)=0$, if $f(A_i) = f(A_j)$, for some $i\ne j$.
The reason is that having two coinciding vertices in a simplex -- understood as a chain -- make it equal $0$. Indeed, when we flip them, the sign has to flip too; but it's the same simplex! $$\begin{array}{lll} B_i=B_j \Rightarrow\\ B_0 ... B_i ... B_j ... B_n &= -B_0 ... B_j ... B_i ... B_n \\ &=-B_0 ... B_i ... B_j ... B_n. \end{array}$$ It must be zero then.
Then we amend the convention from the last subsection.
Notation. We allow repetition of vertices in the list that defines a simplex. However, a list of vertices $$s=A_0 ... A_n$$ defines a $0$-chain unless there are exactly $n+1$ distinct vertices on the list.
Definition. The $n$-chain map $f_n:C_n(K) \to C_n(L)$ induced by a simplicial map $f:K \to L$ is defined by its values on the simplices, as follows: $$f_n(A_0 ... A_n):=f(A_0) ... f(A_n).$$
Theorem. The chain map induced by a simplicial isomorphism is an isomorphism. Moreover, the chain map induced by the identity simplicial map is the identity.
Theorem. The chain map induced by a simplicial constant map $C:K\to L$ with $K,L$ edge-connected is acyclic: $C_0=\operatorname{Id},\ C_k=0,\ \forall k>0$.
Theorem. The chain map induced by the composition $gf:K\to M$ of two simplicial maps $f:K\to L$ and $g:L\to M$ is the composition of the chain maps induced by these simplicial maps: $$(gf)_k=g_kf_k.$$
Exercise. Prove these theorems.
Since we have two simplicial complexes, there are two chain complexes: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} ...& \to & C_{k+1}(K)& \ra{\partial_{k+1}} & C_{k}(K)& \ra{\partial_{k}} & C_{k-1}(K)& \to&...& \to & 0,\\ ...& \to & C_{k+1}(L)& \ra{\partial_{k+1}} & C_{k}(L)& \ra{\partial_{k}} & C_{k-1}(L)& \to&...& \to & 0. \end{array} $$ The chain maps connect these two chain complexes item by item, “vertically”, like this: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccc} ...& \to & C_{k+1}(K)& \ra{\partial_{k+1}} & C_{k}(K)& \ra{\partial_{k}} & C_{k-1}(K)& \to&...& \to & 0\\ ...& & \da{f_{k+1}}& & \da{f_{k}}& & \da{f_{k-1}}& &...& & \\ ...& \to & C_{k+1}(L)& \ra{\partial_{k+1}} & C_{k}(L)& \ra{\partial_{k}} & C_{k-1}(L)& \to&...& \to & 0. \end{array} $$ The arrows here are maps and paths of arrows are their compositions. The question is then, are the results “path-independent”? In other words, is the diagram commutative?
Exercise. Produce such a diagram for the map in the example above.
Exercise. Define chain maps between chain complexes in such a way that together they form a category.
Chain maps and the boundary operators
We need to understand how a chain map interacts with the boundary operator.
There are two boundary operators to deal with for a given simplicial map $$f:K\to L,$$ for either of the complexes: $$\partial ^K_k: C_k(K) \to C_{k-1}(K)$$ and $$\partial ^L_k: C_k(L) \to C_{k-1}(L).$$ (Both the subscripts and the superscripts may be omitted.) Along with the chain maps of $f$, the boundary operators can be put in one diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccc} C_k(K) & \ra{f_k} & C_k(L) \\ \da{\partial ^K_k} & \searrow & \da{\partial ^L_k} \\ C_{k-1}(K) & \ra{f_{k-1}} & C_{k-1}(L). \end{array} $$ As we shall see, the diagram commutes. The familiar and wonderfully compact form of this condition is $$\begin{array}{|c|} \hline \quad \partial f=f \partial \quad \\ \hline \end{array} $$
This behavior is expected. After all, when a simplex is cloned, so is its boundary, face by face:
It is the case of collapse that needs special attention. We will prove the general case.
For the proof we will need the following. Both boundary operators are defined by the same formula for $k=0,1,...$: $$\partial_k( A_0 ... A_k ) := \displaystyle\sum_{i=0}^k(-1)^i A_0 ... [A_i] ... A_k. \text{ (1)}$$ We will also need the definition of the chain map of a simplicial map: $$f_{k} (A_0 ... A_k):= f(A_0) ... f(A_i) ... f(A_k). \text{ (2)}$$
Theorem (Algebraic Continuity). If $f:K\to L$ is a simplicial map, then its chain maps satisfy for $k=1,2,...$: $$\partial^L_k f_k = f_{k-1} \partial^K_k.$$
Proof. By examination. To prove the identity, we evaluate its left-hand side and its right-hand side for $$s = A_0A_1 ... A_k \in C_k(K).$$
First, the right-hand side. We use (1), $$\begin{array}{lll} f_{k-1}( \partial_k(s)) &= f_{k-1} \left( \displaystyle\sum_{i=0}^k (-1)^i A_0 ... [A_i] ... A_k \right), &\text{ then by linearity} \\ &= \displaystyle\sum_{i=0}^k (-1)^i f_{k-1} (A_0 ... [A_i] ... A_k), &\text{ then by (2)} \\ &= \displaystyle\sum_{i=0}^k (-1)^i f(A_0) ... [f(A_i)] ... f(A_k). \end{array}$$
Next, the left-hand side. We use (2), $$\begin{array}{lll} \partial_k(f_k(s)) &= \partial_k(f(A_0) ... f(A_k)), &\text{ then by (1) } \\ &= \displaystyle\sum_{i=0}^k (-1)^i f(A_0) ... [f(A_i)] ... f(A_k). \end{array}$$
Now, as we have proven the identity for all basis elements, simplices of the vector space, $C_k(K)$, then the two linear operator coincide.
$\blacksquare$
Corollary. The theorem holds for chains over ${\bf Z}_2$.
Exercise. Prove the corollary (a) by re-writing the above proof, (b) directly from the theorem. Hint: consider a function ${\bf Z}\to {\bf Z}_2$.
Homology maps
Thus, a simplicial map induces chain maps between the two chain complexes, but what about the homology? What is the effect of the map on the homology classes?
Algebraically, this is what we are after. We already have a linear operator $$f_k : C_k(K) \to C_k(L)$$ with the above property. And now we need to define somehow another linear operator, the quotient operator, $$?: H_k(K) = \frac{Z_k(K)}{ B_k(K)} \to H_k(L) = \frac{ Z_k(L)}{ B_k(L)},$$ where $$Z_k(K):=\ker \partial ^K_k , B_k(K):=\operatorname{Im} \partial ^K_{k+1},$$ $$Z_k(L):=\ker \partial ^L_k , B_k(L):=\operatorname{Im} \partial ^L_{k+1},$$ are the groups of cycles and the groups of boundaries of these complexes.
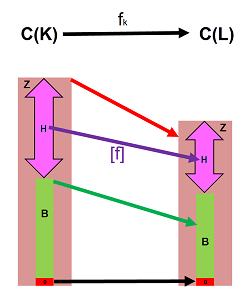
The way the new maps have connected the two chain complexes is informally illustrated by this diagram:
We need to see the interaction between these subspaces. We already know that our quotient operator is well defined provided these conditions are satisfied:
- (1) $f_k(Z_k(K)) \subset Z_k(L),$
- (2) $f_k(B_k(K)) \subset B_k(L).$
We will prove these two facts by using the algebraic continuity condition: $\partial f = f \partial$. Then, both squares of this diagram are commutative: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccc} C_{k+1}(K)& \ra{\partial_{k+1}} & C_{k}(K)& \ra{\partial_{k}} & C_{k-1}(K)\\ \da{f_{k+1}}& & \da{f_{k}}& & \da{f_{k-1}}\\ C_{k+1}(L)& \ra{\partial_{k+1}} & C_{k}(L)& \ra{\partial_{k}} & C_{k-1}(L). \end{array} $$
The proofs below are standard in algebraic topology.
Corollary. Chain maps take cycles to cycles: $$f_k(Z_k(K) ) \subset Z_k(L).$$
Proof. Suppose $x \in Z_k(K)$, then $\partial_k(x) = 0$. Then, we trace $x$ in the right square of the diagram: $$\begin{array}{ll} \partial_k f_k(x) &= f_{k-1} \partial_k (x) \\ &= f_{k-1}(0) \\ &= 0. \end{array}$$ Hence $f_k(x)$ is a cycle too. $\blacksquare$
Corollary. Chain maps take boundaries to boundaries: $$f_k( B_k(K) ) \subset B_k(L).$$
Proof. Suppose $x \in B_k(K),$ then $x = \partial_{k+1}(u)$ for some $u \in C_{k+1}(K)$. Then, we trace $x$ back in the left square of the diagram: $$\begin{array}{llll} f_k(x) &= f_k \partial_{k+1}(u) \\ &= \partial_{k+1}f_{k+1}(u). \end{array}$$ Hence $f_k(x)$ is a boundary too. $\blacksquare$
The two results are summarized below:
Thus, we are able to restrict $f_k$ to cycles: $$f_k : Z_k(K) \to Z_k(L),$$ or to boundaries: $$f_k : B_k(K) \to B_k(L).$$
Therefore, the definition below is legitimate.
Definition. Given chain maps $$f_k : C_k(K) \to C_k(L),\ k=0,1,2...$$ (possibly induced by a simplicial map $f:K \to L$), the homology maps induced by $\{f_k\}$, $$[f_k]: H_k(K) \to H_k(L), \ k=0,1,2,...,$$ are the linear operators given by $$[f_k]([x]) := [f_k(x)].$$
Notation. The brackets are often omitted: $$f_k: H_k(K) \to H_k(L),$$ or an alternative, common notation is used: $$f_*: H_k(K) \to H_k(L).$$
Exercise. Devise a simplicial map the realization of which wraps a circle around another circle $n$ times. Compute its homology.
Computing homology maps
Even with the most trivial examples we should pretend that we don't know the answer...
Example (segment). We start with these simplicial complexes (graphs) : $$G=\{A,B\},\ H=\{A,B,AB\},$$ and $$f(A)=A,\ f(B)=B.$$
This is the inclusion:
Then, on the chain level we have: $$\begin{array}{llllll} C_0(G)=< A,B >,& C_0(H)= < A,B >,\\ f_0(A)=A,& f_0(B)=B & \Rightarrow f_0=\operatorname{Id};\\ C_1(G)=0,& C_1(H)= < AB >\\ &&\Rightarrow f_1=0. \end{array} $$ Meanwhile, $\partial _0=0$ for $G$ and for $H$ we have: $$\partial _1=[-1, 1]^T.$$ Therefore, on the homology level we have: $$\begin{array}{lllll} H_0(H):= \frac{ Z_0(H) }{ B_0(H) }&=\frac{C_0(H) }{ \partial _1(<AB>) } = \frac{< A,B >}{< B-A > }&=< [A+B] >,\\ H_0(H):= \frac{ Z_0(H) }{ B_0(H) }&=\frac{C_0(H) }{ \partial _1(<AB>) } = \frac{< A,B >}{< B-A > }&=< [A+B] >,\\ H_1(G):= \frac{ Z_1(G) }{ B_1(G) }&= \frac{0 }{ 0 }&=0,\\ H_1(H):= \frac{ Z_1(H) }{ B_1(H) }&= \frac{0 }{ 0 }&=0. \end{array} $$ Then, by definition,
- $[f_0]([A]):=[f_0(A)]=[A],[f_0]([B])=[f_0(B)]=[B] \Rightarrow f_0=[1,1]^T;$
- $[f_1]=0.$
$\square$
Exercise. Modify the computation for the case when there is no $AB$.
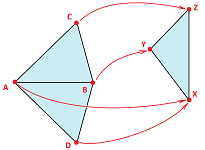
Example (two segments). Given these two two-edge simplicial complexes:
- 1.$K=\{A,B,C,AB,BC\}$,
- 2.$L=\{X,Y,Z,XY,YZ\}$.
Consider these simplicial maps:
- 1. $f(A)=X,\ f(B)=Y,\ f(C)=Z,\ f(AB)=XY,\ f(BC)=YZ$;
- 2. $f(A)=X,\ f(B)=Y,\ f(C)=Y,\ f(AB)=XY,\ f(BC)=Y$,
They are given below:
We think of these identities as functions evaluated on the generators of the two chain groups:
- 1. $C_0(G)=< A,B,C >,\ C_1(G)=< AB,BC >$;
- 2. $C_0(H)=< X,Y,Z >,\ C_1(H)=< XY,YZ >$.
These functions induce these two linear operators: $$f_0:C_0(G) \to C_0(H),\ f_1:C_1(G) \to C_1(H),$$ as follows.
The first function gives these values:
- $f_0(A)=X,\ f_0(B)=Y,\ f_0(C)=Z,$
- $f_1(AB)=XY,\ f_1(BC)=YZ$.
Those, written coordinate-wise, produce the columns of its matrices: $$f_0=\left[\begin{array}{ccccc} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array} \right] =\operatorname{Id}; f_0=\left[\begin{array}{ccccc} 1&0\\ 0&1 \end{array} \right] =\operatorname{Id}.$$ The second produces:
- $f_0(A)=X,\ f_0(B)=Y,\ f_0(C)=Y,$
- $f_1(AB)=XY,\ f_1(BC)=0$,
which leads to: $$f_0=\left[\begin{array}{ccccc} 1&0&0\\ 0&1&1\\ 0&0&0 \end{array} \right]; f_0=\left[\begin{array}{ccccc} 1&0\\ 0&0 \end{array} \right].$$
The first linear operator is the identity and the second can be thought of as a projection.
$\square$
Exercise. Modify the computation for the case of an increasing and then decreasing function.
Now homology...
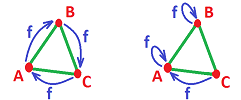
Example (hollow triangle). Suppose: $$G=H:=\{A,B,C,AB,BC,CA\},$$ and $$f(A)=B,\ f(B)=C,\ f(C)=A.$$
This is a rotated triangle:
The homology maps are computed as follows: $$Z_1(G)=Z_1(H)=< AB+BC+CA >.$$ Now, $$f_1(AB+BC+CA)=f_1(AB)+f_1(BC)+f_1(CA)=BC+CA+AB=AB+BC+CA.$$ Therefore, $f_1:Z_1(G)\to Z_1(H)$ is the identity and so is the homology map $[f_1]:H_1(G)\to H_1(H)$. Conclusion: the hole is preserved.
Alternatively, we collapse the triangle onto one of its edges: $$f(A)=A,\ f(B)=B,\ f(C)=A.$$ Then $$f_1(AB+BC+CA)=f_1(AB)+f_1(BC)+f_1(CA)=AB+BA+0=0.$$ So, the map is zero. Conclusion: collapsing of an edge causes the hole collapse too.
$\square$
Exercise. Modify the computation for the case (a) a reflection and (b) a collapse to a vertex.
How to classify simplicial maps
From the fact that vertices are taken to vertices we derive this simple conclusion.
Proposition. If complexes $K,L$ are edge-connected, any simplicial map between them induces the identity on the $0$th homology group: $$[f_0]=\operatorname{Id}:H_0(K)={\bf R} \to H_0(L)={\bf R}.$$
Therefore, not every linear operator between the homology groups can be “realized” as the homology map of a simplicial map.
Exercise. Suppose $K$ has $n$ edge-components and $L$ has $m$. List all possible $0$th homology maps between them.
What follows is a typical homological argument.
Example. With our knowledge of the homology groups of the circle ${\bf S}^1$ and of the sphere ${\bf S}^2$: $$H_0({\bf S}^1)={\bf R},\ H_1({\bf S}^1)={\bf R},\ H_2({\bf S}^1)=0;$$ $$H_0({\bf S}^2)={\bf R},\ H_1({\bf S}^2)=0,\ H_2({\bf S}^2)={\bf R};$$ we can now answer the question whether it's possible to transform voids into tunnels:
It is not! The answer is understood in the sense that there is no map $$f:{\bf S}^2 \to {\bf S}^1$$ that preserves the homology class of the void of the sphere. The reason is simple, the homomorphism $$[f_1]:H_1({\bf S}^2)=0 \to H_1({\bf S}^1)={\bf R}$$ can only be trivial. In particular, if $s$ is the $1$-homology class representing the void in the sphere, then $[f_1](s)=0$. The void must collapse!
The answer applies to any other choice of triangulations of the two spaces.
$\square$
Exercise. What happens to the hole of the circle if it is mapped to the sphere?
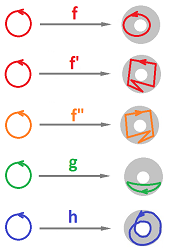
Exercise. (a) Interpret these maps as maps of ${\bf S}^1$ to ${\bf S}^1$:
and represent those as realizations of simplicial maps. Hint: the last one will need special attention. (b) Confirm by computation that their homology maps are: $$[f]=\operatorname{Id},\ [f']=-\operatorname{Id},\ [g]=0,\ [h]=2\cdot \operatorname{Id}.$$ (c) Make sense of this alternative answer: $$[f]=-\operatorname{Id},\ [f']=\operatorname{Id},\ [g]=0,\ [h]=-2\cdot \operatorname{Id}.$$
Theorem. The homology map induced by an isomorphic chain map (and, moreover, by a simplicial isomorphism) is an isomorphism. The homology map induced by the identity chain map (and, moreover, by the identity simplicial map) is the identity operator.
Theorem. The homology map induced by an acyclic chain map, $f_k=0,\ k=1,2...$, (and, moreover, by a constant simplicial map) is trivial, i.e., the zero operator.
Theorem. The homology map induced by the composition
- $g_kf_k:C_k(K)\to C_k(M),\ k=0,1,...,$
of chain maps
- $f_k:C_k(K) \to C_k(L),\ k=0,1,...,$ and
- $g_k:C_k(L) \to C_k(M),\ k=0,1,...,$
(and, moreover, by the composition of simplicial maps $f,g$) is the composition of the homology maps induced by these chain maps: $$[g_kf_k]=[g_k][f_k],$$ and, moreover: $$[(gf)_k]=[g_k][f_k].$$
Exercise. Prove these theorems.
Realizations
We already know that an abstract simplicial complex $K$ can be realized as a topological space. The way to construct it is by treating the list of vertices and simplices of $K$ as a blueprint of a geometric complex $|K| \subset {\bf R}^N$. It is built from the geometric $n$-simplices (corresponding to the simplices of $K$), i.e., the convex hulls of $n+1$ points $$A_0A_1 ... A_n = \operatorname{conv}\{A_0, A_1, ..., A_n\}$$ in general position. In the simplex, every point $x$ is represented as a convex combination of the vertices: $$x = \displaystyle\sum_i s_i A_i,$$ with the barycentric coordinates of $x$ serving as coefficients.
Now we want to learn how to realize simplicial maps -- as continuous functions!
Of course, we want $f:K\to L$ to be realized as $|f|:|K|\to |L|$.
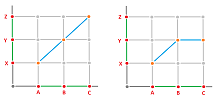
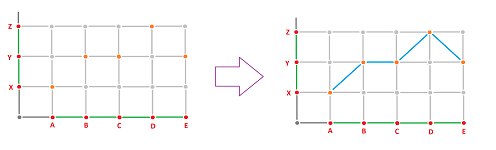
The $1$-dimensional case is the case of graphs. Let's review what we know about maps of graphs. Suppose two complexes are realized in ${\bf R}$ and suppose we are provided with only the values of the vertices of the simplicial map:
- $f(A)=X,\ f(B)=Y,\ f(C)=Y,\ f(D)=Z,\ f(E)=Y$.
Then, of course, we have
- $|f|(A)=X,\ |f|(B)=Y,\ |f|(C)=Y,\ |f|(D)=Z,\ |f|(E)=Y$.
These points are plotted in orange below:
We reconstruct the rest of the map by connecting these points by straight segments. The formulas are familiar, for example: $$|f|(tA+(1-t)B)=tX+(1-t)Y,\ t\in [0,1].$$ The idea becomes clear: we use the barycentric coordinates of each point in a simplex as the barycentric coordinates of the image of that point.
It is similar in dimension $2$:
In particular, we can see: $$|f|\left(\frac{1}{2}A+\frac{1}{2}B\right)=\frac{1}{2}X+\frac{1}{2}Y,$$ $$|f|\left(\frac{1}{3}A+\frac{1}{3}B+\frac{1}{3}C\right)=\frac{1}{3}X+\frac{1}{3}Y+\frac{1}{3}Z.$$
This approach to realizing simplicial maps by linearity doesn't work for cubical complexes. The reason is that, for example, a square has $4$ vertices and, therefore, they can't be in general position. That's why the analog of the barycentric coordinates (with respect to the vertices) doesn't provide a unique representation of a point in the square.
Collapses are realized the same way -- linearly -- for simplicial complexes:
In particular, consider: $$|f|\left(\frac{1}{3}A+\frac{1}{3}B+\frac{1}{3}C\right)=\frac{1}{3}X+\frac{1}{3}Y+\frac{1}{3}Y = \frac{1}{3}X+\frac{2}{3}Y.$$
Exercise. Plot the images of the green points and the blue point.
This approach won't work for cubical complexes. As an example, a function $g:[0,1]\times [0,1] \to [0,1]$ with $$g(0,0)=g(1,1)=0,\ g(1,0)=g(0,1)=1,$$ can't be linear.
Exercise. Prove it.
Now the general case.
We start with a single simplex. Given a simplicial map between two (abstract) simplices $$f: \sigma \to \tau ,$$ here's how we define a map that will serve as its realization $$|f|: |\sigma |\to |\tau |.$$ Suppose the dimensions are $n$ and $m \le n$ respectively and $$\sigma = A_0 ... A_n, \ \tau = B_0 ... B_m.$$ Suppose $A_0, ..., A_n$ and $B_0, ..., B_m$ also denote the vertices in the realizations of these simplices $|\sigma |$ and $|\tau |$. Now suppose a point $x\in |\sigma |$ is given by its barycentric coordinates: $$x = \displaystyle\sum_i s_i A_i.$$ The coefficients are unique. We can assume that the values $$|f|(A_i)=B_{j_i},\ i=0,....,n,$$ are already set as vertices in $|\tau |$. Then we define $$|f|(x) = \displaystyle\sum_i s_i |f|(A_i).$$
Some of the terms $|f|(A_i)$ in the right-hand side may be equal. Therefore, we don't claim that, unless $\sigma$ is cloned, $s_i$ are the barycentric coordinates of $|f|(x)$ in $|\tau|$, but rather in a face of $|\tau|$.
Exercise. Prove that $|f|(x) \in |\tau |$.
The new map is linear on each simplex as $$|f|(x) = |f| \left( \displaystyle\sum_i s_i A_i \right) = \displaystyle\sum_i s_i |f|(A_i).$$ More precisely, $|f|$ should be called convex rather than linear. The new map is piecewise linear.
Given complexes $K$ and $L$ and a simplicial map $f:K\to L$, we have a map $$g=|f|:|K|\to |L|$$ constructed one simplex at a time, as described above. It is called a realization of simplicial map $f$.
Exercise. Describe how this map can be constructed skeleton by skeleton.
Theorem. A realization of a simplicial map is well-defined and continuous.
Exercise. Prove the theorem. Hint: show that if two simplices share a face, the formulas for the function restricted to this face match.
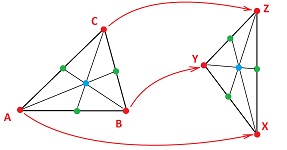
In the first example above, the $2$-simplex is cloned and in the second, it is collapsed. The data structure of abstract simplicial complexes and maps and the geometry of their realizations match, as follows:
Proposition. Under a simplicial map $f:K\to L$, a simplex $s\in K$ is cloned if and only if its realization $|s|$ is mapped homeomorphically under a realization $|f|$ of $f$.
A function $g: |K| \to |L|$ of the (geometric) realizations two simplicial complexes $K$ and $L$ is called a geometric simplicial map if
- $g$ maps every vertex to a vertex, and
- $g$ is linear on each (geometric) simplex.
The topological issues, as opposed to the geometrical issues, of the realizations of simplicial maps will be discussed later under cell maps.
Social choice: no compromise
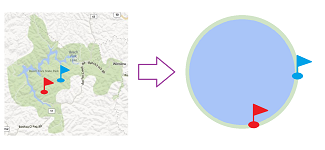
Let's recall the problem of social choice for two hikers.
We need to develop a procedure for finding a fair compromise on the location of the camp on the shore of a lake:
Social choice problem: is there a map $$f:{\bf S}^1\times{\bf S}^1\to {\bf S}^1$$ that satisfies these two conditions:
- 1. $f(x,y)=f(y,x)$, and
- 2. $f(x,x)=x?$
We already know that some obvious solutions fail.
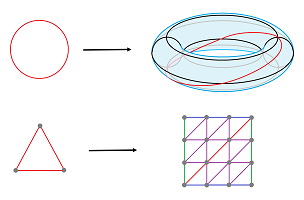
To recognize the geometry, note that ${\bf S}^1\times{\bf S}^1$ is simply the torus:
For now, we will limit ourselves to the simplicial case:
- the circle is triangulated;
- the torus is triangulated;
- its diagonal $\Delta$ of the torus is triangulated identically to the circle;
- the diagonal map $\delta: {\bf S}^1 \to \Delta$ given by $\delta (x)=(x,x)$ is the identity simplicial map;
- the choice function is a simplicial map.
Let's translate this problem into the homological language.
We know that $f$, if it exists, induces a homomorphism $$[f_1]:H_1({\bf S}^1)\to H_1({\bf S}^1)$$ on the homology groups: $$H_1({\bf S}^1)={\bf Z},\ H_1({\bf S}^1 \times {\bf S}^1)={\bf Z} \oplus {\bf Z}.$$ The problem then becomes: is there a homomorphism $$g:{\bf Z}\oplus {\bf Z}\to {\bf Z},$$ whether it comes from some simplicial map $f$ or not, that satisfies
- 1. $g(x,y)=g(y,x)$, and
- 2. $g(x,x)=x?$
Exercise. Show that these two conditions indeed follow from the two conditions above.
Exercise. Restate and solve the problem for the case of real coefficients.
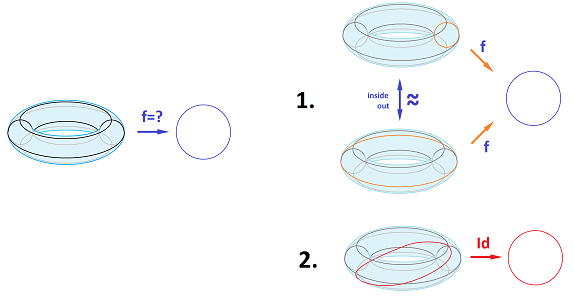
Now the problem becomes, is it possible to complete this commutative diagram of simplicial complexes and simplicial maps, with some $f$? $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccc} & {\bf S}^1 & \ra{\delta} & {\bf S}^1 \times {\bf S}^1 \\ & _{\operatorname{Id}} & \searrow & \ \ \da{f=?} \\ & & & {\bf S}^1. \end{array}$$ The diagonal arrow is the identity according to the second condition.
Applying homology to the above diagram creates a commutative diagram of groups and homomorphisms: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccc} & {\bf Z} & \ra{\delta _*=[1,1]^T} & {\bf Z} \oplus {\bf Z} \\ & _{\operatorname{Id}} & \searrow & \ \ \da{g=?} \\ & & & {\bf Z}. \end{array} $$ The problem becomes, is it possible to complete this diagram, with some $g$?
Now we use the fact that $g$ has to be symmetric. Let's choose a specific generator of the $1$-homology group: $$H_1({\bf S}^1)={\bf Z}=< 1 >$$ and identify its value under $g$: $$c:=g(1,0)\in H_1({\bf S}^1)={\bf Z}.$$ Then $$1=\operatorname{Id}(1)=g[\delta_1](1)=g(1,1)=g(1,0)+g(0,1)=2g(1,0)=2c.$$ A contradiction!
We have proven that there is no fair compromise for our social choice problem.
Exercise. Compare the outcome to that for homology over ${\bf R}$. What about ${\bf Z}_2$?
The mathematical version of the problem and the two conditions are illustrated below:
Exercise. State and solve homologically the problem of $m$ hikers and the forest of $n$ convex path-components.
Exercise. What if the two hikers are also to choose the time of the day to leave? Describe and analyze the new set of possible choices. What if they are also to choose the way to hang their hammock in the camp?
Exercise. Suppose another pair of hikers has stopped in the middle of the forest and has to decide which way to go. Discuss.
It is a common sense observation that excluding some options might make compromise impossible. Furthermore, a compromise-producing rule might also become impossible. We will see broader results later.
The fact that the analysis is limited to simplicial maps seems very unfortunate. Of course, we should be able to freely choose the values for $f$ from the continuum of locations on the shore of the lake! Later, we will extend the homology theory to arbitrary spaces and maps.