This site is being phased out.
Simplex
Geometrically, simplices are:
- point,
- closed segment,
- closed triangle,
- closed pyramid, etc.
These are, respectively,
- $0$-dimensional simplex,
- $1$-dimensional simplex,
- $2$-dimensional simplex,
- $3$-dimensional simplex, etc.
The simplest example of $n$-simplex is the polygon in ${\bf R}^n$ with $n+1$ vertices at $(0,0,0,0,...,0), (1,0,0,0,...,0), (0,1,0,0,...,0), ..., (0,0,0,0,...0,1,0), (0,0,0,0,...,0,1)$.
A geometric $n$-simplex in ${\bf R}^{n+1}$ is defined as the convex hull (the set of all convex combinations) of $n+1$ points
in general position:
If we treat the simplex as a cell complex, its topology is very simple:
Theorem. The $n$-simplex is homeomorphic to the $n$-ball ${\bf B}^n$.
There is however an additional geometric structure; a simplex has faces.
Example. Suppose $a$ is a $1$-simplex
Then its faces are $v_0$ and $v_1$. They can be easily described algebraically. An arbitrary point in a is a convex combination of $v_0$ and $v_1$:
What about $v_0$ and $v_1$? They are convex combinations too but of a special kind:
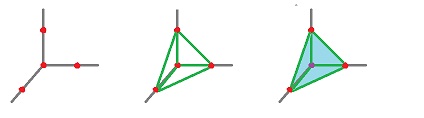
Example. Suppose ${\tau}$ is a $2$-simplex
$$a = {\rm \hspace{3pt}conv}\{v_0,v_1,v_2 \}.$$
An arbitrary point in a is a convex combination of $v_0,v_1,v_2$:
$$a_0v_0 + a_1v_1 + a_2v_2 with a_0 + a_1 + a_2 = 1.$$
To find all $1$-faces set one of these coefficient equal to $0$:
$b = a_0v_0 + a_1v_1 + a_2v_2$ with $a_0 + a_1 + a_2 = 1$ and $a_1 = 0,$
$c = a_0v_0 + a_1v_1 + a_2v_2$ with $a_0 + a_1 + a_2 = 1$ and $a_0 = 0$.So,
$$a,b,c < {\tau}.$$
To find all $0$-faces set two of these coefficient equal to $0$:
$$v_0 = 1 \cdot v_0 + 0 \cdot v_1 + 0 \cdot v_2, {\rm \hspace{3pt} etc}.$$
An abstract $n$-simplex is simply any finite set $A_0A_1...A_n$.
Exercise. Prove that the boundary of an $n$-simplex is homeomorphic to ${\bf S}^{n-1}$. Hint: put the sphere inside the simplex.
See also Simplicial complex.
Instead of ${\bf R}^n$, one can carry out this construction in any vector space.