This site is being phased out.
Saliency
Consider objects in gray scale images. The area/size of an object can be understood as its mass as if this is a lamina with uniform density. However, this approach ignores the gray values of the pixels.
In case of a gray scale image we have an alternative. We can treat the gray values as values of the density of the lamina.
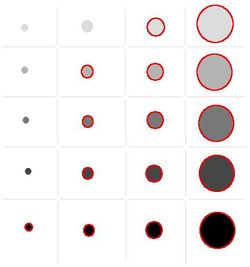
The total amount of gray, or mass (that may be a better name for this), in the object in comparison to the the surrounding area is the most complete characteristic of its importance. We will call it saliency.
Saliency of a dark object
= the sum of
(the gray value of the surrounding area - the gray value of the pixel),
over all pixels in it
Saliency of a light object
= the sum of
(the gray value of the pixel - the gray value of the surrounding area),
over all pixels in it
For example, object #11 has 280 pixels of gray level 0 (from the black rectangle #13), 567 pixels of gray level of 128 (from rectangle #12), and 4984 - 280 - 567 = 4137 pixels of gray level 192 (the rest). Since it is surrounded by white (255), its saliency is
280*(255-0) + 567*(255-128) + 4137*(255-192) = 404,040
Even though this may be the best way to approach the size and importance of objects, the algorithm is implemented in such a way that holes aren't subtracted. Just like with the area the result is that a thin curve that encloses a region is as large (important) as the region itself. Once again you can argue either way but the current approach is more feasible computationally.
The following is a more compact formula:
Saliency = the sum of | the gray value of the surrounding area - the gray value of the pixel |, over all pixels in the object
Suppose the curve on the left is the gray scale function of the image. Then the tip marked with a horizontal line corresponds to an object. Finally, the volume marked in red is the saliency of the object.
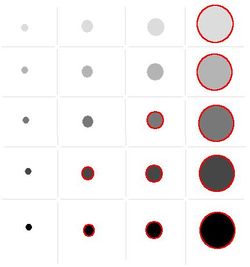
The images below show how the number of captured objects declines as the saliency threshold increases: 22,356; 52,861; 115,482. Also, observe that some larger circles have lower saliency than some smaller ones.
Exercise. Try the same with this image.
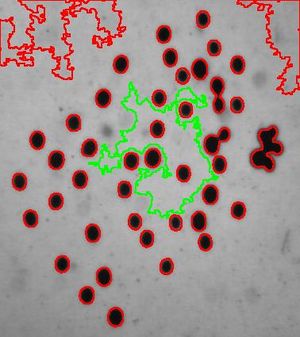
Below a segmentation is found with limitations on saliency alone. The result is better than if you use Area alone but some noise is still counted as objects - at this or other settings for the saliency. For this kind of images use Contrast or Roundness for better results.
Keep in mind that the way we define objects in images, the holes aren't subtracted!
Currently, saliency does not appear in Pixcavator's output table. You can get this number by multiplying the area by the average intensity. If you save the table as a spreadsheet, you can simply add an extra column to the table and compute saliency for each row. For other measurements, see Measuring objects.
To experiment with the concepts, download the free Pixcavator Student Edition.