This site is being phased out.
Differentiation without limits: part 2
What about derivatives of products?
Remember!
$$(f\cdot g) \neq f^{\prime}\cdot g^{\prime}$$
This is the so called "Naive Product Rule":
Verify:
$$\begin{aligned}
(x\cdot x)^{\prime} &= x^{\prime}\cdot x^{\prime} = 1\cdot 1 = 1 \\
(x^{2})^{\prime} &= 2x
\end{aligned} $$
Wrong, no match. In fact it cannot be true. Look at the units. Suppose this is about motion:
If $$ x, \text{ sec } \quad f(x), \text{ feet } \quad y = f(x)$$ and $$ x, \text{ sec } \quad g(x), \text{feet} $$ Then $$ f^{\prime}(x), \frac{\text{feet}}{\text{sec}}$$ Why $\frac{\text{feet}}{\text{second}}$? Here's why: $$ \frac{f(x + h) - f(x) \text{ feet}}{h \text{ sec}} $$ and $$ f(x)g(x), \text{ feet}^{2} $$ So $$ (f(x)g(x))^{\prime}, \frac{\text{feet}^{2}}{\text{sec}} \neq \frac{\text{feet}^{2}}{\text{sec}^{2}}$$ Therefore $$ f^{\prime}g^{\prime}, \frac{\text{feet}^{2}}{\text{sec}^{2}}$$
So, $f^{\prime}g^{\prime}$ is measured in $\frac{\text{ft}^{2}}{\text{sec}^{2}}$ and $(fg)^{\prime}$ is measured in $\frac{\text{ft}^{2}}{\text{sec}}$.
To give an example where this may come up, suppose we have a rectangle and $u$ is the width of rectangle and $v$ the depth. Then the area is $a = uv$. Suppose $u$ and $v$ change in size with time, $x$.
Imagine a tennis court cover being unfolded:
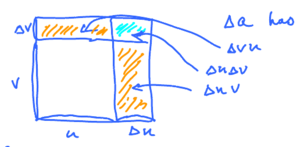
Grows in both directions. Suppose we know the rate of change of width, $u$, and depth, $v$. What is the rate of change of area, $a$? We need to compute: $$ \Delta a = \Delta (uv)$$
$a$ in time $x$, changes from $a$ to $a + \Delta a$:
- Width from $u$ to $u + \Delta u$.
- Depth from $v$ to $v + \Delta v$.
What is $\Delta a = \Delta (uv)$? Lets express it in terms of $\Delta u, \Delta v$. $\Delta a$ has 3 parts. What are they?
So $\Delta (uv) = \Delta u\cdot v + \Delta v \cdot u + \Delta u \cdot \Delta v$. Algebra: $$ \begin{aligned} \frac{d(uv)}{dx} = \lim_{\Delta x \to 0} \frac{\Delta (uv)}{\Delta x} &= \text{substitute} \\ & = \lim_{\Delta x \to 0} \frac{\Delta u\cdot v + \Delta v\cdot u + \Delta u\cdot \Delta v}{\Delta x} \\ & = \lim_{\Delta x \to 0} \left( \frac{\Delta u}{\Delta x}\cdot v + \frac{\Delta v}{\Delta x}\cdot u + \frac{\Delta u}{\Delta x}\cdot \Delta v \right) \\ & \overset{\text{SR}}{=} \lim_{\Delta x \to 0} \left( \frac{\Delta u}{\Delta x}\cdot v \right) + \lim_{\Delta x \to 0} \left( \frac{\Delta v}{\Delta x}\cdot u \right) + \lim_{\Delta x \to 0} \left( \frac{\Delta u}{\Delta x}\cdot \Delta v \right) \\ & \overset{\text{CMR}}{=} v \lim_{\Delta x \to 0} \frac{\Delta u}{\Delta x} + u \lim_{\Delta x \to 0} \frac{\Delta v}{\Delta x} + \lim_{\Delta x \to 0} \left( \underbrace{\frac{\Delta u}{\Delta x}}_{\frac{du}{dx}}\cdot \underbrace{\Delta v}_{0} \right) \\ & = v \cdot \frac{du}{dx} + u\frac{dv}{dx} + 0 \end{aligned} $$ So we have
Product Rule. $$ \frac{d}{dx} (uv) = v\frac{du}{dx} + u\frac{dv}{dx}. $$
Test the units: $$\frac{\text{ft}^{2}}{\text{sec}} = \text{ft}\cdot \frac{\text{ft}}{\text{sec}} + \text{ft}\cdot \frac{\text{ft}}{\text{sec}}$$ It works!
Example:
$$ y = xe^{x} $$ where $$ \begin{aligned} u & = \color{maroon}{x} \to \frac{du}{dx} = (x)^{\prime} = \color{green}{1} \\ v & = \color{green}{e^{x}} \to \frac{dv}{dx} = (e^{x})^{\prime} = \color{maroon}{e^{x}}. \end{aligned} $$ Apply PR via "cross-multiplication" the idea of which comes from the picture above: $$\frac{dy}{dx} = \color{maroon}{x\cdot e^{x}} + \color{green}{e^{x}\cdot 1} = e^{x}(x + 1).$$
What's behind the notation:
$$ y= \underbrace{f(x)}_{\text{name of function}} \quad \text{vs.} \quad y = \underbrace{x^{2}}_{\text{all we need}} $$
$$ \underbrace{(x^{2})^{\prime} = 2x}_{\text{shorter}} \qquad \underbrace{f(x) = x^{2} \to f^{\prime}(x) = 2x}_{\text{long}} $$
Instead of concentrating on the functions we can concentrate on the variables. Instead of $$ f^{\prime}(x) = 2x \gets f(x) = x^{2} $$ We use $$ y^{\prime} = 2x \gets y = x^{2} $$ or $$ \frac{dy}{dx} = 2x $$ Where does it come from? $$ \frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \begin{cases} \to & \text{ change of } y \\ \to & \text{ change of } x \end{cases} $$ if $y = f(x)$ then $$ \begin{aligned} \Delta y & = f(a+h) – f(a) \\ \Delta y & = h \end{aligned} $$
Re-write:
Sum rule Let $u = u(x), v = v(x)$ and let $y = u + v$. Then $$ \underbrace{\frac{d}{dx} (u + v)}_{\text{derivative of variable}} = \frac{du}{dx} + \frac{dv}{dx} $$
Continue to Differentiation without limits: part 3.