This site is being phased out.
PageRank: testing
An example
If $E$ is the set of edges of a directed graph and $N$ the total number of nodes in the graph then the PageRank of the $i$-th node is: $$P_i=(1-\epsilon )\sum _{(i,j)\in E}\frac{P_j}{d_j}+\frac{\epsilon }{N},$$ where $\epsilon$ is the damping coefficient and $d_j$ is the degree of node $j$.
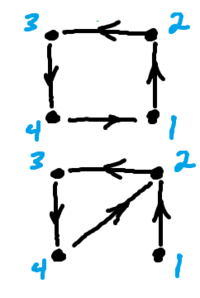
Suppose we have a circular directed graph as in the picture on the right. From the symmetry it follows that the page ranks of all the nodes should be equal. Since the PageRanks should add up to $1$, it follows that $$P_i=1/4,i=1,2,3,4.$$
Now, suppose whoever controls node 4 changes the link from 1 to 2. Then we have the second graph on the right. Then $$P_1=(1-\epsilon )[0]+\epsilon /4, $$ $$P_2=(1-\epsilon )[P_4+P_1]+\epsilon /4, $$ $$P_3=(1-\epsilon )[P_2]+\epsilon /4, $$ $$P_4=(1-\epsilon )[P_3]+\epsilon /4.$$ The result is a system of linear equations. One can plug this into Mathematica or similar algebra system to find the the exact solution. However, even without it we know that $$P_2>\epsilon /4=P_1.$$ So, someone who controls nodes 4 can move node 2 above node 1 at will.
The role of outlinks
They can improve your PageRank!
To experiment with ideas like this I've created this little spreadsheet. The formula comes from the original Page/Brin paper from 1998.
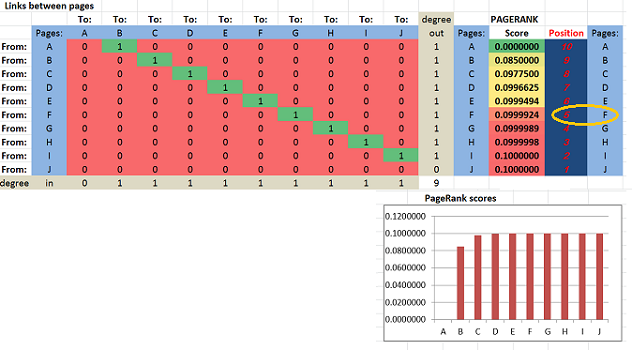
Suppose we have these ten "pages": A, B, ..., J. They are listed in the table as both rows and columns. The links are the entries in the table.
First we suppose that they link to each other consecutively: A → B → C → ... → J.
The PageRank scores, as well as the positions, of the pages are computed and displayed on the right. The scores for A, ..., J are increasing in the obvious way: from 0 to .1. In particular, F is #5.
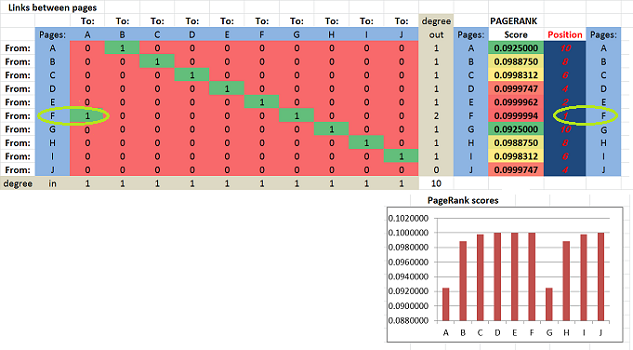
Next, suppose F adds a link to A: F → A. You can see that 1 has appeared in the first column of the table:
Now, suddenly F ranks first!
Yes, adding an outbound link has brought this page from #5 to #1.
The result certainly goes against our intuition. It shouldn't be surprising though considering other problems with the math of PageRank.
This isn’t a new discovery of course. These are just a couple of references for you:
- The effect of new links on Google PageRank by Konstantin Avrachenkov and Nelly Litvak, Stochastic Models, 22:319–331, 2006.
- Maximizing PageRank via outlinks by Cristobald de Kerchove, Laure Ninove, and Paul van Dooren, Linear Algebra and its Applications 429 (2008) 1254–1276.
The conclusion is that the appearance of a cycle is what seems to be the reason for this behavior...
You won't get a straight answer from Google on this. When asked to explain what PageRank is, they say it’s hardly a secret and refer you to the 1998 paper (or rehash its contents like here). However, if you criticize those ideas, the answer is: it's irrelevant because PageRank isn’t that anymore, it is now composed of 200 various "signals". So, what's PageRank anyway? Glad you asked, it's all explained in that famous paper from 1998...
Another cycle.