Orientation of manifolds

Introduction

In order to understand integration of $k$-forms over $k$-manifolds we need to learn about orientation of manifolds.

For $n$-manifolds, $n > 1$, we don't expect to find a single-function parametrization as we did with curves: $p \colon [a,b] \rightarrow C$. We'll have to deal with patches only, which makes things more complicated.

Informally, what is orientation?

Let's start with something related...

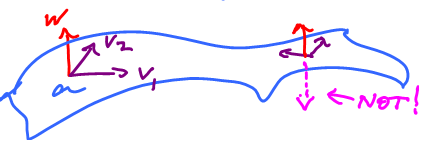
Orientability is the ability to move a normal vector around...

Here tangent vectors are: $v_1$, $v_2$. For surface $C$, a normal vector can be found by $w = v_1 \times v_2$, where $v_1$,$v_2 \in T_aM$. These form the basis of the tangent space at this point.

...without getting something else by accident.

What can go wrong?

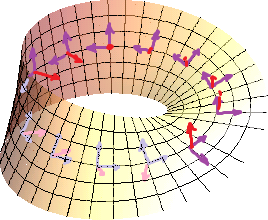
Consider the Mobius band.

It is not "orientable", because after a trip around you get the opposite normal!

Note: In topology, instead look at cells "oriented compatibly" (see Orientable surface).

Then

orientation is a certain way of moving the normal vector around

(there are only two).

Atlases of manifolds

To deal with the issue more formally, we use "patches" on the manifold.

There is a basis of the tangent plane at each point $a$, $b$, .... We want to get "compatible" bases for all patches. What does it mean?

A patch containing the point $a$:

Bow, where do the bases for all points in $U$ come from?

From the coordinate map (local parametrization) of the manifold: $$p \colon {\bf R}^n \rightarrow M, p({\bf R}^n)=U,$$ that's the patch.

How do we choose $\{p'(e_1), \ldots, p'(e_n)\}$ as a basis of $T_aM$?

First, none of these should be equal to 0.

Second, suppose $p$ is diffeomorphism with $p' \neq 0$. Consider

• a patch in $M$:

• then we get a basis of $T_aM$:

Same for any $b \in U$ (just like with curves).

If $a$ and $b$ are in the same patch, we can move along a curve from one to the other and directly compare the two bases.

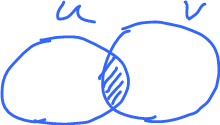
But what they are not in the same patch, what do we do when we reach the end of the patch?

Patches are open so if they intersect, they have to overlap!

Indeed, if $U \cap V \neq \emptyset$ then $U \cap V$ is open. Hence on $U \cap V$ there are two coordinate systems, from $U$ and from $V$. Do they agree?

They don't have to:

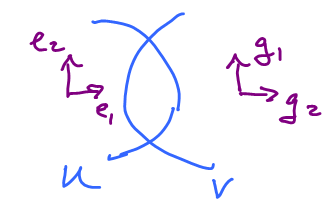
This is what we have: $$ \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} U & V \\ \ua{p} & \ua{q} \\ {\bf R}^n & {\bf R}^n, \end{array} $$ where $p$, $q$ are coordinate maps.

Then we also have this: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & & U \cap V & & \\ & & \nearrow _p \hspace{6pt} _q \nwarrow & & \\ & {\bf R}^n & \ra{ T=?} & {\bf R}^n \end{array} $$

We want to construct the missing part, $T$, from $p$ and $q$. How?

The diagram suggests the answer: let $$T = q^{-1}p.$$

It is simply a change of variables, again.

Assuming the parametrizations $p,q$ are diffeomorphisms, $T'$ exists and $T' \neq 0$.

How do we know the orientations agree?

Example: What if $T'(e_1)=g_2, T'(e_2)=g_1$?

That's what we mean by reversed orientation.

At this point it becomes clear that this is about linear algebra. Indeed the derivative $T'$ is a linear operator, $$T' \colon {\bf R}^n \rightarrow {\bf{R}^n}.$$

And what we know from linear algebra, for a linear operator $L$,

• if $\det L > 0$, it preserves orientation,
• if $\det L < 0$, it reverses orientation.

So, if $\det T' > 0$, we say that $U$ and $V$ agree on $U \cap V$.

Recall $\det T'$ is called the Jacobian.

Given a manifold $M$, an atlas is a set of patches that cover $M$.

The atlas is oriented if the change of variables between any pair of patches has a positive Jacobian.

Then manifold $M$ is called orientable if it has an oriented atlas.

Examples

Example (dimension $1$):

The circle as a boundary-less 1-manifold, a closed curve:

Note: The single function parametrization via polar coordinates fails to be an atlas (Why?).

Also not closed:

Both need two patches.

Example (dimension $2$):

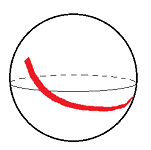
The sphere:

There is a single parametrization via spherical coordinates: rectangle $\rightarrow {\bf R}^3$.

But in that case there are points with two preimages, so you can't use this function to have a single patch. You'd need at least two patches: e.g.,

• ${\bf S}^2 \smallsetminus N$ and ${\bf S}^2 \smallsetminus S$ (the poles cut out).

Note: The combination of the north hemisphere and south hemisphere does not work, since they are closed, and if you open them, the equator is missing.

But slightly expanded hemispheres do work. Verify that you can have orientations of $U$, $V$ that agree.

Example: What about the Mobius band? The following fails: For any two points $A$,$B \in M$, there is a path between them so that bases of the tangent spaces along the path agree with each other.

Exercises

1. Prove that the Mobius band isn't orientable.

2. Provide an atlas of an $n$-sphere. What's the smallest one?

3. Provide an atlas of the torus.

4. Fix a subspace $W=R^{n-1}$ in $V=R^n$. Take a vector $q \in V - W$ and two bases $\{v_1, ..., v_{n-1}\}, \{u_1, ..., u_{n-1}\}$ of $W$. Prove that these bases agree on $W$ if and only if the bases $\{q, v_1, ..., v_{n-1}\}, \{q, u_1, ..., u_{n-1}\}$ agree on $V$.