Multiparameter filtrations

Multiparameter filtrations come from the same main sources as one-parameter filtrations.

First, color images:

are thresholded according to their three color channels;

Besides color images, parametrized images come from video analysis and object tracking, morphological analysis, and thermal imaging.

Second, point clouds are "thresholded" by the closeness of their points and, for example, the density of the points.

Let's limit our attention to the two-parameter case. A (finite) two-parameter filtrations $\{K^{nm}\}$ is a table of complexes connected by inclusions \begin{equation*} i(n,m,n+p,m+q):K^{nm}\rightarrow K^{n+p,m+q},p,q\geq 0, \end{equation*} These inclusions generate homomorphisms \begin{equation*} i_{\ast }(n,m,n+q,m+p):H_{\ast }(K^{nm})\rightarrow H_{\ast }(K^{n+q,m+p}), \end{equation*} with $0$s added in the end of each row and each column. Define the homology group of the filtration $\{K^{nm}\}$ as \begin{eqnarray*} H_{\ast }(\{K^{nm}\}) = {\displaystyle\bigoplus\limits_{n}}\ker i_{\ast }(n,m,n+1,m)\cap \ker i_{\ast}(n,m,n,m+1). \end{eqnarray*} The analogues of the results about the single parameter filtrations hold.

There are many ways to define persistence in the multiparameter setting.

For example, we can evaluate the robustness of a homology class $x\in H_{\ast}(K^{nm})$ in terms of the pairs $(p,q)$ of positive integers satisfying \begin{equation*} i_{\ast }(n,m,n+p,m)(x)=0\text{ and }i_{\ast }(n,m,n,m+q)(x)=0. \end{equation*}

Next, just as before, we restrict the homomorphisms generated by the inclusions to the homology classes of low persistence: \begin{eqnarray*} i_{\ast }(n,m,n+1,m):\ker i_{\ast }(n,m,n+p,m) &\rightarrow &\ker i_{\ast }(n+1,m,n+1+p,m), \\ i_{\ast }(n,m,n,m+1):\ker i_{\ast }(n,m,n,m+q) &\rightarrow &\ker i_{\ast }(n+1,m,n,m+1+q). \end{eqnarray*} Then the $(p,q)$-noise group of $K^{nm}$ is defined via these homomorphisms: \begin{eqnarray*} N_{\ast }^{pq}(\{K^{nm}\}) = {\displaystyle\bigoplus\limits_{n}}\ker i_{\ast }(n,m,n+1,m)\cap \ker i_{\ast }(n,m,n,m+1). \end{eqnarray*} Finally, the $(p,q)$-persistent (homology) group of filtration $\{K^{nm}\}$ is defined as \begin{equation*} H_{\ast }^{pq}(\{K^{n}\})=H_{\ast }(\{K^{nm}\})/N_{\ast }^{pq}(\{K^{nm}\}). \end{equation*}

The results about $H_{\ast }^{pq}(\{K^{nm}\})$ analogous to the ones about $H_{\ast }^{p}(\{K^{n}\})$ hold.

Alternatively, we can use only the persistence with respect to one of the parameters: \begin{eqnarray*} N_{\ast }^{p}(K^{nm}) &=&\ker i_{\ast }(n,m,n+p,m)\text{ or} \\ N_{\ast }^{p}(K^{nm}) &=&\ker i_{\ast }(n,m,n,m+p). \end{eqnarray*} Or diagonally $$N_{\ast }^{p}(K^{nm})=\ker i_{\ast }(n,m,n+p,m+p).$$

More generally, suppose $I$ is a poset equipped with a pseudometric $d:$

• $d(x,x)=0,$
• $d(x,y)=d(y,x),$
• $d(x,z)\leq d(x,y)+d(y,z).$

Then we say that an element $x\in H_{\ast }(K^{n})$ has persistence $P(x)=p$ if $i_{\ast }^{nm}(x)=0$ for all $m>n$ such that $d(n,m)\geq p,$ and $i_{\ast }^{nM}(x)\neq 0$ for some $M$ with $d(n,M)=p.$ In other words,

• $P(x)=\max \{p:i_{\ast }^{nm}(x)\neq 0 \}$ for some $m\geq n$ such that $d(n,m)=p$.

In the first example above $$d((x,y),(a,b))=\max \{|x-a|,|y-b|\}.$$

Exercise: Show that the triangle inequality guarantees that this notion makes sense.

Proposition. (Monotonicity) If $P(x)\leq P(y)$ then $P(i_{\ast }^{nm}(x))\leq P(i_{\ast}^{nm}(y)),$ for $x,y\in H_{\ast }(K^{n}).$

Definition. For any $n\in I$ and any real $p$ define the $p$-noise homology group of $K^{n}$ as $$N_{\ast }^{p}(K^{n})=\bigcap \{\ker i_{\ast }^{nm}:d(n,m)\leq p\}.$$

As before, a new direct system is well defined: $$N_{\ast }^{p}(K^{n})\rightarrow N_{\ast }^{p}(K^{m}),\text{ for }n\leq m,$$ where the homomorphisms are simply the restrictions of $\,i_{\ast }^{n,m}$ on $N_{\ast }^{p}(K^{n}).$ We extend the definitions above.

Definition. Given a positive integer $p,$ the $p$-noise (homology) group $N_{\ast }^{p}(\{K^{n}\})$ of filtration $\{K^{n}\}$ is the product of the direct system $\{N_{\ast }^{p}(K^{n}),i_{\ast }^{n,m}\}:$ $$N_{\ast }^{p}(\{K^{n}\})=\bigoplus\limits_{n}\bigcap\limits_{m\geq n}N_{\ast }^{p}(K^{m}),$$ and the $p$-persistence group is $$H_{\ast }^{p}(\{K^{n}\})=H_{\ast }(\{K^{n}\})/N_{\ast }^{p}(\{K^{n}\}).$$

Exercise. How can it be defined axiomatically?

Functoriality...

We need to understand how maps of filtrations affect their homology. These maps are well defined if the filtrations have the same number of elements (1-parameter). To understand the affect of noise on images and data we need also include insertions, deletions, copying etc.

To this end, it would be preferable to define the homology of the filtration "functorially". Recall, if we have a poset $I$ and a collection of complexes indexed by $I$: $$\{K^{n}\}_{n\in I}$$ and inclusions $i^{nm}:K^{n}\rightarrow K^{m}$ for all $n\leq m,$ then the homology group of filtration $\{K^{n}\}$ is: $$H_{\ast }(\{K^{n}\})=\bigoplus\limits_{n}\bigcap\limits_{m\geq n}\ker\,i_{\ast }^{nm}.$$

The definition is confined to the category of abelian groups. More generally, we have a direct system in an arbitrary category $C$: $$f^{nm}:X^{n}\rightarrow X^{m},$$ where $n\leq m$ belong to some poset $I.$ Then we can define the product of this direct system as $$\prod \{X^{n},f^{nm}\}=\bigoplus\limits_{n}\bigcap\limits_{m\geq n}\ker \,f^{nm}.$$

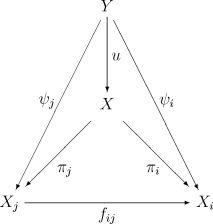
Theorem [Universal Property]. The product of system $\{X_{i}\}$ (modulo $\{f_{ij}\})$ is an object $X$ in $C$ together with morphisms $\pi _{i}:X\rightarrow X_{i}$ (called projections) satisfying $f_{ij}\circ \pi _{i}=0$. The pair $(X,\pi _{i})$ must be universal in the sense that for any other such pair $(Y,\psi _{i})$ there exists a unique morphism $u:Y\rightarrow X$ making all the "obvious" identities true; i.e., the diagram below commutes