More on vector spaces

Besides Euclidean spacees, another important class of examples of vector spaces is...

Function spaces

Observation: There are algebraic operations on functions $f \colon {\bf R} \rightarrow {\bf R}$:

• addition,
• subtraction,
• multiplication,
• division.

But we will ignore the last two, for now.

Let $V$ be the set of all functions $f \colon {\bf R} \rightarrow {\bf R}$.

Note: The difference in the meaning of this notation is that, in Calc 1, this means that domain $f \subset {\bf R}$ and here domain $f={\bf R}$.

Let's define operations on $V$.

Keep in mind the notation:

• $f$ represents the function as a whole, and
• $f(x)$ represents its value at $x$.

Let's define addition on $V$.

Given $f,g \in V$, what is $h=f+g \in V$?

Note: we know how to add numbers but not functions yet!

How?

We simply need to know $h(x)$ for each $x$. Here it is:

• $h(x)=f(x)+g(x)$ for each $x \in {\bf R}$.

Define scalar multiplication on $V$ now.

We need to know, given $f \in V$, $r \in {\bf R}$, what is $h=rf$? Here:

• $h(x)=rf(x)$ for each $x \in {\bf R}$.

Exercise: Verify the axioms. (How? Entry-wise, input-wise: for each $x$, $f(x) \in {\bf R}$. ${\bf R}$ is a vector space! Use it.)

What about other vector spaces of functions?

How about we narrow it down. We suppose $f$ is continuous. Then we have same operations.

But, we have to ask: is the set closed under these operations?

Recall from Calculus 1: course.

Theorem: The sum of two continuous functions is continuous.

Theorem: The product of a number and a continuous function is continuous.

Where do these come from? From theorems about limits: sum rule and constant multiple rule.

So, $C({\bf R})$ is closed under these operations.

How about $C^1({\bf R})$, differentiable functions (or integrable, etc). Make your own examples.

Example: Let $V = \{ f \in C({\bf R}) \colon f(0)=0 \}$ .

Is it closed under the operations above?

Given $f,g \in V$. Then

• #1. $(f+g)(0) = f(0)+g(0) = 0+0 = 0$, so $f+g \in V$.
• #2. $(cf)(0) = cf(0) = c \cdot 0 = 0$, so $cf \in V$.

Yes!

Subspaces

We need closedness to have a vector space, but is closedness sufficient?

Not in general, you need the axioms too.

But what about specifically subsets of vector spaces?

Look at ${\bf R}^2$. What are possible vector spaces that exists as subsets of ${\bf R}^2$?

One answer is: all straight lines through $0$.

Let $V = \{ (x,y) \in {\bf R}^2 \colon y=mx\}$.

For closedness consider:

• $(x,y), (a,b) \in V \rightarrow y=mx, b=ma$, then $(x,y)+(a,b) = (x+a,y+b)$.

Do they satisfy the equation?

• $y+b=m(x+a)$,

yes!

Same for scalar multiplication.

But what about the axioms?

Geometrically, they are satisfied clearly. Just, compare $V$ and ${\bf R}$:

You have to look at the magnitudes only.

The operations look very similar! This suggests that $V$ satisfies the axioms, just as ${\bf R}$ does.

Theorem: Given a vector space $U$, and a subset $V$ of $U$. Also assume:

• 1. $0 \in V$,
• 2. $V$ is closed under addition of $U$,
• 3. $V$ is closed under scalar multiplication of $U$.

Then $V$ is a vector space.

Proof: 2. and 3. mean the operations make sense on $V$.

Recall the definition of vector space. The axioms:

• 1. $u+v=v+u$
• 2. $(u+v)+w = u+(v+w)$
• 3. There is a vector $0 \in V$ such that $0+a=a$ for all $a \in V$.
• 4. For each $a \in V$, there is a vector $-a \in V$ such that $a + (-a)=0$.
• 5. $r(u+v)=ru+rv$
• 6. $(r+s)u = ru+su$
• 7. $(rs)u = r(su)$

Let's check them each.

• #1. Given $u,v \in V$, then $u,v \in U$, so since $U$ is a vector space, it satisfies #1. So $u+v=v+u$, within $U$ by condition 2 (note $u$ and $v$ are in $V$). But also within $V$... we never leave $V$.
• #2. Same argument.
• #3. Let the identity of $V$ be $0$ (the identity of $U$); it's ok by condition 1.

$0+a=a$ for all $a \in U$, since $U$ is a vector space. Hence $0+a=a$ for all $a \in V$, since $V \subset U$.

• #4. Given $a \in V$, we need to define an element $-a \in V$ such that $a + (-a) = 0$. Choose as $-a$, the inverse of $a$ in $U$. It's ok because $-a \in V$. Why? Use one of the properties: $-a=(-1)a$, scalar multiplication. So by condition 3, $(-1)a \in V$.
• #5-8. Proven by using conditions 2 and 3.

$\blacksquare$

Can we drop some of the conditions of the theorem? Will it still hold?

Let's try.

What if $0 \not \in V$?

Consider $V = \{(x,y) \colon y = x+1 \} \subset {\bf R}^2$ here $0 \not\in V$. This is not a vector space!

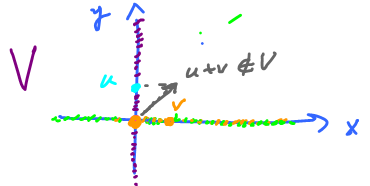
What if it's not closed under addition?

Let's try build it. Start, for example, with $v=(1,0)$. (Note: Such a vector exists because $\{0\}$ is a vector space, so there is at least one non-zero vector in $V$, $v$.)

Condition 3 is satisfied, so $2v, 3v, -v, \ldots \in V$, so the whole $x$-axis $\subset V$. But the $x$-axis is a vector space!

So, there should be a vector in $V \setminus \{x$-axis$\}$, $u$.

Condition 3 is satisfied, so the $y$-axis $\subset V$. Observe $u+v \not\in V$.

So, $V$ is not a vector space!

But it does satisfy 3. Hence we can't drop 2.

Note: the construction ends with $V = \{ (x,y) \colon x=0 {\rm \hspace{3pt} or \hspace{3pt}} y=0 \}$.

Exercise: Show that condition 2 can't be dropped.

Notation:

• ${\bf Z} = \{0, \pm 1, \pm 2, \ldots\}$;
• ${\bf Q} = \{ \frac{p}{q} \colon p, q \in {\bf Z}, q \neq 0 \}$

Quiz: Prove or disprove: ${\bf Q}$ is closed under addition.

Proof: Suppose $u,v \in {\bf Q}$, then $u=\frac{p}{q}$, $v = \frac{r}{s}$ for some $p,q,r,s \in {Z}$. Then $u+v = \frac{p}{q} + \frac{r}{s} = \frac{ps+rq}{qs}$. And here $ps+rq, qs \in {\bf Z}$. Hence $u+v \in {\bf Q}$.

Question: Is ${\bf Q}$ closed under scalar multiplication?

Answer: No, $\sqrt{2} \cdot 1 = \sqrt{2} \not\in {\bf Q}$.

Definition: A subset of a vector space that is also a vector space under its operations is called a subspace.

Issue: Subsets vs subspaces, sets vs vector spaces, i.e., they have extra structure (algebraic operations).

Big question: Suppose $V \subset W$, subset of a vector space. Is it a subspace, i.e., do 1-3 hold?

Restate the above theorem.

Subspace Theorem: A subset $V$ of a vector space $W$ is a subspace if $V$ contains $0$ and is closed under the algebraic operations of $W$.

This is a powerful tool to discover new vector spaces.

${\bf R}^2$, subspaces:

• all lines through $0$ (prove).

${\bf R}^3$, subspaces:

• 1. all lines through $0$,
• 2. all planes through $0$.

Point: To prove, no need to prove the axioms.

Other examples from recently:

• $F$ is the vector space of functions, then $C({\bf R})$, continuous ones, is a subspace.
• $C^1({\bf R})$ (differentiable) is as well.

All we need to show:

• 1. The sum of two continuous functions is continuous.
• 2. A constant multiple of a continuous function is continuous.

But we already know it from Calculus 1!

New example: all polynomials = ${\bf P}$ (exercise).

Consider $$P \subset C^1({\bf R}) \subset C({\bf R}) \subset F$$ They are subsets.

But they are subspaces too. In fact, these are "proper" subspaces: $A \subsetneq B$.

Example: In ${\bf M}(2,2)$, choose diagonal matrices, like: $A = \left[ \begin{array}{ccc} a & 0 \\ 0 & b \end{array} \right]$. Call it $D$. Is $D$ a subspace?

First, $\left[ \begin{array}{ccc} a & 0 \\ 0 & b \end{array} \right] + \left[ \begin{array}{ccc} c & 0 \\ 0 & d \end{array} \right] = \left[ \begin{array}{ccc} a+c & 0 \\ 0 & b+d \end{array} \right] \in D$.

Second, $r\left[ \begin{array}{ccc} a & 0 \\ 0 & b \end{array} \right] = \left[ \begin{array}{ccc} ra & 0 \\ 0 & rb \end{array} \right] \in D$. Yes!

Exercise: Prove or disprove that the intersection of two subspaces is a subspace.

Question: Is the union of two subspaces always a subspace?

Answer: No.

Counterexample:

• $U = \{x$-axis$\}$ and
• $V = \{y$-axis$\}$

are subspaces of ${\bf R}^2$.

Consider, $U \cap V = \{0\}$ is a subspace, but $U \cup V$ is not a subspace, since $(1,0) \in U$ and $(0,1) \in V$ but $(1,0)+(0,1)=(1,1) \not\in U \cup V$.

Question: What about subspaces in ${\bf R}$? There is no example. Subspaces of ${\bf R}$ are $\{0\}$ and ${\bf R}$ itself, and only these two!

(Note: The irrationals is not a subspace: $\sqrt{2}\sqrt{2} = 2$ and $\sqrt{2} - \sqrt{2}=0$.)

A rich source of examples of subspaces in the Euclidean space is...

Lines

Some of these are subspaces of ${\bf R}^2$ and ${\bf R}^3$. This is what we know:

Theorem: A straight line in ${\bf R}^2$ is a subspace if and only if it contains $0$.

Proof: We did ($\Leftarrow$) earlier. Next, to do ($\Rightarrow$) we observe that the definition requires that a vector space contains $0$. $\blacksquare$

Let's be careful here. We know lines as $y=mx+a$, with $m$ the slope. They pass through $0$ if $a=0$. However, this representation omits vertical lines! We need to resole this before we generalize the idea to abstract vector spaces.

Suppose $V$ is a vectors space, what is a line in a vector space?

To get the idea, go back to Calculus 2 and Calculus 3, specifically parametric curves.

A straight line is a parametric curve:

$\left\{ \begin{array}{rl} x=t \\ y=mt \end{array} \right\}$,

but once again no vertical lines here?

Better:

$\left\{ \begin{array}{rl} x=rt \\ y=st \end{array} \right\}$,

Here $r,s \in {\bf R}$ are fixed, and we assume that not both are $0$. Note: $t \in {\bf R}$ parameter (you can think of $t$ as time).

Then we can rewrite $$(x,y) = (rt,st)$$ as vectors.

What is the meaning of $r$ and $s$?

They determine the direction (the angle) of the line. In fact, $(r,s)$ is a vector and it's called the direction the vector of the line.

So the line is, $$(x,y)=t(r,s)$$ (here $t$ is a variable, and $(r,s)$ is fixed).

Observe that vector $(x,y)$ is always proportional to $(r,s)$, therefore they have the same direction.

Definition: Given a vector space $V$ and a non-zero vector $v$. Then the set $$L=\{tv \colon t \in {\bf R}\}$$ (all multiples of $v$) is called the line in the direction of $v$.

Theorem: For $v \neq 0$, a line $L$ in the direction of $v$ is a subspace.

Proof: Let $u,w \in L$. Then $u=tv$, for some $t \in {\bf R}$, and $w = sv$, for some $s \in {\bf R}$. Then $u+w=tv+sv=(t+s)v \in L$, since $t+s \in {\bf R}$. So $L$ is closed under addition. Scalar multiplication -- exercise. $\blacksquare$

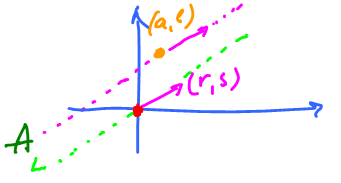
Also, given $w \in V$, $A = \{u = w + tv \colon t \in {\bf R}\}$ is called the line through $w$ in the direction of $v \neq 0$.

Recall, every line in ${\bf R}^2$ is given by $$(x,y) = (a,b)+t(r,s).$$ The idea comes from the motion interpretation: $(a,b)$ is the initial location and $(r,s)$ is the direction of the motion.

We already know this

Fact: $A$ is a subspace if $(a,b)=0$.

Exercise: What about "only if"?

• $A$ is also called an affine subspace.
• $L$ is also called a linear subspace.

Another example, in space, is...

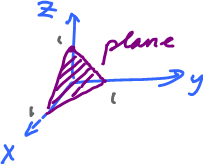
Planes

We start in ${\bf R}^3$.

We already know that $x+y+z=1$ is not a subspace.

Instead consider $x+y+z=0$, then this is a subspace: $$P = \{(x,y,z) \in {\bf R}^3 \colon x+y+z=0\}.$$

In general, $$P \colon Ax + By + Cz =0,$$ gives all planes through $0$, provided not all $A,B,C = 0$.

Theorem: $P$ given above is a subspace.

Proof: Exercise.

This is coordinate dependent though.

Just like with lines, let's find a parametric representation. This is called parametric surfaces. Compare these two.

• Multiples of $v$, $L = \{ \alpha v \colon \alpha \in {\bf R} \}$:

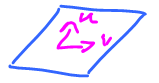
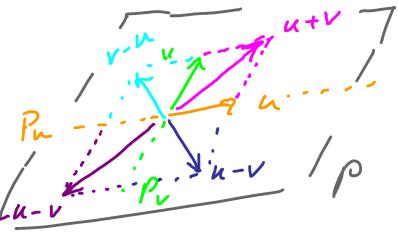
• Combinations of $u$ and $v$, $P = \{\alpha u + \beta v \colon \alpha, \beta \in {\bf R} \}$):

Definition: Given two vectors $u,v$ that are not multiples of each other, then define $$P = \{ \alpha u + \beta v \colon \alpha, \beta \in {\bf R}\}$$ as the plane in the direction of $u,v$.

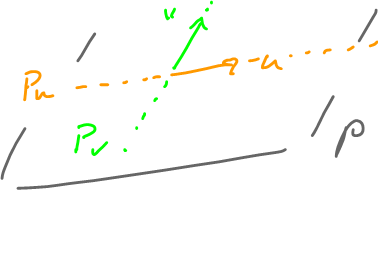
Consider these subsets

• $P_u = \{ \alpha u \colon \alpha \in {\bf R} \}$, a line in the direction of $u$ and
• $P_v = \{ \beta v \colon \beta \in {\bf R} \}$, a line in the direction of $v$.

What if $u = \lambda v$?

Then $P$ is a line: $$\alpha u + \beta v = \alpha \lambda v + \beta v = (\alpha \lambda + \beta) v.$$ Since $\alpha \lambda + \beta \in {\bf R}$ we get all multiples of $v$.

So, in this case, $P$ is the line in the direction of $v$.

In general, start with the two lines...

A lot more here than that. Indeed, we add more and more vectors to fill in the plane:

Theorem: $P$ above is a subspace of ${\bf R}^3$.

Definition: $$P = \{(x,y,z) = w+\alpha u + \beta v, \alpha, \beta \in {\bf R} \}$$ is called the plane through $w$ in the direction of $u,v$, where $w,u,v \in V$, a vector space.

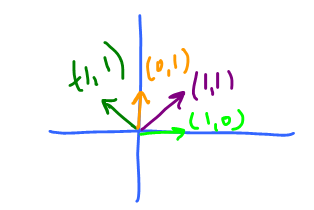
Example: Consider $$V = {\bf C}({\bf R}), w=3, u = x,v=x^{2}.$$

Then the elements of $P$ are: $$q = w+\alpha u + \beta V= 3 + \alpha x + \beta x^2,$$ with $\alpha, \beta \in {\bf R}.$ (Note: $x \in {\bf R}$ is a variable here.)

What is $V$, as a set?

It is the set of all quadratic polynomials with free term $=3$.

Quiz: Let $V$ be space of all polynomials and $S = \{ p \in V \colon p(\sqrt(2))=0 \}$. Prove $S$ is a vector space.

By the theorem, verify 3 conditions

• 1. $S \neq 0$. Choose the zero polynomial.
• 2. Closed under addition, $p,q \in S$ implies $p(\sqrt{2})=0$ and $q(\sqrt{2})=0$, so $p+q \in S$ (note: instead of $p(x), q(x)$!).

Consider $(p+q)(\sqrt{2}) = p(\sqrt{2})+q(\sqrt{2}) = 0+0 = 0$, so $p+q \in S$.

• 3. Closed under scalar multiplication: $p \in S$, $r \in {\bf R}$ implies $p(\sqrt{2})=0$ and so $rp \in S$.

Consider $(rp)(\sqrt{2}) = rp(\sqrt{2}) = r \cdot 0 = 0$, so $rp \in S$.

Homework:

Let $V$ be the vector space of all polynomials and $T = \{ p \in V \colon p(\sqrt{2}) = 0$ and $p(\pi) = 0 \}$. Prove that $T$ is a vector space.