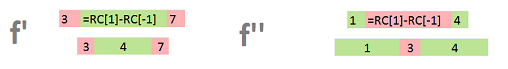More metric complexes

Hodge-dual complexes

Let's recall the mechanical interpretation of a realization $|K|$ of a metric complex $K$ of dimension $n=1$:

• the edges are rods and the vertices are hinges. $\\$

Furthermore, we connect the centers of the adjacent rods using an extra set of rods (and hinges) that form a new, Hodge-dual, complex $K^{\star}$.

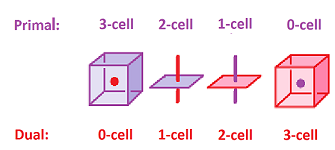
Given now a cell complex $K$ of an arbitrary dimension, the first step in the construction its dual $K^\star$ is to choose the dimension $n$. The rule remains the same:

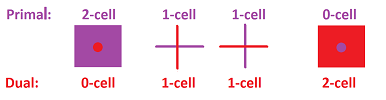
• each primal/dual $k$-cell $\alpha$ corresponds to a dual/primal $(n-k)$-cell $\alpha^\star$.

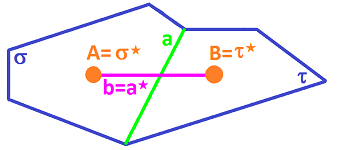
First we consider the case of $n=2$:

For the illustrations below, we will assume that each primal cell and its dual are directly “linked” in the realization, as follows:

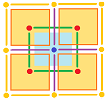
• If $\alpha$ is a $2$-cell then $\alpha^{\star}$ is a $0$-cell located at the “center” of $\alpha$.
• If $a$ is a $1$-cell then $a^{\star}$ is a $1$-cell crossing at the “center” of $a$.
• If $A$ is a $0$-cell then $A^{\star}$ is a $2$-cell centered at $A$. $\\$

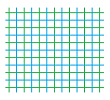
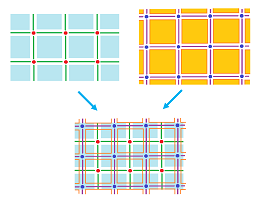
The result is a “staggered” grid of tile-like cells. It is simple for ${\mathbb R}^2$, as well as for any rectangular grid:

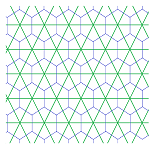
Other decompositions of the plane produce more complex patterns:

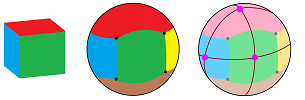
For the $2$-cells, their duals are their centers, the $0$-cells. We see below how these squares shrink to become the dots.

Meanwhile, the $0$-cells are blown into the squares. Finally, the duality makes every $1$-cell turn $90$ degrees around its center.

It is easy to illustrate the Hodge duality in a spreadsheet: one simply resizes the rows and columns in order to make the narrow cells wide and the wide cells narrow:

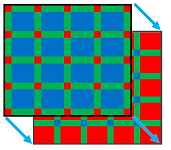
That's how you could build the dual of the whole-plane complex -- following this one-to-one correspondence. Furthermore, you can rebuild the primal complex from the dual following the same procedure. Below, we show a primal grid, the dual grid, and then the two overlapping each other:

What happens if we have a finite cubical complex $K$ in ${\bf R}^2$? Just as in dimension $1$, some boundary cells are missing in the dual complex, as the example shows:

Then, in general, $$K^{\star\star} \ne K.$$

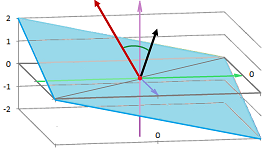
There is more going on in ${\bf R}^3$:

The $k$-cells and the $(n-k)$-cells are still paired up.

Exercise. Express the dual cell of a cube $Q$ in ${\mathbb R}^N$ in terms of its primal via the orthogonal complement construction.

Exercise. What is the Hodge dual of ${\mathbb R}^2$ in the ${\mathbb R}^3$?

Exercise. In ${\mathbb R}^n$, each $k$-cube $Q$ is represented as the product of $k$ edges and $n-k$ vertices. Find such a representation for $Q^\star$.

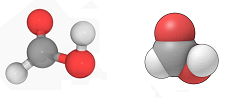
Example (molecule). To illustrate the idea of duality in dimension $3$, one may consider the two ways a chemist would construct a model of a molecule:

The two equally valid ways are:

• small balls connected by rods, or
• large balloons pressed against each other. $\square$

Exercise. Describe the cells in the above example.

Exercise. Two polyhedra are called dual if the number of faces of one is equal to the number of vertices of the other (and vice versa). Find the dual polyhedra of Platonic solids and explain the relation to the Hodge duality:

This is what the Hodge duality looks like in the case of a general $2$-dimensional cell complex. The dual cell is still placed -- for the sake of illustration -- at the center of mass of the primal cell:

Exercise. Suppose a simplicial complex $K$ is realized in ${\bf R}^n$. Describe explicitly how the dual $K^\star$ can also be realized in ${\bf R}^n$ side by side with $|K|$. Hint: use barycentric coordinates.

We summarize the new concept as follows.

Definition. Suppose a dimension $n$ is given. Two cell complexes $K$ and $K^\star$ with $\dim K \le n$, $\dim K^\star \le n$, are called Hodge-dual of each other if there is a one-to-one correspondence, $$K \ni a \longleftrightarrow a^\star \in K^\star,$$ between their cells of complementary dimensions: $$\dim a^\star+\dim a = n.$$

Metric complexes

We have already seen metric complexes of dimension $n=1$ as cell complexes equipped with a geometric structure: the metric tensor of $K$ and $K^\star$. This data allows one to find the lengths and the curvatures of curves. The Hodge star operator is then built from this data.

In this subsection, we present the necessary geometric data for the case of arbitrary dimension.

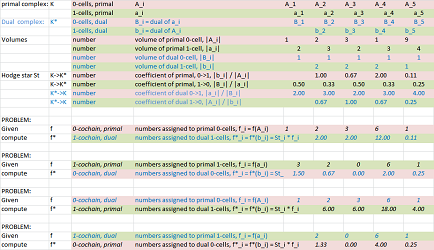
In dimension $n=2$, we consider lengths and areas; in dimension $n=3$, lengths, areas, and volumes, etc. In general, we need to find the “sizes” of all cells of all dimensions in the complex. These sizes are called the $k$-dimensional volumes: $$\begin{array}{c|c|c} \text{dimension } k& k\text{-cell } a& k\text{-volume } |a|\\ \hline 0 & \text{vertex} & 1\\ 1 & \text{edge} & \text{length}\\ 2 & \text{face} & \text{area}\\ 3 & \text{solid} & \text{volume}\\ ...& &...\\ n & n\text{-cell} & n\text{-volume}\\ \hline \end{array}$$

Instead of trying to derive these quantities from the metric tensor, we simply list them as a part of the definition of a metric complex. In the abstract, we simply have a pair of positive numbers $|b|,|b^\star|$ assigned to each cell $b\in K$.

Definition. Given a cell complex $K$, the volume function on $K$ defines the $k$-volumes of the $k$-cells of $K$: $$|\cdot |:K \to R\setminus \{0\},$$ normalized for dimension $0$: $$|A|=1 \ \text{ for all vertices } A \in K.$$

For $R={\bf R}$, the definition matches the one for the case of $n=1$ considered previously if we limit ourselves to positive volumes.

Example. The simplest choice of the volumes for the $2$-cell representation of the sphere is $$\hspace{.34in} A^0,a^2 \text{ with } |A^0|=|a^2|=1. \hspace{.34in}\square$$

In general, we don't assume that $|AB|,|BC|,|CA|$ determine $|ABC|$. Even though the three sides of a triangle determine the triangle and, therefore, its area, this only works under a particular choice of geometry, such as Euclidean. We take the opposite approach and let the lengths and areas determine the geometry.

Exercise. Give a metric complex representation of a triangulation of the sphere, realized as the unit sphere in ${\bf R}^3$.

Example (measure). Suppose $K$ is a cell complex with finitely many cells at each vertex and suppose $|K|$ is its realization. Then the set of all cells (open or closed) $\Sigma$ of $K$ as subsets of $|K|$ form a $\sigma$-algebra, i.e., a collection closed under the operations of complement, countable union, and countable intersection. If, furthermore, $K$ has a volume function, the function $\mu :\Sigma \to {\bf R}\cup \{\infty\}$ given by $$\mu(a)=\begin{cases} |a| & \text{ if } \dim a =\dim K,\\ 0 & \text{ if } \dim a <\dim K, \end{cases}$$ is a measure on $|K|$; i.e., it satisfies:

• non-negativity: for all $a\in \Sigma$ we have $\mu(a)\ge 0$;
• null empty set: $\mu(\emptyset) = 0$;
• $\sigma$-additivity: for all countable collections $\{a_i\}$ of pairwise disjoint sets in $\Sigma$ we have:

$$\hspace{.37in} \mu\Big(\bigcup_{k=1}^\infty a_k\Big)=\sum_{k=1}^\infty \mu(a_k). \hspace{.37in}\square$$

In addition to the volumes, the angles between every pair of dual cells will be taken into account in the new representation of the geometry.

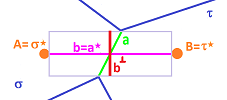
We don't need to specify the meaning of the angle between every choice of a primal $k$-cell and its dual $(n-k)$-cell, for all $k$. For our purposes, it suffices to take care of the case $k=1$. We are then in a familiar situation because the angle $\alpha$ between $1$- and $(n-1)$-dimensional subspaces of an $n$-dimensional inner product space is always understood as the angle between the direction vector of the former and the normal vector of the latter.

They are orthogonal when this angle is zero. It is also assumed that (for $k=0$) a point and the whole space are orthogonal and $\cos \alpha =1$. This assumption explains why these angles did not have to come into play in the case of a $1$-dimensional complex.

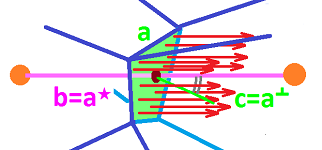
For cells in the higher dimensional case, we are looking at the angle between $a$ and the normal $b^\perp$ of $b=a^\star$, illustrated for dimension $n=2$:

Dually, this angle can also be understood as the angle between the normal $c=a^\perp$ of $a$ and $a^\star$, illustrated for dimension $n=3$:

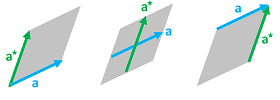
Even though these angles don't affect the volumes of either primal or dual cells, they do affect the volumes of new $n$-cells, the cells determined by each dual pair:

The area of this parallelogram does not depend on how $a$ and $a^\star$ are attached to each other (they aren't) but only on the angle between them.

The way we handle angles is, of course, via the inner product: $\langle a,b \rangle \in R$ is defined for these three cases:

• adjacent $a,b\in K$,
• adjacent $a,b\in K^\star$, and now also
• $a\in K,a^\star\in K^\star$.

Definition. A metric (cell) complex of dimension $n$ is a pair of Hodge-dual cell complexes $K$ and $K^\star$ of dimension $n$ equipped with a joint metric tensor, which is a combination of metric tensors for $K$ and $K^\star$ as well as inner products of all dual pairs: $$(a,a^\star)\mapsto \langle a,a^\star \rangle \in R.$$

Exercise. Represent a hollow cube as a metric complex. Hint:

Exercise. Suppose $K$ is a metric complex. Show how the set of its vertices $K^0$ becomes a metric space.

It follows from the definition that, in addition to the two volume functions of these complexes, we can also derive the angle function: $$(a,a^\star)\mapsto \cos\widehat{a a^\star}=\frac{\langle a,a^\star \rangle}{|a||a^\star|}.$$ The function is well-defined whenever the expression in the right-hand belongs to our ring $R$. This is always the case when $R$ is a field or $|a|=|a^\star|=1$.

Definition. We say that $K$ has a rectangular geometry if $$\langle a,a^\star \rangle =\pm |a||a^\star|.$$

In other words, all dual pairs are orthogonal: $$\cos\widehat{a a^\star}=\pm 1.$$ The case of $n=1$ previously considered is rectangular.

Definition. We will say that the complex $K$ has the standard geometry if it is rectangular and also fully normalized: $$|a|=1 \ \text{ for all cells } a\in K\sqcup K^\star.$$

We always assume that ${\mathbb R}^n$ has the standard geometry.

The Hodge star operator

We continue to take the concepts we have considered previously for the case of dimension $1$ and define them for the general case of dimension $n$. We define an operator from primal to dual chains that incorporate the geometry of the complex. Its formula is based on the analysis above.

Definition. The (chain) Hodge star operator of a metric complex $K$ of dimension $n$ is the pair of homomorphisms on chains of complementary dimensions: $$\begin{array}{lll} \star:C_k(K)\to C_{n-k}(K^\star ),& k=0,1, ...,n,\\ \star:C_k(K^\star)\to C_{n-k}(K),& k=0,1, ...,n, \end{array}$$ defined by $$\star (a):=\pm\frac{\langle a, a^\star \rangle}{|a^\star|}a^\star .$$ for any cell $a$, dual or primal, with the sign to be defined later.

The expression can be understood as the total flux of $a$ across a region of area $1$ on $a^\star$:

The two operators then satisfy: $$\star (a)|a^\star|=\langle a, a^\star \rangle =\star(a^\star) |a|$$

The following statements are easy to prove.

Proposition. The matrix of the Hodge star operator $\star$ is diagonal with: $$\star_{ii}=\pm\tfrac{|a_i|}{|a_i^\star|}\cos\widehat{a_i a_i^\star},$$ where $a_i$ is the $i$th cell of $K$.

Theorem. The two star operators are the inverses of each other, up to a sign: $$\star\star=\pm\operatorname{Id}.$$

Theorem. For a rectangular geometry, the Hodge star operator $\star$ preserves volumes of cells: $$|\star (a)|=|a|.$$

Proposition. The Hodge star operator is always well-defined when

• $R$ is a field, or
• the geometry of $K$ is standard.

Exercise. Provide the Hodge star operator for a metric complex representation of a triangulation of the sphere realized as the hollow unit cube in ${\bf R}^3$.

Exercise. Provide the Hodge star operators for the examples of metric tensors presented in this and the last sections.

Next, what happens to the forms under Hodge duality?

Definition. In a metric complex $K$, the Hodge-dual form $\psi^\star$ of a form $\psi$ over $K$ is given by $$\psi^\star(\sigma):=\psi(\sigma ^{\star}).$$

The operation is extended from cells to chains by linearity making these diagrams commutative: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccccccccc} &C_{k}(K)\ & \ra{\star} & C_{n-k}(K^\star) &&&C_{k}(K)\ & \la{\star} & C_{n-k}(K^\star) &&\\ &\ \ \da{\varphi} & &\ \ \da{\varphi^\star} && &\ \ \da{\psi^\star}& &\ \ \da{\psi} && \\ &R&= & R& &&R& =& R& & \end{array} $$ Then the formula is written for any chain: $$(\star \psi)(a):=\psi(\star a ),$$ where $\star$ in the right-hand side is the chain Hodge star operator.

Definition. The (cochain) Hodge star operator of a metric complex $K$ is the dual of the chain Hodge star operator ($\star=\star^*$); i.e., it is the pair of homomorphisms, $$\begin{array}{lll} \star:C^k(K)\to C^{n-k}(K^\star ),& k=0,1, ...,n,\\ \star:C^k(K^\star)\to C^{n-k}(K),& k=0,1, ...,n, \end{array}$$ defined by $$\star (\psi) :=\psi^{\star}.$$

Proposition. The matrix of the Hodge star operator is diagonal with $$\star_{ii}=\tfrac{|a_i|}{|a^\star_i|}\cos\widehat{a a^\star},$$ where $a_i$ is the $i$th cell of $K$.

Exercise. Prove the proposition.

As before, we use in dimension $n=1$: $$\star ^1_{ii}=\frac{|\text{point}|}{|\text{edge}|} = \frac{1}{\text{length}} = \frac{1}{\Delta x}.$$ Computing Hodge duality of forms over a complex with a non-trivial geometry is only slightly more complicated than for the standard case:

Link to file: Spreadsheets.

In dimension $n=2$, we have the following diagonal entries for a rectangular grid: $$\begin{array}{llllll} \star ^2_{ii}&=\frac{|\text{point}|}{|\text{rectangle}|} &= \frac{1}{\text{area}} &=\frac{1}{\Delta x \Delta y},\\ \star ^1_{ii}&=\frac{|\text{edge}|}{|\text{edge}|} &= \frac{\text{length}}{\text{length}} &=\frac{\Delta y}{\Delta x}. \end{array}$$

In a $2$-dimensional cubical complex, combining two $1$-cells may produce different orientations and, therefore, different signs. Since $a \times d=\tau$ but $d \times a =-\tau$, the duality operator is $$\begin{array}{lll} \Big([0,1]\times \{0\}\Big)^\star &=\{0\}\times [0,1],\\ \Big(\{0\}\times [0,1]\Big)^\star &= -[0,1]\times \{0\}. \end{array}$$ In general, we are guided by the following rule.

Sign convention: The sign of the Hodge star is determined by: $$\star \star \alpha = (-1)^{k(n-k)} \alpha,$$ for a $k$-form $\alpha$.

Exercise. Confirm the sign convention for ${\mathbb R}^n$.

The Laplace operator

Let's review what we know about the derivatives.

Given a function $f$, we know that $ddf=0$. Therefore, the “second exterior derivative” is always trivial. Instead, one can define the “Hodge-dualized” second derivative computed following these four steps:

• find the exterior derivative $df$ of,
• “dualize” $df$,
• find the exterior derivative of the result, and then
• “dualize” the outcome back.

We can write the formula explicitly for ${\mathbb R}$: $$f \stackrel{d}{\longmapsto} df = f' dx \stackrel{\star}{\longmapsto} f' \stackrel{d}{\longmapsto} f' ' dx \stackrel{\star}{\longmapsto} f' '.$$ Then, for a $0$-form, this is, again, a $0$-form. This computation relies on a new, dual grid. In it, the new vertices are the centers of each $1$-cell. We assign the values of $df$ to these new vertices and then evaluate the exterior derivative of the result. Note that no derivative is defined at the endpoints of a $1$-dimensional complex.

Thus, given two values assigned to two adjacent cells, one assigns their difference to the cell in-between, illustrated below with a spreadsheet:

Suppose now a metric complex $K$ of an arbitrary dimension $n$ is given. Consider its Hodge duality diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccccccccc} 0& \ra{d} &C^0(K)& \ra{d} & C^1(K) &\ra{d} &... &\ \ra{d}& C^{n-1}(K)\ & \ra{d} & C^n(K)\ & \ra{d} & 0\\ \ \da{0} & \ne &\da{\star}\ua{} & \ne & \da{\star}\ua{} & & & &\da{\star}\ua{} & \ne & \da{\star}\ua{} & \ne &\ \da{0} \\ 0& \la{d} &C^n(K^\star)\ & \la{d} & C^{n-1}(K^\star)\ & \la{d}&... &\ \la{d}& C^1(K^\star)& \la{d} & C^0 & \la{d} & 0\\ \end{array} $$ Then, the generalizations of both first and second derivatives of $0$-forms are straight-forward and visible in the diagram.

Definition. The second derivative of a $0$-form $f$ is defined to be $$f ' ':=\star d \star df.$$

We recognize $f' '$ as the result of going around the leftmost square starting from the top left.

But what about higher order forms? What is the second derivative of $\varphi \in C^n$? We can still consider $\star d \star d \varphi$ but, as we follow the square on the right, the value is zero!

We notice that this time there is another square adjacent to $C^n$, on the left. Then we can, alternatively, first take the Hodge dual, then the exterior derivative, and continue around that square. The result is another “Hodge-dualized” second derivative.

Definition. The second derivative of an $n$-form $\varphi$ is defined to be $$\varphi' ':=d \star d \star \varphi.$$

We will use the same notation when there is no confusion. Both are implicitly present in the following: $$(\varphi' ')^\star = \star(d \star d \star \varphi)=(\star d \star d \star ) \varphi= (\varphi^\star)' '.$$

As we move to the general $k$-forms, we discover that, for $0<k<n$, there are two squares to follow and two, possibly non-trivial, second derivatives to be defined! Starting with a $k$-form, taking either of the two routes results in a new $k$-form: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccccc} & & C^{k-1} & \ra{d} & C^k & \ra{d} & C^{k+1} & \\ & & \ua{\star} & \ne & \da{\star} \ua{\star} & \ne & \da{\star} & \\ & & C^{n-(k-1)}& \la{d} & C^{n-k}& \la{d} & C^{n-(k+1)} & \\ \end{array} $$ Neither of the two but rather their sum is the true substitute for the second derivative.

Definition. The Laplace operator of a metric complex $K$ is the operator $$\Delta: C^k(K)\to C^k(K),\ k=0,1, ...,$$ defined to be $$\Delta =\star d \star d + d \star d \star .$$

Proposition. The Laplace operator is a cochain map on $K$.

Exercise. (a) Prove the proposition. (b) Are $\star d$, $d \star$, $\star d \star d$, $d \star d \star$ also cochain maps? (c) Is the Laplace operator generated by a cell map?

Exercise. Compute the cohomology map of the Laplace operator for (a) $K={\mathbb R}^1$, (b) $K={\mathbb S}^1$, with the standard geometry.