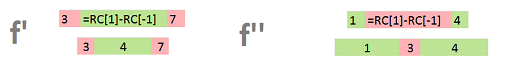Second derivative and the Laplacian

Redirect to:

• Geometry#The Laplace operator

Given a function $f$, we know that $ddf=0$. So the "second exterior derivative" is always trivial. Instead, one can define the "dualized" second exterior derivative as follows:

• "dualize" the exterior derivative $df$,
• take the exterior derivative of the result, and then
• "dualize" it back:

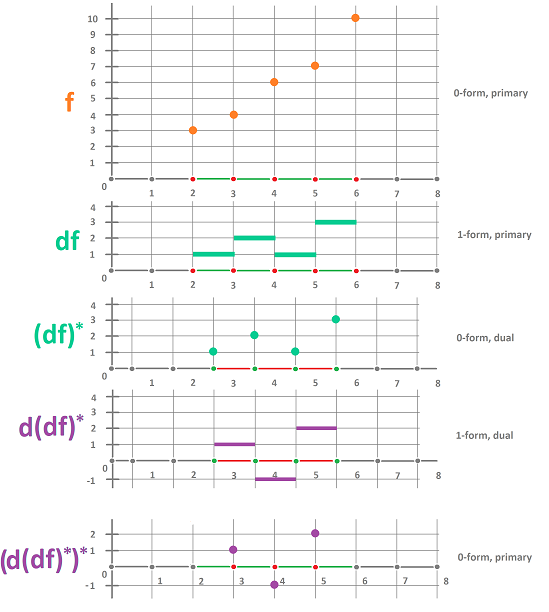
$$f \stackrel{d}{\longmapsto} df = f' dx \stackrel{\star}{\longmapsto} f' \stackrel{d}{\longmapsto} f' ' dx \stackrel{\star}{\longmapsto} f' '.$$ So, for a $0$-form this is, again, a $0$-form.

What is $\star df$ in the discrete case?

We need a new grid, called the dual grid. In it, the new vertices are the centers of each $1$-cell:

Then we assign the values of $df$ to these new vertices. As you can see we can now evaluate the exterior derivative of the result.

Note: no derivative defined at the end-points.

The logic is similar to the one we used to develop the discrete exterior derivative: given two values assigned to two adjacent cells, on assigns their difference to the cell in between. It is illustrated below with Excel:

Consider this Hodge duality diagram, where $\star$ stands for Hodge duality of differential forms: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} &C^{0}& \ra{d} & C^1 &\ra{d} &... & \ra{d}& C^k & \ra{d} & C^{k+1} & \ra{d} &...& \ra{d} & C^{n}\\ &\da{\star} & \ne & \da{\star} & & & & \da{\star} & \ne & \da{\star} & & & & \da{\star} \\ &C^{n}& \la{d} & C^{n-1}& \la{d}&... & \la{d}& C^{n-k}& \la{d}& C^{n-(k+1)}& \la{d} &...& \la{d} & C^{0} \\ \end{array} $$ Then the second derivative above is the result of going around the leftmost square.

Of course, we have the identical diagram for continuous forms where $C^k$ is replaced with $\Omega^k$, another cochain complex.

For a $k$-form, we consider $$\star d \star d \varphi.$$ We just make a full circle around one of the squares in the duality diagram, starting with $C^k$: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} & & C^{k-1} & \ra{d} & C^k & \ra{d} & C^{k+1} & \\ & & \da{\star} & \ne & \da{\star} & \ne & \da{\star} & \\ & & C^{n-(k-1)}& \la{d} & C^{n-k}& \la{d} & C^{n-(k+1)} & \\ \end{array} $$ Alternatively, we can first take Hodge dual and then exterior derivative and continue around the adjacent square. The result is another "dualized second derivative" of a $k$-form $$d \star d \star \varphi.$$ Either formula produces another a $k$-form.

The Laplace-de Rham operator is the analogue of the usual Laplacian $\Delta$ for differential forms. It is defined as the sum of the two "derivatives" above: $$\Delta \varphi =\star d \star d \varphi + d \star d \star \varphi.$$

Expressed in terms of the codifferential: $$\Delta=(\delta+d)^2 = \delta d + d\delta.$$ The notation could be also $\nabla ^2$.

In the $1$-dimensional case one of the terms disappears.

In the discrete $1$-dimensional case we are dealing with discrete differential forms of order $0$ and $1$. So the formula applies to a directed graph. In that case, the matrix $L$ of $\Delta$ can be computed directly: for each pair of vertices $u,v$,

• $L_{uv}=-1$ if $u,v$ are adjacent,
• $L_{uu}=d_u$, the degree of $u$,
• $L_{uv}=0$ if $u,v$ are not adjacent or equal.

Exercise. Prove the formula.