This site is being phased out.
Classification of points with respect to a subset
Redirect to:
For the background see Introduction to point-set topology.
Given a set $A$ in $X$,
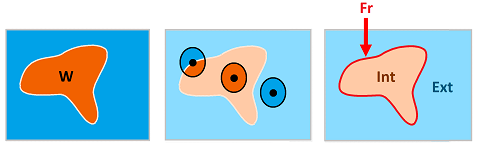
- a point $x$ is called an interior point of $A$ if there is a neighborhood $W$ of $x$ that lies entirely in $A$.
In other words, $x$ is isolated from the complement of $A$ by a neighborhood.
Then an open set $U$ coincides with the set of its interior points, called the interior ${\rm \hspace{3pt} Int}(U)$. In fact,
Theorem. ${\rm \hspace{3pt} Int}(A)$ is open for any $A$.
Example. The interior points of $A = [0,1]$ in ${\bf R}$ are $(0,1)$. Same for $(0,1], [0,1)$, and $(0,1)$.
In ${\bf R}^2$, if
Also, $${\rm Int}(D) = D.$$
Example. The interior of a circle $C = \{(x,y): x^2 + y^2 = 1 \}$ is empty.
Now, a point $x$ is called an exterior point of $A$ if there is a neighborhood $W$ of $x$ that lies entirely in $X \setminus A$.
In other words, exterior points are interior points of the complement.
Example. in ${\bf R}$, suppose $P$ is the set of point of the sequence $\{ \frac{1}{n}: n=1,2... \}$. Then the exterior points of $P$ are all points in the complement of $P$ except for $0$. Why not $0$? Because $\frac{1}{n}$ converges to $0$: for any $\epsilon >0$ there is a large enough $n$ so that $\frac{1}{n} \in B(0, \epsilon)$. ${\rm Int}(P)$ is empty.
Next, a point $x$ is called a limit point of $x$ if for any neighborhood $W$ of $x$ $$W \cap A \neq \emptyset.$$
Certainly, $0$ is a limit point for the set $P$ above. But also note that any point $x$ in $A$ is a limit point of $A$ since $x \in W \cap A$.
A point $x$ in $A$ is called isolated if there is a neighborhood $W$ of $x$ that the intersection of which with $A$ is $\{x \}$.
Example. Suppose $Q$ is the set of point of the sequence $\{ \frac{1}{n}: n = 1,2... \}$ combined with the limit, $0$. Then all points of $Q$ are isolated except for $0$. Why? Once again, because $\frac{1}{n} \rightarrow 0$.
A point $x$ is called a frontier point of $A$ if it is a limit point for both the set $A$ and its complement.
The condition can be restated as: any neighborhood $W$ of $x$ intersects both $A$ and $X \setminus A$.
Example. The set of all frontier points, its frontier ${\rm \hspace{3pt} Fr}(D)$, of the open disk $A$ is the circle $C$.
Definition. The closure, ${\rm \hspace{3pt} Cl}(A)$, of $A$ is the set of all limit points of $A$.
The following two theorems are obvious.
Theorem. $${\rm Int}(A) \subset A \subset {\rm \hspace{3pt} Cl}(A).$$
Theorem. $${\rm Cl}(A) = {\rm \hspace{3pt} Int}(A) \cup {\rm \hspace{3pt} Fr}(A).$$
Theorem.
- ${\rm Int}(A)$ is open.
- ${\rm Fr}(A)$ is closed.
- ${\rm Cl}(A)$ is closed.
Proof. (1) is obvious. (2) and (3) exercise below. $\blacksquare$
Theorem. For any set $A$ in $X$, the interior, the frontier, and the exterior of $A$, i.e.,
To summarize these definitions...
Consider the missing parts in the sentence:
- "If there is a neighborhood $W$ of $x$ in $A$ so that ......., then $x$ is a ....... point."
We can complete this as follows:
- .............................................................. $W \subset A$ .................................. interior ........
or
- .............................................................. $W \subset X \setminus A$ .............................. exterior ........
Consider another sentence:
- "If for any neighborhood $W$ of $x$ in $A$ we have ......., then $x$ is a ....... point."
We can complete this as follows:
- ............................................................... $W \cap A \neq \emptyset$ .............................. limit ..........
or
- ............................................................... $W \cap A \neq \emptyset$ and $W \cap (X \setminus A) \neq \emptyset$ .......... frontier ........
For more examples see Realizations of cubical complexes.
Exercise.
- (1) Prove that the closure of $A$ is the intersection of a certain collection of closed sets. =>
- (2) Prove that the closure is closed. =>
- (3) Prove that the frontier is closed. Solution:
