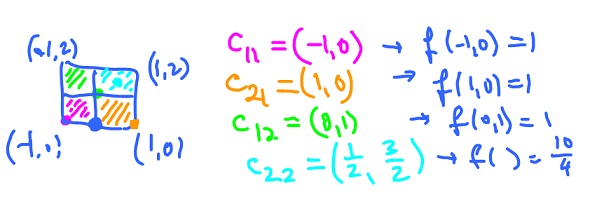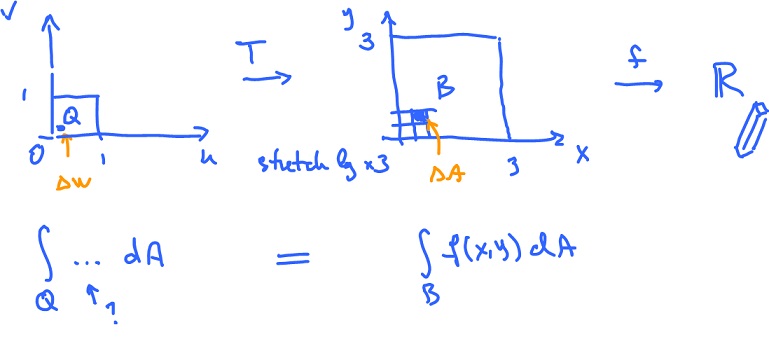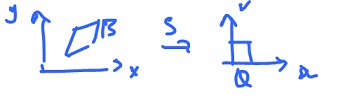Integration in dimension n

Introduction

We want to learn to compute:

lengths, areas, and volumes.

Plus whatever is the analogue of volume in dimension $n$. To be consistent we use the word "volume" for all dimensions:

• $1$-volume = length,
• $2$-volume = area,
• $3$-volume = volume, etc.

We start with the elementary parts for every dimension:

${\bf R}$: ($1$-dimensional volume). Lengths of intervals

$$l[u,v] = v - u.$$

This helps with all other dimensions.

${\bf R}^2$: The area of a rectangle with sides $a$ and $b$ is

$$A = a \cdot b.$$

You also find the areas of triangles ($2$-volume) as halves of rectangles. (How do you compute/define the area of a circle though?)

${\bf R}^3$: The volume of a box with sides $a$, $b$ and $c$ is

$$V = a \cdot b \cdot c.$$

${\bf R}^n$: Definition. The $n$-volume of the $n$-dimensional "box" $B$ with lengths of its sides equal to $a_1, ..., a_n$ is

$$\displaystyle\prod_{i=1}^n a_i.$$

Here the box is given by

$$\begin{array}{} B &= \{ x \in {\bf R}^n: p_i ≤ x_i ≤ q_i, i = 1, ..., n \}, p_i < q_i \\ &= [ p_1, q_1 ] \times \ldots \times [ p_n, q_n ]. \end{array}$$

(see Products of sets)

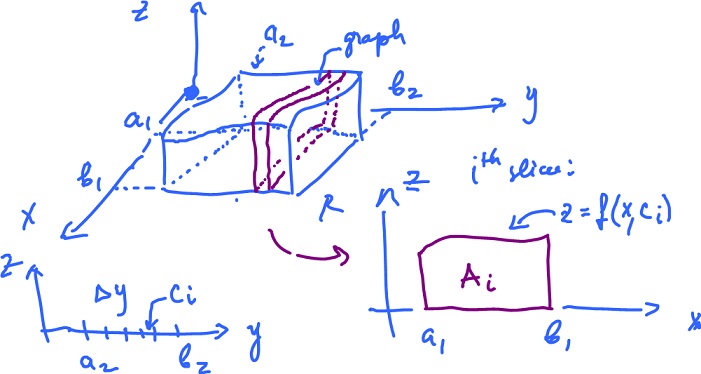
Review of Riemann integral

We start Calc 1. This means that we deal with

$f: [ a, b ] \rightarrow {\bf R}$ continuous

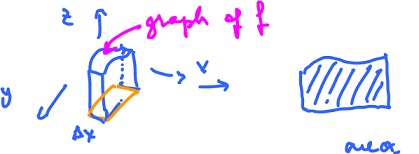
and its graph lies in ${\bf R}^2$. Riemann integral defines "the area under the graph of $f$".

Note: This makes sense in dimension $3$ - volume under the surface and in dimension $n$:

let $f: n$-dim box $\rightarrow {\bf R}$ be scalar function, then

$${\rm graph \hspace{3pt}} f \subset {\bf R}^{n+1}.$$

Then it makes sense to talk about the $(n+1)$-dimensional volume "under the graph" of $f$.

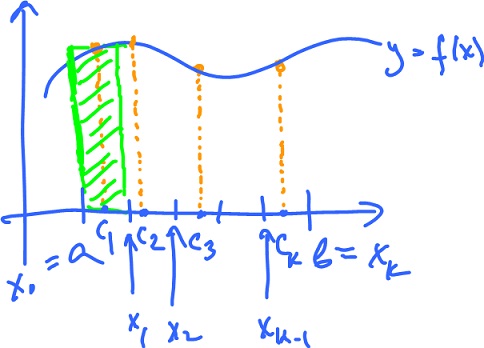
The idea is to approximate the area with rectangles.

1. Pick $k$, the number of intervals.
2. Cut $[a,b]$ into $k$ intervals of equal length: $$a = x_0 < x_1 < ... < x_k = l.$$
3. Pick a point in each: $c_1, ..., c_k$.
4. Evaluate $f$ at $c_1, ..., c_k$. These numbers are the heights of rectangles, while the bases are $[ x_i, x_{i+1}]$, the intervals.

Note: In dimension $n$, the $n$-dimensional box is divided into $n$-dimensional boxes, maybe via dividing each coordinate into $k$ intervals. This yields an $n$-dimensional grid.

Calculate the areas of the rectangles and add them up:

widths of rectangles ${\Delta}x = \frac{b - a}{k}$,
heights of rectangles $f( c_1 ), ..., f( c_k)$.

Then we get

total area of rectangles $= f(c_1) {\Delta}x + f(c_2) {\Delta}x + ... + f(c_k) {\Delta}x$,

called the Riemann sum of $f$ for this partition of $[ a, b ]$.

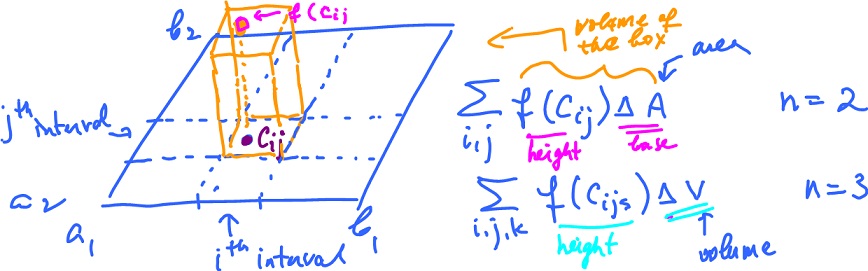
Note: In dimension $n$ we have

box $B = [ a_1, b_1 ] \times ... \times [ a_n, b_n ]$.

This is the product of $n$ intervals. Then each of those is sub-divided into $k$ intervals. Then the volume is the sum of the volumes of the boxes, in total there are $k^n$. Integrate over $B$ to get the $( n + 1 )$-dimensional volume.

For more see Riemann integral.

Volumes and integrals

We consider

$$f: {\bf R}^n → {\bf R}.$$

The volume of the box

$$B = \displaystyle\prod_{i=1}^n [ a_i, b_i ]$$

is

$$V = \displaystyle\prod_{i=1}^n ( b_i - a_i ),$$

i.e. the volume of the product of $n$ intervals is the product of their lengths.

In ${\rm dim \hspace{3pt}} = 2$, the area is

$${\Delta}A = ( b_1 - a_1 ) \cdot ( b_2 - a_2 ),$$

and in ${\rm dim \hspace{3pt}} = 3$, the volume is

$${\Delta}V = ( b_1 - a_1 ) \cdot ( b_2 - a_2 ) \cdot ( b_3 - a_3 ).$$

In general, the volume of each little box is

$${\Delta}V = \displaystyle\prod_{i=1}^n \frac{b_i - a_i}{k^n} \rightarrow 0 {\rm \hspace{3pt} as \hspace{3pt}} k \rightarrow \infty.$$

The Riemann sum of $f: B \rightarrow {\bf R}$ for this partition:

Each $[ a_i, b_i ]$ is divided into $k$ intervals, and each interval has a point in it, call it $c_{ii}$.

In ${\rm dim \hspace{3pt}} = 2$:

$\displaystyle\sum_{i,j} f( c_{ij} ) {\Delta}A$, where

the $3$-volume of each box is $f( c_{ij} ) {\Delta}A$, and
the height is $f( c_{ij} )$, and

the base is ${\Delta}A$.

In {\rm dim \hspace{3pt}} = 3$:

$\displaystyle\sum_{i,j,k} f( c_{ijk} ) {\Delta}V$, where

the $4$-volume of each box is $f( c_{ijk} ) {\Delta}V$, and
the height is $f( c_{ijk} )$,

and the $3$-volume (of the base) is ${\Delta}V$.

Back to ${\rm dim \hspace{3pt}} = 1$. Consider

$$\displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k f( c_i ) {\Delta}x$$

(or $\displaystyle\lim_{\Delta x \rightarrow 0}$ ...),

where $c_i$ denotes the midpoint of the respective intervals. If this limit exists, it is called the Riemann integral of $f$ from $a$ to $b$. We write

$$\displaystyle\int_a^b f(x) dx,$$

and call $f$ an integrable function on $[ a, b ]$.

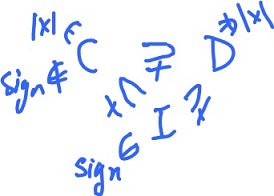
The relation of the sets of functions that are

• differentiable functions
• continuous functions
• integrable functions,

is shown on the right. The absolute value and the sign functions are the counterexamples.

For ${\rm dim \hspace{3pt}} = 2$ it's all very similar

$$\displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k f( c_{ij} ) {\Delta}A = \displaystyle\int\displaystyle\int_B f(x) dA,$$

where

$$B = [ a_1, b_1 ] \times [ a_2, b_2 ].$$

Example. Let's compute something. Let $f(x) = x, a = 0, b = 1$, and

$x_i = \frac{1}{k} i$ the endpoints for $i = 1, ..., k$ ($k$ intervals).
$c_i = \frac{1}{k}i$ chosen points for $i = 0, ..., k-1$.

Then

$$\begin{array}{} \displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k f( c_i ) {\Delta}x &= lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k c_i {\Delta}x \\ &= \displaystyle\lim_{k \rightarrow \infty} ( c_1 + ... + c_k ) \frac{1}{k} \\ &= \displaystyle\lim_{k \rightarrow \infty} ( 0 + \frac{1}{k} + \frac{2}{k} + ... + \frac{k - 1}{k} k \\ &= \displaystyle\lim_{k \rightarrow \infty} ( \frac{1}{k^2} + \frac{2}{k^2} + \ldots + \frac{k - 1}{k^2} ) {\rm \hspace{3pt} arithmetic \hspace{3pt} progression} \\ &= \frac{k \frac{k - 1}{2}}{k^2} \\ &= \frac{1}{2} \end{array}$$

So, $$\begin{array}{} \displaystyle\int_{[0,1]} x dx &= \displaystyle\int_0^1 x dx &= \frac{x^2}{2}|_0^1 &= \frac{1}{2}. \end{array}$$

Volume and mass

Q: Why do we need integrals?

A: Compute volumes of complicated figures and the mass of objects with non-uniform density.

We can certainly compute the volume of a box in any dimension but what about the ball, cylinder etc. Meanwhile the mass of even a simple figure isn't easy to compute unless it's made of uniform material.

Suppose we have a (real) box $B$ filled with stuff of varied density. Mathematically, the situation is captured by a function

$$d: B → {\bf R}^{+},$$

and $d( x, y, z )$ is the density at the point $( x, y, z )$.

What is the mass of $B$? Consider little cubes, each of volume ${\Delta}V$, then estimate the density of each cube by

$$d( e_i, d_j, e_l ), $$

where $( e_i, d_j, e_l )$ is a point in a cube. Then the estimated mass is

$$\displaystyle\sum_{i,j,l} d( e_i, d_j, e_l ) {\Delta}V,$$

which we recognize as a Riemann sum. It converges, as $k \rightarrow 0$, to

$$\displaystyle\int\displaystyle\int\displaystyle\int_B d( x, y, z) dV.$$

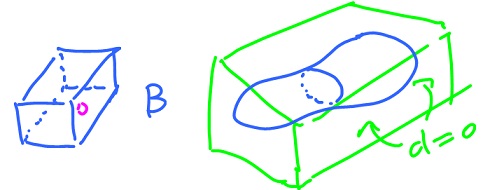
Note: we can compute the volume of a complex figure G by putting it in a box and setting the density equal to zero in the complement $B \setminus G$ of $G$.

Example. Let

$$R = [ 0, 1 ] \times [ 1, 2 ]. $$

Then what is

$$\displaystyle\int\displaystyle\int_R ( x^2 y ) dA?$$

We can reduce the above definite integral to indefinite integrals (i.e. antiderivatives), just like in Calc 1. Except now we have two variables of $x$ and $y$.

The idea is to cut the region into slices and compute the volume of each as a single integral, then add them.

Subdivide

$${\Delta}y = \frac{b_2 - a_2}{k}.$$

Suppose

the area of the $i$-th slice is $A_i$.

Then the volume equals the sum of the volumes of the slices, which is approximately

$$V \approx \displaystyle\sum_{i=1}^k A_i {\Delta}y$$

(i.e. the area of the cross section multiplied with the thickness). Find, by the Fundamental Theorem of Calculus,

$$\begin{array}{} A_i &= \displaystyle\int_{[a_1,b_1]} f( x_1, c_i ) dx \\ &= \displaystyle\int_{a_1}^{b_1} f( x_1, c_i ) dx, \end{array}$$

substitute:

$${\rm volume \hspace{3pt}} \approx \displaystyle\sum_{i=1}^k ( \displaystyle\int_{a_1}^{b_1} f( x_1, c_i ) dx ) {\Delta}y$$

$${\rm volume \hspace{3pt}} = \displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k [ \displaystyle\int_{a_1}^{b_1} f( x_1, c_i ) dx ] {\Delta}y.$$

The sum in the above formula is a Riemann sum with respect to $y$ on $[ a_2, b_2 ]$, but of what? Compare the above to

$$\displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k g( c_i ) {\Delta}y = \displaystyle\int_{a_2}^b2 g(y) dy.$$

What is $g$?

$$g(y) = \displaystyle\int_{a_1}^{b_1} f( x, y ) dx.$$

Further

$${\rm volume \hspace{3pt}} = \displaystyle\int_{a_2}^b2 \displaystyle\int_{a_1}^{b_1} f( x, y ) dx dy$$

These are definite integrals (dimension 1). They are computed by the FTC. For our specific function we have:

$$\begin{array}{} = \displaystyle\int_0^1 ( \displaystyle\int_0^1 x^2 y dx ) dy \\ = \displaystyle\int_0^1 ( \frac{1}{3} x^3 y |_{x=0}^{x=1} ) dy \\ = \displaystyle\int_0^1 ( \frac{1}{3} y - 0 ) dy \\ = \frac{y^2}{6} |_0^1 = \frac{1}{6}. \end{array}$$

For more see Mass as an integral and Volume as an integral.

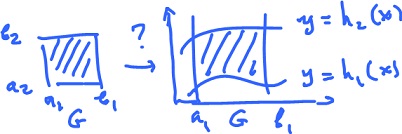
Integration with curved domains

What about more complex, curved domains? What if the domain of integration $G$ is represented as a "curvilinear" rectangle, bounded by the graphs of two functions?

What is then

$$\displaystyle\int\displaystyle\int_G f( x, y ) dA?$$

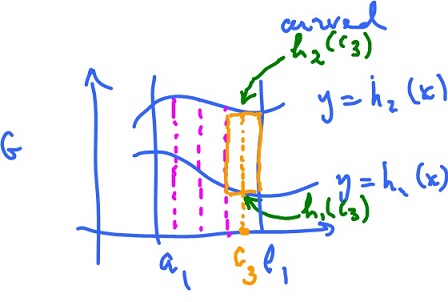
We just slightly generalize the construction. Subdivide $[a, b]$ into $x_0, x_1, ..., x_k,$ where

$$x_0 = a_1, x_k = b_1.$$

Choose $c_1, ..., c_k$ in each:

$$c_i \in [ x_i, x_{i+1} ].$$

The volume of the region above each rectangle, under the graph of $f$ is approximately

the area under the graph $\cdot$ the thickness of the slice, or

$$\displaystyle\int_{h_1(c_i)}^{h_2(c_i)} f( c_i, y ) dy \cdot {\Delta}x.$$

Take the sum of these, together they approximate the volume over the region $G$ below the graph of $f$:

volume $= \displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k \displaystyle\int_{h_1(c_i)}^{h_2(c_i)} f( c_i, y ) dy {\Delta}x.$

This is a Riemann sum, but of what? Of the integral inside:

$$g(x) = \displaystyle\int_{h_1(x)}^{h_2(x)} f( x, y ) dy.$$

Then

$volume = \displaystyle\int_{a_1}^{b_1} \displaystyle\int_{h_1(x)}^{h_2(x)} f( x, y ) dy dx.$

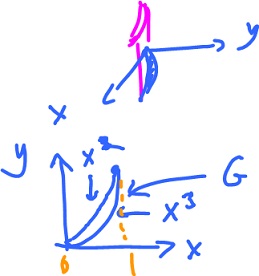
Example. Compute the volume in ${\bf R}^3$ of the region bounded by

$$y = x^2, y = x^3, xy-plane, z = x + y.$$

Solution: Find $a_1, b_1, h_1, h_2, f$,

$$z: f( x, y ) = x + y,$$

$$y: h_1(x) = x^3, h_2(x) = x^2$$

$$x: a_1 = 0, b_1 = 1.$$

Then by the formula:

$$\begin{array}{} V &= \displaystyle\int\displaystyle\int_G ( x + y ) dA \\ &= \displaystyle\int_0^1 ( \displaystyle\int_{y=x^3}^{y=x^2} ( x + y ) dy ) dx \\ &= \displaystyle\int_0^1 ( xy + \frac{1}{2} y^2 |_{y=x^3}^{y=x^2} ) dx \\ &= \displaystyle\int_0^1 ( x^3 + \frac{1}{2} x^4 - x^4 - \frac{1}{2} x^6 ) dx \\ &= \frac{x^4}{4} - \frac{x^5}{10} - \frac{x^7}{14} |_0^1 \\ &= \frac{1}{4} - \frac{1}{10} - \frac{1}{14} ( > 0 ) \end{array}$$

Integration examples

Example. (a) Give a Riemann sum with $k = 2, 4$ rectangles, for

$$\displaystyle\int\displaystyle\int_B ( x^2 + y^2 ) dA, $$

and the rectangle on the right. Let

$$f_n = ( x^2 + y^2 ).$$

For each rectangle $(1 \times 1)$, ${\Delta}A = 1$, and the Riemann sum is

$$\displaystyle\sum_{i,j=1}^k f( c_{ij} ) {\Delta}A$$

with $c_{ij}$ in $R_{ij}$. Then we obtain

$$c_{11} = ( -1, 0 ) \rightarrow f( -1, 0 ) = 1,$$

$$c_{21} = ( 1, 0 ) \rightarrow f( 1, 0 ) = 1,$$

$$c_{12} = ( 0, 1 ) \rightarrow f( 0, 1 ) = 1,$$

$$c_{22} = ( \frac{1}{2}, \frac{3}{2} ) \rightarrow f( \frac{1}{2}, \frac{3}{2} ) = \frac{10}{4}.$$ Then the Riemann sum is

$$1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 + \frac{10}{4} \cdot 1 = 5 \frac{1}{2}.$$

Exercise. Above we chose $c_{ij}$ randomly, but what if we want to maximize $f$ on each $R_{ij}$?

Consider the the Riemann sum:

$$f( -1, 1 ) + f( 1, 1 ) + f( -1, 2 ) + f( 1, 2 ) = 2 + 2 + 5 + 5 = 14$$

Then

$$\displaystyle\int_B f( x, y ) dA \leq 14.$$

What about the lower bound for the integral?

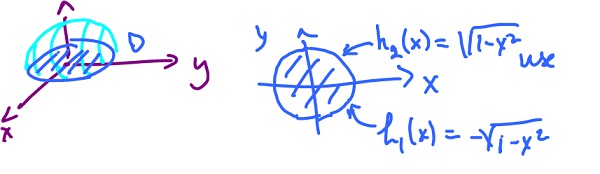
Example. Calculate

$$I = \displaystyle\int_D ( 1 - x^2 - y^2 )^{\frac{1}{2}} dA,$$

where

$$D = \{ ( x, y ): x^2 + y^2 \leq 1 \}.$$

Then

$z = ( 1 - x^2 - y^2 )^{\frac{1}{2}} \rightarrow x^2 + y^2 + z^2 = 1,$ sphere.

Use iterated integration. Then

$$I = \displaystyle\int_{-1}^1 \displaystyle\int_{\sqrt{1-x^2}}^{\sqrt{1-x^2}} ( 1 - x^2 - y^2 )^{\frac{1}{2}} dy dx.$$

To evaluate

$$\displaystyle\int ( 1 - x^2 - y^2 )^{\frac{1}{2}} dy$$

we need trigonometric substitution. This means we have to carry out separate trigonometric substitution for each $x$. Instead we do trigonometric" substitution for $( x, y )$ which turns into the "change of variables" and the new variable are the polar coordinates:

$$( x, y ) \rightarrow ( r, θ )$$

$$x = r {\rm \hspace{3pt} cos \hspace{3pt}} \theta {\longleftrightarrow} r = ( x^2 - y^2 )^{\frac{1}{2}}$$

$$y = r {\rm \hspace{3pt} sin \hspace{3pt}} \theta {\longleftrightarrow} \theta = {\rm arctan \hspace{3pt}} \frac{y}{x}.$$

Also Area integral: examples.

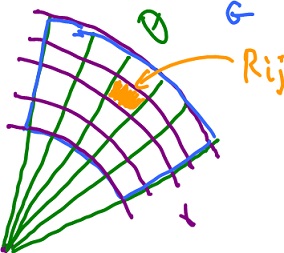
Riemann integral for polar coordinates

We want to utilize the geometry of polar coordinate system to make integration over some (curved) regions simpler.

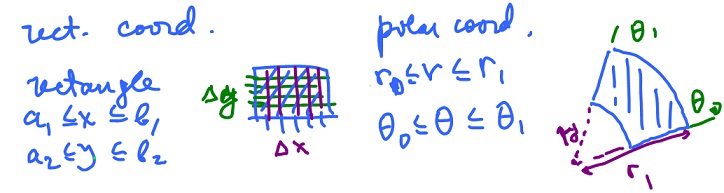
Let' start with $2D$ Cartesian coordinates. We integrate over a rectangle:

$$a_1 \leq x \leq b_1, a_2 \leq y \leq b_2.$$

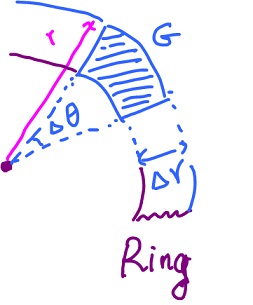
Now, we follow the same procedure with polar coordinates:

$$r_0 \leq r \leq r_1, \theta_0 \leq \theta \leq \theta_1$$

The geometry of this "rectangle" is different of course. In fact, we have

a circle: $0 \leq r \leq 1, 0 \leq \theta \leq 2{\pi}.$

To compute

$$\displaystyle\int\displaystyle\int_G f( x, y ) dA $$

in polar coordinates (volume under the graph) we need some kind of Riemann sum. What we do exactly mimics the rectangular case, but only algebraically:

1. divide $[ \theta_0, \theta_1 ]$ into $k$ intervals,
2. length ${\Delta} \theta$,
3. divide $[ r_0, r_1 ]$ into $k$ intervals,
4. length ${\Delta}r$,
5. evaluate $f( r_i, \theta_j )$ with each $( r_i, \theta_j )$ in $R_{ij}$.

Then the Riemann sum is

$$\displaystyle\sum_{i=1}^k \displaystyle\sum_{j=1}^k f( r_i, θ_j ) {\Delta}A,$$

where ${\Delta}A$ is the area of the rectangle $R_{ij}$.

Approximate the volume by the sum of these volumes,

volume $=$ height $\cdot$ area of the base

We compute the area of the curved rectangle with sides ${\Delta}r, {\Delta} \theta$, which varies with the location (unlike rectangular). How? Consider a circle with radius $r$ and area ${\pi}r^2$, and another circle with radius $r - {\Delta}r$ and area ${\pi}( r - {\Delta}r )^2$. Then we obtain a ring with area

$$\begin{array}{} {\pi}r^2 - {\pi}( r - {\Delta}r )^2 &= {\pi}( r^2 - ( r - {\Delta}r )^2 ) \\ &= {\pi}( 2r - {\Delta}r ) {\Delta}r \\ &= ( r - \frac{{\Delta}r}{2} ) {\Delta}r {\Delta}θ. \end{array}$$

"Rectangle", $R$, the area is equal the the area of a ring multiplied by $\frac{{\Delta} \theta}{2{\pi}}$, hence

area $= \frac{1}{2} ( 2r - {\Delta}r ) {\Delta}r {\Delta} \theta, \theta_i \leq \theta \leq \theta_i + {\Delta} \theta$.

The total volume is approximated by the Riemann sum

$$\begin{array}{} \displaystyle\sum_{i,j}^k f( r_i, \theta_j ) ( r - \frac{{\Delta}r}{2} ) {\Delta}r {\Delta} \theta &= \ldots \\ &= \displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i,j}^k f( r_i, \theta_j ) ( r - \frac{{\Delta}r}{2} ) {\Delta}r {\Delta} \theta \\ &= \displaystyle\int_{\theta_0}^{\theta _1} \displaystyle\int_{r_0}^{r_1} f( r, \theta ) r dr d \theta. \end{array}$$

Example. Compute the volume of the half-sphere

$$\displaystyle\int\displaystyle\int_D ( 1 - x^2 - y^2 )^{\frac{1}{2}} dA$$

with $D: 0 \leq \theta \leq 2{\pi}, 0 \leq r \leq 1$. Further

$$g( x, y ) \rightarrow f( r, θ ),$$

$$z = ( 1 - x^2 - y^2 )^{\frac{1}{2}} \rightarrow ( 1 - ( r {\rm \hspace{3pt} cos \hspace{3pt}} \theta )^2 - ( {\rm \hspace{3pt} sin \hspace{3pt}} \theta )^2 )^{\frac{1}{2}} = ( 1 - r^2 )^{\frac{1}{2}}.$$

Then

$$\begin{array}{} V &= \displaystyle\int_{\theta = 0}^{\theta = 2 \pi} \displaystyle\int_{r=0}^{r=1} ( 1 - r^2 )^{\frac{1}{2}} r d \theta dr \\ &= 2{\pi} \displaystyle\int_0^1 ( 1 - r^2 )^{\frac{1}{2}} r dr. \end{array}$$

Finally, with

$$u = 1 - r^2 , du = -2 r dr$$

we have

$$\begin{array}{} 2{\pi} \displaystyle\int_0^1 u^{\frac{1}{2}} ( -\frac{1}{2} ) du &= \frac{2{\pi}}{2} \cdot \frac{2}{3} \cdot u^{\frac{3}{2}} |_0^1 \\ &= \frac{2}{3} \cdot {\pi}. \end{array}$$

Example. Compute the area of a circle:

$A =$ the volume under the graph of $f( x, y ) = 1$.

$$\begin{array}{} A &= V = \displaystyle\int\displaystyle\int_D 1 dA \\ &= \displaystyle\int_0^{2 \pi} \displaystyle\int_0^1 r dr d \theta \\ &= \displaystyle\int_0^{2 \pi} \frac{r^2}{2} |_0^1 d \theta \\ &= \displaystyle\int_0^{2 \pi} \frac{1}{2} d \theta \\ &= 2{\pi} \cdot \frac{1}{2} \\ &= {\pi}. \end{array}$$

Note that in

$$\displaystyle\int_Q g( x, y ) dA = \displaystyle\int_R g( r {\rm \hspace{3pt} cos \hspace{3pt}} \theta, r {\rm \hspace{3pt} sin \hspace{3pt}} \theta ) r dr d \theta,$$

$g( r {\rm \hspace{3pt} cos \hspace{3pt}} \theta, r {\rm \hspace{3pt} sin \hspace{3pt}} \theta ) r$ is a composition.

Properties of the integral

Iterated integral formula: $\displaystyle\int\int_Q \ldots dA = \displaystyle\int_a^b \displaystyle\int_c^d \ldots dx dy$

We will derive some of the general properties of Riemann integral in dimension $n$. They certainly can be derived from the iterated integral formula which allow us to invoke the properties of the integral in dimension $1$. Instead we will do that based on the definition of the Riemann sum if it exists.

Let ${\rm dim \hspace{3pt}} = n$ and $f: {\bf R}^n \rightarrow {\bf R}$.

$$\displaystyle\int_Q f(n) dV = \displaystyle\lim_{m \rightarrow \infty} \displaystyle\sum_i f( e_i ) {\Delta}V,$$

a (n+1)-dimensional volume where ${\Delta}V$ an $n$-dimensional volume of an $n$-dimensional box. Altogether we have $m^n$ boxes.

In the $2$ dim case, if

• $Q$ is a rectangle, or
• $Q$ is a union of several rectangles, or
• $Q$ is bounded by two surfaces (h_1(u) ≤ z ≤ h_2(u), u ∈ {\bf R}^n),

and

$- f$ is continuous,

then

$\displaystyle\int_Q f(x,y) dA$ exists

(i.e. the limit exists). However, the properties below apply to the $n$ dim case:

$$\displaystyle\int_Q f(u) dV.$$

Property $1$ (Sum rule of integral). Integration preserves addition.

Let $f, g$ continuous. Then

$$\begin{array}{} \displaystyle\int_Q ( f(u) + g(u) ) dV &= \displaystyle\lim_{i \rightarrow \infty} \displaystyle\sum_i ( f(c_i) + g(c_i) ) {\Delta}V \\ &= \displaystyle\lim_{i \rightarrow \infty} ( \displaystyle\sum_i f(c_i) {\Delta}V + \displaystyle\sum_i g(c_i) {\Delta}V ) \\ &= \displaystyle\lim_{i \rightarrow \infty} \displaystyle\sum_i f(c_i) {\Delta}V + \displaystyle\lim_{i \rightarrow \infty}\displaystyle\sum_i g(c_i) {\Delta}V {\rm \hspace{3pt} (sum \hspace{3pt} rule \hspace{3pt} of \hspace{3pt} limits)} \\ &= \displaystyle\int_Q f(u) dV + \displaystyle\int_Q g(u) dV. \end{array}$$

Note: Even though this property is about addition, there is another additivity property below.

Property 2 (Additivity of integral). Integration is additive with respect to the union of domains of integration.

Suppose $Q, R$, with $Q {\cap} R = \emptyset$. Then

$$\displaystyle\int_{Q \cup R} f(u) dV = \displaystyle\int_Q f(u) dV + \displaystyle\int_R f(u) dV$$

What if $Q {\cap} R {\neq} \emptyset$? In this case,

$$\displaystyle\int_{Q \cup R} f(u) dV = \displaystyle\int_Q f(u) dV + \displaystyle\int_R f(u) dV - \displaystyle\int_{Q \cap R} f(u) dV.$$

Property 3 (Homogeneity of integral). Integration preserves scalar multiplication.

$$\begin{array}{} \displaystyle\int_Q k f(u) dV = \displaystyle\lim_{m \rightarrow \infty} \displaystyle\sum_i k f(c_i) {\Delta}V \\ &= k \displaystyle\lim_{m \rightarrow \infty} \displaystyle\sum_i f(c_i) {\Delta}V \\ &= k \displaystyle\int_Q f(u) dV \end{array}$$

Property 4 (Positivity of integral). The integral of a positive function is positive.

If $f(u) \geq 0$ for all $u \in Q$, then $\displaystyle\int_Q f(u) dV \geq 0$.

(Since $f(c_i) \geq 0, {\Delta}V \geq 0$ in Riemann sums)

It follows then,

if $f(u) \geq g(u)$ for all $u \in Q$, then $\displaystyle\int_Q f(u) dV \geq \displaystyle\int_Q g(u) dV$.

Property 5 (Normalization of integral). The integral of $1$ is equal to the area of the domain of integration.

$$\begin{array}{} \displaystyle\int_Q 1 dV &= n{\rm -dimensional \hspace{3pt} volume\hspace{3pt} of \hspace{3pt}} Q, {\rm \hspace{3pt} where \hspace{3pt}} Q \subset {\bf R}^n \\ &= \displaystyle\lim_{m \rightarrow \infty} \displaystyle\sum_i 1 {\Delta}V {\rm \hspace{3pt} (Riemann \hspace{3pt} sum)} \\ &= \displaystyle\lim_{m \rightarrow \infty} \displaystyle\sum_i {\Delta}V, {\rm \hspace{3pt} where \hspace{3pt}} V {\rm \hspace{3pt} are \hspace{3pt} boxes \hspace{3pt} that \hspace{3pt} add \hspace{3pt} to \hspace{3pt} the \hspace{3pt} whole \hspace{3pt}} Q \\ &= \displaystyle\lim Q = Q. \end{array}$$

Properties $1$ and $3$ suggest that the integral is a linear operator in some sense?

Fix $Q \subset {\bf R}^n$, the region of integration, then $\displaystyle\int_Q f(u) dV = H(f) \in {\bf R}$, so that

$H: C(Q ) \rightarrow {\bf R}$ is a function,

$C( Q )$ is the set of all continuous functions $f: Q \rightarrow {\bf R}$, which is a vector space (of infinite dimension).

In this sense $H$ is a linear operator.

Property 6 (Integration with parameter). The integral of the derivative is the derivative of the integral.

Suppose $f: {\bf R}^2 \rightarrow {\bf R}$ is continuous on $Q = {\bf R} \times [ r, d ]$, and $\frac{\partial f}{\partial x}$ is continuous on $Q$. Then

$$\varphi(x) = \displaystyle\int_c^d f( x, y ) dy$$

is differentiable on ${\bf R} \times ( r, d )$ and

$$\varphi'(x) = \displaystyle\int_c^d \frac{\partial f}{\partial x} ( x, y ) dy,$$

Note 1: $x$ is the "parameter" here.

Note 2: also

$$\varphi'(x) = \left( \displaystyle\int_c^d f( x, y ) dy \right)'.$$

Exercise. Let

$$f( x, y ) = x^2 y^3, ({\rm try \hspace{3pt} also \hspace{3pt}} f( x, y ) = x^y). $$

Then

$$\begin{array}{} \varphi(x) &= \displaystyle\int_0^1 f( x, y ) dy \\ &= \ldots {\rm \hspace{3pt} explain \hspace{3pt} here} \\ \varphi'(x) &= \displaystyle\int_0^1 f'( x, y ) dy \\ &= \displaystyle\int_0^1 2x y^3 dy \\ &= 2x \frac{y^4}{4} |_0^1 \\ &= \frac{x}{2}. \end{array}$$

Change of variables in integral

Integration with respect to polar coordinates is just one example how one can an alternative coordinate system can make integration easier or even trivial.

We start with a simple example of alternative Cartesian system.

Let ${\rm \hspace{3pt} dim \hspace{3pt}} = 2$. Compute the integral

$$\displaystyle\int_B f( x, y ) dA$$

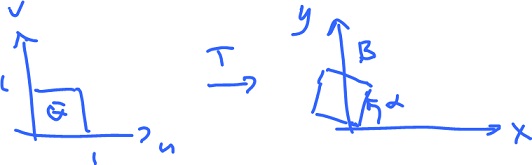
with respect to another coordinate system $( u, v )$. This system comes from a transformation

$$( x, y ) = T( u, v )$$

with $T: {\bf R}^2 \rightarrow {\bf R}^2$.

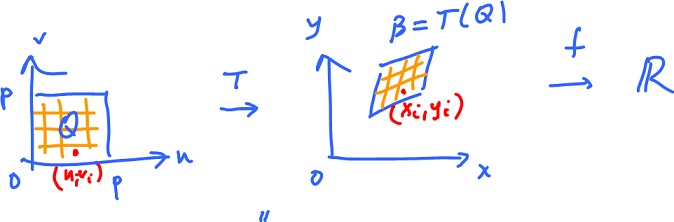
The question is: what is the function (of $u,v$) we should integrate over $Q$ to get the same result as integration of $f(x,y)$ over $B = T(Q)$:

$$\displaystyle\int_Q ... dA = \displaystyle\int_B f( x, y ) dA?$$

Compare the Riemann sums:

$$\displaystyle\sum_i f( T( u_i, v_i ) ) {\Delta}W =^{!!} \displaystyle\sum_i f( x_i, y_i ) {\Delta}A,$$

where the $u_i$ are the heights, ${\Delta}W$ the areas, the $x_i$ the heights and ${\Delta}A$ the area of the base. Then what is the correspondence:

$$T( u_i, v_i ) {\longleftrightarrow}^? ( x_i, y_i )$$

This is what we do know:

$$9 {\Delta}W {\longleftrightarrow} {\Delta}A$$

Then

$$\displaystyle\sum_i f( T( u_i, v_i ) ) 9 {\Delta}W = \displaystyle\sum_i f( x_i, y_i ) {\Delta}A,$$

where $( 9 {\Delta}W )$ equals ${\Delta}A$. Substitution and the limit and the Riemann sum of $f$, respectively, yield

$$\displaystyle\int_Q f( T( u, v )) 9 dW = \displaystyle\int_B f( x, y ) dA.$$

Where does this $9$ come from?

$$T( u, v ) = \left| \begin{array}{} 3 & 0 \\ 0 & 3 \end{array} \right| \left| \begin{array}{} 4 \\ v \end{array} \right|$$

and

$$T' = \left| \begin{array}{} 3 & 0 \\ 0 & 3 \end{array} \right|$$

Then $9 = | {\rm det \hspace{3pt}} T' |$. This is the "stretching coefficient".

Let's consider $| {\rm det \hspace{3pt}} T' |$ in a couple of examples.

Example. Polar coordinates:

$$\displaystyle\int_B f( x, y ) dA = \displaystyle\int\displaystyle\int f( r {\rm \hspace{3pt} cos \hspace{3pt}} \theta, r {\rm \hspace{3pt} sin \hspace{3pt}} \theta ) {\bf R} dr d \theta,$$

$$T( r, \theta ) = ( r {\rm \hspace{3pt} cos \hspace{3pt}} \theta, r {\rm \hspace{3pt} sin \hspace{3pt}} \theta )$$

$$T'( r, θ ) = \left| \begin{array}{} {\rm \hspace{3pt} cos \hspace{3pt}} \theta & -{\rm \hspace{3pt} sin \hspace{3pt}} \theta \\ {\rm \hspace{3pt} sin \hspace{3pt}} \theta & r {\rm \hspace{3pt} cos \hspace{3pt}} \theta \end{array} \right|$$

and

$$\begin{array}{} | {\rm det \hspace{3pt}} T'( r, \theta ) | &= | {\rm \hspace{3pt} cos \hspace{3pt}} \theta r {\rm \hspace{3pt} cos \hspace{3pt}} \theta - {\rm \hspace{3pt} sin \hspace{3pt}} \theta ( -r {\rm \hspace{3pt} sin \hspace{3pt}} \theta ) | \\ &= | r {\rm \hspace{3pt} cos}^2 \theta + r {\rm \hspace{3pt} sin}^2 \theta | \\ &= r | {\rm cos}^2 \theta + {\rm \hspace{3pt} sin}^2 \theta | \\ &= r. \end{array}$$

Example. Rotation, rotated through $\alpha$

$$T' = \left| \begin{array}{} {\rm \hspace{3pt} cos \hspace{3pt}} \alpha & -{\rm \hspace{3pt} sin \hspace{3pt}} \alpha \\ {\rm \hspace{3pt} sin \hspace{3pt}} \alpha & {\rm \hspace{3pt} cos \hspace{3pt}} \alpha \end{array} \right|$$

$${\rm det \hspace{3pt}} T' = {\rm \hspace{3pt} cos}^2 \alpha + sin^2 \alpha = 1, $$

no stretching.

Review exercise. Consider

$$\displaystyle\int\displaystyle\int_{B(0,1)} x^2 y^2 dA,$$

convert to iterated integral:

$$\displaystyle\int_{-1}^1 \displaystyle\int_{\sqrt{1-x^2}}^{\sqrt{1-x^2}} x^2 y^2 dy dx$$

Consider a more general situation. Suppose

$T: {\bf R}^2 \rightarrow {\bf R}^2$ is linear.

Then

$${\rm area \hspace{3pt}} B = || v_1 × v_2 || {\longleftrightarrow} v_1 = \left| \begin{array}{c} (*) \\ (*) \\ 0 \end{array} \right|, v_2 = \left| \begin{array}{c} (*) \\ (*) \\ 0 \end{array} \right|$$

Further

$$v_1 = T( e_1 ), v_2 T( e_2 ).$$

Now

$$T( u, v ) = \left| \begin{array}{} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| \left| \begin{array}{} u \\ v \end{array} \right|$$

then

$$v_1 = T( e_1 ) = \left| \begin{array}{} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| \left| \begin{array}{} a_{11} \\ a_{21} \end{array} \right|$$

and

$$v_1 = T( e_2 ) = \left| \begin{array}{} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| \left| \begin{array}{} 0 \\ 1 \end{array} \right| = \left| \begin{array}{} a_{12} \\ a_{22} \end{array} \right|$$

Substitute: $$\begin{array}{} {\rm area \hspace{3pt}} B &= || v_1 \times v_2 || \\ &= \left\| \begin{array}{} |a_{11}| \times |a_{12}| \\ |a_{21}| \times |a_{22}| \\ |0| \times |0| \end{array} \right\| \\ &= \left \| {\rm \hspace{3pt} det \hspace{3pt}} \left| \begin{array}{} a_{11} & a_{12} & i \\ a_{21} & a_{22} & j \\ 0 & 0 & k \end{array} \right| \right\| \\ &= || 0i + 0j + {\rm \hspace{3pt} det \hspace{3pt}} M_t k|| \\ &= |{\rm det \hspace{3pt}} M_t|, \end{array}$$

where $M_t$ is the matrix of $T$.

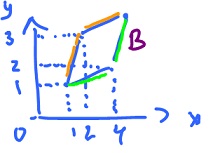
Theorem.

area $T(Q) = | {\rm det}( M_t ) |$

where $T$ is affine, $M_t$ is its matrix, $Q$ the unit square.

Riemann sum of $f$ equals

$$\displaystyle\sum_i f( x_i, y_i ) {\Delta}A,$$

where ${\Delta}A$ are the areas of the parallelograms.

Transform it to the Riemann sum over $( u, v )$

$$\displaystyle\sum_i f( T( u, v_i ) ) | {\rm det \hspace{3pt}} T' | {\Delta}W,$$

where ${\Delta}W$ is the area of the squares.

Theorem. If $T$ is an affine function $T: {\bf R}^2 \rightarrow {\bf R}^2$, and $Q$ a square, $B = T(Q)$, then

$$\displaystyle\int\displaystyle\int_{B=T(Q)} f( x, y ) dA = \displaystyle\int\displaystyle\int_Q f( T( u, v ) ) | det T' | dW.$$

Problem. Suppose $B$ is the parallelogram on the right. Evaluate

$$\displaystyle\int\displaystyle\int_B x^2 y dA. $$

We could solve the problem by applying iterated integral with these bounds as graphs bounding $B$ from below and above. But instead we will simplify $B$, then integrate over $Q$.

How do we transform $B$ into the unit square? We need to find $S: {\bf R}^2 \rightarrow {\bf R}^2$ such that

$$S(B) = Q.$$

Turns out $T = S^{-1}$ if

$$T( u, v ) = \left| \begin{array}{} 1 & 3 \\ 2 & 1 \end{array} \right| \left| \begin{array}{} u \\ v \end{array} \right| + \left| \begin{array}{} 1 \\ 1 \end{array} \right|.$$

To verify that $T$ is an invertible function, check:

$${\rm det \hspace{3pt}} T {\neq} 0, $$

Indeed:

$$| det T | = \left| \begin{array}{} 1 & 3 \\ 2 & 1 \end{array} \right| = | 1 - 6 | = 5.$$

We have $f( x, y ) = x^2 y$ and

$$\displaystyle\int\displaystyle\int_B x^2 y dA = \displaystyle\int\displaystyle\int_Q f T( u, v ) 5 dW {\rm \hspace{3pt} (iterated)}$$

Then

$$\begin{array}{} f T( u, v ) &= f \left( \left| \begin{array}{} 1 & 3 \\ 2 & 1 \end{array} \right| \left| \begin{array}{} u \\ v \end{array} \right| + \left| \begin{array}{} 1 \\ 1 \end{array} \right| \right) \\ &= f( u + 3v + 1, 2u + v + 1 ) \\ &= ( u + 3v + 1)^2 ( 2u + v + 1 ), \end{array}$$

hence

$$\displaystyle\int\displaystyle\int_B x^2 y dA = \displaystyle\int_0^1 \displaystyle\int_0^1 ( u + 3v + 1 )^2 ( 2u + v + 1 ) du dv.$$

The rest of the calculation is routine.

Let's recall that we had an analogue of this construction in Calc 1 (${\rm dim \hspace{3pt}} 1$). Consider how we compute this (definite!) integral in two ways:

$$\displaystyle\int_0^1 2x e^{x^{2}} dx.$$

In either case we use change of variables.

(1) We use the substitution:

$$u = x^2, du = 2xdx.$$

to compute the antiderivative (with respect to $x$):

$$\displaystyle\int 2x e^{x^{2}} dx= \displaystyle\int e^u du = e^u + c = e^{x^{2}} + C,$$

and then apply the Fundamental Theorem of Calculus with respect to $x$:

$$\displaystyle\int_0^1 2x e^{x^{2}} dx = e^{x^{2}} |_0^1 = e - 1.$$

(2) Alternatively, we use the same substitution to get

$$\displaystyle\int_{x=0}^{x=1} 2x e^{x^{2}} dx = \displaystyle\int_{u=0}^{u=1} e^u du$$

but don't do "the back-substitution" and then apply the Fundamental Theorem of Calculus with respect to $u$:

$$= \displaystyle\int_0^1 e^u du $$ $$= e^u |_0^1 $$ $$= e^1 - e^0.$$

Exercise. A similar example for integration over a disk:

$$\displaystyle\int\displaystyle\int_{B(0,1)} x^2 y^2 dA,$$

with

$$\left. \begin{array}{} x = r {\rm \hspace{3pt} cos \hspace{3pt}} \theta | \\ y = r {\rm \hspace{3pt} sin \hspace{3pt}} \theta | \end{array} \right| T$$

and $| {\rm det \hspace{3pt}} T' | = r.$

Further

$$\begin{array}{} \displaystyle\int_0^{2 \pi} \displaystyle\int_0^1 (r {\rm \hspace{3pt} cos \hspace{3pt}} \theta )^2 (r {\rm \hspace{3pt} sin \hspace{3pt}} \theta )^2 r dr d \theta &= \displaystyle\int_0^{2 \pi} \displaystyle\int_0^1 r^5 {\rm \hspace{3pt} cos \hspace{3pt}} \theta {\rm \hspace{3pt} sin \hspace{3pt}} \theta dr d \theta \\ &= \displaystyle\int_0^{2 \pi} {\rm \hspace{3pt} cos}^2 \theta {\rm \hspace{3pt} sin}^2 \theta d \theta \displaystyle\int_0^1 r^5 dr \\ &= ... \end{array}$$

substitute $u = {\rm \hspace{3pt} sin \hspace{3pt}} \theta$ and complete the computation.

What if $F$ is not affine?

Then find the best affine approximation $T$ of $F$, at each point $( a, b )$. Which means that

$$F'( a, b ) = T'( a, b ).$$

This approximation applies to every element of the Riemann sum, i.e., on each of the rectangles $R_{ij}$, in total (using the limit and the additivity property):

$$\displaystyle\sum_{i,j} \displaystyle\int\displaystyle\int_{R_{ij}} f( T( u, v )) | {\rm det \hspace{3pt}} T'( a, b )| dW = \displaystyle\int\displaystyle\int_{R_{ij}} f( T( u, v )) | det T'( u, v )| dW$$

And the result is:

$$\displaystyle\int\displaystyle\int_{B=T(Q)} f( x, y ) dA = \displaystyle\int\displaystyle\int_Q f( T( u, v )) | {\rm \hspace{3pt} det}' T( u, v )| dW.$$

Also Integration by substitution: examples.