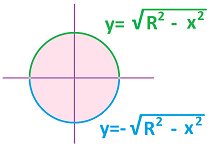Integration

Linear change of variables in integral

Let's review what we know about integrals.

Suppose a function $f$ is defined on an open interval $I$. Then a function $F$ defined on $I$ that satisfies $F' = f(x)$ for all $x$ is called an antiderivative of $f$.

We can think of the definition as an equation for functions: $$\begin{array}{|l|}\hline\quad \text{Given } f, \text{ solve for } F:\quad F'=f.\quad \\ \hline\end{array}$$ This equation has infinitely many solutions when $f$ is integrable. Furthermore, according to the Anti-differentiation Theorem, if $F$ is one of its antiderivatives, then the set of all antiderivatives of $f$ is $$\{F+C:\ C \text{ real }\}.$$

The Riemann integrals defined and studied in Chapter 11 is linked to antiderivatives by the following.

Theorem (Fundamental Theorem of Calculus). (I) Given a continuous function $f$ on $[a,b]$, the function defined by $$F(x) = \int_{a}^{x} f \, dx $$ is an antiderivative of $f$ on $(a,b)$. (II) For any integrable function $f$ on $[a,b]$ and any of its antiderivatives $F$, we have $$\int_{a}^{b} f \, dx =F(b)-F(a).$$

Numerous quantities are defined via the Riemann sums: areas and displacements as presented in Chapter 11 and weights, volumes, lengths, fluxes, work, and many more to be presented in Chapter 13. The latter part of the theorem allows us to compute anything defined this way by means of a simple substitution -- as long as an antiderivative can be found! We will refer to them as indefinite integrals or simply integrals.

How do we find integrals? This is the subject of the present chapter.

From Chapter 9, we borrow some facts about integrals.

Elementary integrals: $$\begin{array}{rll} \int x^{s}\, dx&= \frac{1}{s + 1} x^{s + 1}+C, \quad \text{ for }s \neq -1;\\ \int \frac{1}{x}\, dx&= \ln |x|+C, \ x > 0 \text{ or } x<0;\\ \int e^{x}\, dx&= e^{x}+C;\\ \int \sin x\, dx&= -\cos x +C;\\ \int \cos x\, dx&=\sin x+C. \end{array}$$

Sum Rule: $$\int (f+g)\, dx=\int f\, dx+\int g\, dx.$$

Constant Multiple Rule: $$\int (cf)\, dx=c\int f\, dx.$$

Linear Composition Rule: $$\int f(mx+b)dx=\tfrac{1}{m}\int f(t)\, dt\Big|_{t=mx+b}.$$

In this section, we will further examine the last result.

Recall that we can interpret every composition as a change of variables. We are especially interested in a change of units because we often measure quantities in multiple ways:

• length and distance: inches, miles, kilometers, light years;
• time: minutes, seconds, hours, years;
• weight: pounds, kilograms, karats;
• temperature: degrees of Celsius, of Fahrenheit,
• etc.

In fact, the conversion formulas (some of them examined below) for the changes of units listed above are all linear. This is why the Linear Composition Rule for derivatives and integrals provides a simple answer to the question: how does such a change affect integral calculus as we know it? There will be a single conversion coefficient.

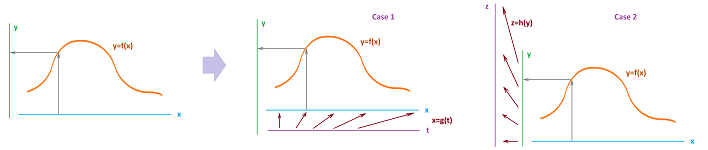
Suppose a function $$y=f(x)$$ establishes a relation between two quantities $x$ and $y$: $$x \xrightarrow{\quad f \quad}y.$$ Now, either one may be replaced with a new variable (or a new unit). Let's call them $t$ and $z$ respectively and suppose these replacements, i.e., substitutions, are given by some functions:

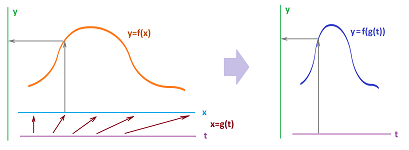
• Case 1: $x=g(t)$; and
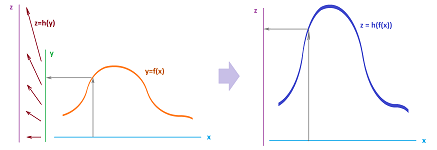
• Case 2: $z=h(y)$.

These substitutions create new relations: $$\begin{array}{lll} \text{Case 1}:&t& \xrightarrow{\quad g \quad}& x &\xrightarrow{\quad f \quad}&y;\\ \text{Case 2}:&&&x &\xrightarrow{\quad f \quad}& y& \xrightarrow{\quad h \quad} &z. \end{array}$$ Let's call this composition $k$:

• Case 1: $y=k(t)=f(g(t))$; or
• Case 2: $z=k(x)=h(f(x))$.

The two cases are visible in the picture below:

Case 1. The change of units is $$x=g(t)=mt+b.$$

Theorem (Linear Composition Rule I). For any numbers $m\ne 0$ and $b$ and any integrable function $f$, we have: $$\int f(mt+b)\, dt=\tfrac{1}{m}\int f(x)\, dx\Big|_{x=mt+b}.$$

Example (time shift). If $x$ is time and we change the moment from which we start measuring time, we have: $$g(t)=t+t_0\ \Longrightarrow\ \int k \, dt=\int f(t+t_0) \, dt.$$ $\square$

Example (seconds to minutes). Suppose $x$ is time and $y$ is the location. If $x$ is measured in seconds, then switching to time $t$ measured in minutes will require a function: $$x=g(t)=60t.$$ We know from Chapter 8 that the graphs of the quantities describing motion are simply re-scaled versions of the old ones. Let's recast this statement in the integral form.

• Suppose $y=q(t)$ and $y=p(x)$ are the location as functions of minutes and seconds respectively. Then

$$q(t)=p(60t).$$

• Suppose $v(t)=q'(t)$ and $e(x)=p'(x)$ are the velocities as functions of minutes and seconds respectively. Therefore, $\int v \, dt=q$ and $\int e\, dx=p$. We substitute these into the above equation:

$$\int v \, dt=\int e\, dx\Bigg|_{x=60t}.$$ $\square$

Exercise. Express the location as a function of minutes in terms of the velocity as a function of seconds.

Case 2. The change of units is $$z=h(y)=my+b.$$

Theorem (Linear Composition Rule II). For any numbers $m$ and $b$ and any integrable function $f$, we have: $$\int \big( mf(x)+b \big) \, dx=m\int f \, dx+bx.$$

Example (space shift). If $y$ is the location and we change the place from which we start measuring, we have: $$h(x)=y+y_0\ \Longrightarrow\ \int k \, dx=\int f \, dx+y_0x.$$ If we change the direction of the $x$-axis, we have: $$h(x)=-y\ \Longrightarrow\ \int k \, dx=-\int f \, dx.$$ $\square$

Example (miles to kilometers). Suppose $x$ is time and $y$ is the location, then function $h$ may represent the change of units of length, such as from miles to kilometers: $$z=h(y)=1.6y.$$ As we know, the quantities describing motion are simply replaced with their multiples. The new graphs are the vertically stretched versions of the old ones. Let's recast this statement in the integral form:

• if $a$ is the acceleration with respect to miles, then the velocity with respect to kilometers is $\frac{1}{1.6}\int a \, dx$;
• if $v$ is the velocity with respect to miles, then the location with respect to kilometers is $\frac{1}{1.6}\int v \, dx$.

$\square$

Exercise. Prove the above formulas.

Example (time and temperature). This is how both cases can appear. Recall the example from Chapter 8 when we have a function $f$ that records the temperature -- in Fahrenheit -- as a function $f$ of time -- in minutes -- replaced with another that records the temperature in Celsius as a function $g$ of time in seconds:

• $s$ time in seconds;
• $m$ time in minutes;
• $F$ temperature in Fahrenheit;
• $C$ temperature in Celsius.

The conversion formulas are: $$m=s/60,$$ and $$C=(F-32)/1.8.$$

These are the relations between the four quantities: $$g:\quad s \xrightarrow{\quad s/60 \quad} m \xrightarrow{\quad f\quad} F \xrightarrow{\quad (F-32)/1.8\quad} C.$$ And this is the new function: $$F=k(s)=(f(s/60)-32)/1.8.$$ Then, we have: $$\begin{array}{lll} \int k\, ds &=\int \big( (f(s/60)-32)/1.8 \big)\, ds\\ &=\int f(s/60)/1.8 \, ds - \int 32/1.8 \, ds\\ &=\frac{1}{1.8}\int f(s/60) \, ds - 32/1.8s\\ &=\frac{60}{1.8}\int f\, dm \Bigg|_{m=s/60} - 32/1.8s, \end{array}$$ by the Linear Composition Rule. $\square$

Exercise. Provide a similar analysis for the sizes of shoes and clothing.

Example (degrees to radians). The conversion of the number of degrees $y$ to the number of radians $x$ is: $$x=\frac{\pi}{180}y.$$ Then, for any function $z=f(x)$, we have: $$\int f\left( \frac{\pi}{180}y \right)\, dy=\frac{180}{\pi}\int f \, dx \Bigg|_{x=\frac{\pi}{180}y}.$$ Because of the extra coefficient, the trigonometric integration formulas, such as $\int \sin x \, dx=-\cos x+C$, don't hold for degrees. Indeed, if we denote sine and cosine for degrees by $\sin_dy$ and $\cos_dy$ respectively, we have: $$\sin_dy=\sin \left( \frac{\pi}{180}y \right) \text{ and } \cos_dy=\cos \left( \frac{\pi}{180}y \right).$$ Therefore, $$\begin{array}{lll} \int \sin_dy\, dy&=\frac{180}{\pi}\int \sin x\, dx \Bigg|_{x=\frac{\pi}{180}y}\\ &=\frac{180}{\pi} \cos x \Bigg|_{x=\frac{\pi}{180}y}+C\\ &=\frac{180}{\pi} \cos_d y +C. \end{array}$$ $\square$

Example (logarithmic scale). The following non-linear change of units is called a logarithmic scale: $$x=g(t)=10^t.$$ Then, for a function $y=f(x)$, suppose $F$ is its antiderivative. How do we, as we did above, express antiderivatives of $y=f(10^t)$ in terms of $F$? We would like to have a formula: $$\int f(10^t)\, dt=...$$ We proceed as before, by the Chain Rule: $$\frac{d(F\circ g)}{dt}=\frac{dF}{dx}\Bigg|_{x=10^t}\cdot \left( 10^t \right)'=f(10^t)10^t\ln 10.$$ Therefore, $$F(10^t)=\int f(10^t)\cdot 10^t\ln 10 \, dt,$$ and, further, $$\int f(10^t)\cdot 10^t \, dt=\frac{1}{\ln 10}F(10^t).$$ Unfortunately, the presence of the factor $10^t$ inside the integral seems to not allow us to finish the job and express directly antiderivatives of $y=f(10^t)$ in terms of $F$. We will need further analysis... $\square$

Integration by substitution: compositions

How do we integrate functions with compositions and not just linear?

Just as with other integration formulas we, again, try to “reverse” the direction of differentiation.

Let's take $\sin (x^{2})$. It is easy to differentiate by the Chain Rule: $$\left( \sin (x^{2}) \right)' = \cos (x^{2}) \cdot 2x .$$ We would like to have a similar formula for the integral of this function: $$\int \sin (x^{2}) \, dx = ? $$ But we don't recognize $\sin (x^{2})$ as the derivative of any function we know...

We do recognize $\cos (x^{2}) \cdot 2x$ however, from two lines above! Then, $$\int\cos (x^{2}) \, 2x \, dx = \sin (x^{2}) + C .$$ More examples? Here they are: $$\int\sin (x^{2}) \, 2x \, dx = -\cos (x^{2}) + C , \quad \int e^{x^{2}} \, 2x \, dx = e^{x^{2}} + C .$$

Three examples, what do they have in common? We see a pattern: $$\begin{array}{lll} \int & \cos & (x^{2}) & \cdot 2x & dx &= &\sin & (x^{2})\\ \int & \sin & (x^{2}) & \cdot 2x & dx &= &-\cos & (x^{2})\\ \int & e & ^{(x^{2})} & \cdot 2x & dx &= &e & ^{(x^{2})}\\ \int & ? & (x^{2}) & \cdot 2x & dx &= &? & (x^{2}) \end{array}$$ Everything is the same except whatever is behind these question marks.

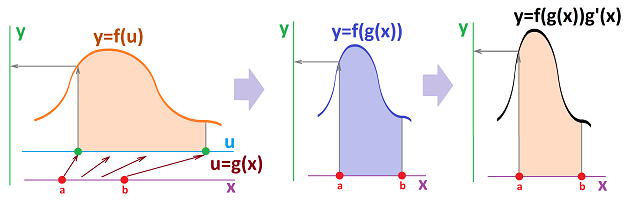
We know what is missing and we rewrite: $$ \int f(x^{2}) \cdot 2x \, dx = F(x^{2}) + C, $$ where $F$ is an antiderivative of $f$: $$F' =f .$$ So, to integrate these we need to solve this problem: given $f$, find $F$. This is, of course, integration but not with respect to $x$! Let's say $f$ and $F$ are functions of some $u$, an intermediate variable, given by: $$u=g(x).$$ Then to find $F$, we integrate $f$ with respect to $u$: $$F(u) = \int f(u)\, du .$$ This is a change of variables!

Example. Evaluate: $$\int \underbrace{\sqrt[3]{x^{2}}}_{\text{decompose}}\cdot 2x \, dx = ?$$ The key step is to break the composition apart, to find $u,f,F$. So, $u=x^2,\ f(u)=u^{1/3}$. Then, $$F(u) = \int \sqrt[3]{u}\, du = \int u^{\frac{1}{3}} \, du\ \overset{\text{PF}}{=\! =\! =\! =} \frac{u^{\frac{1}{3}+1}}{\frac{1}{3} + 1} + C = \frac{3}{4}u^{\frac{4}{3}} + C.$$ Even though integration is finished, this isn't the answer because it has to be a function of $x$! We need to substitute $u=x^2$ back into this function: $$F(x^2) = \frac{3}{4}\left(x^2\right)^{\frac{4}{3}} + C.$$ $\square$

For a more general analysis, we replace $x^{2}$ with $g(x)$. We are prepared to integrate this: $$\int f(g(x))\cdot g'(x)\, dx.$$ Then the answer is $F(g(x))$, where $F$ is an antiderivative of $f$: $$F' = f.$$

Theorem (Integration by Substitution). Given a continuous function $f$ and a differentiable function $g$, we have: $$\int f(g(x))\cdot g'(x)\, dx=F(g(x))+C,$$ where $F$ is any antiderivative of $f$.

Proof. $$\begin{array}{lrl} \left( F(g(x)) \right)' &\overset{\text{CR}}{=\! =\! =\! =} &F'(g(x)\cdot g'(x) \\ &= &f(g(x))g'(x). \end{array}$$ $\blacksquare$

Conclusion: we can integrate compositions when

• the derivative of the “inside” function is present as a factor.

In other words, as a prerequisite, we need to have the following: $$\int f(\underbrace{g(x)}_{\text{inside function}}) \cdot \underbrace{g'(x)}_{\text{its derivative}} \, dx.$$

Example. Evaluate $$\int \sqrt{x^{3} + 1} \cdot 3x^{2} \, dx .$$ Observe first that the derivative of the function inside is present: $$(x^{3} + 1)'=3x^2.$$ So, the theorem should work... $$\begin{array}{lll} \text{decomposition: } & \text{integration:}\\ f(u) = \sqrt{u} & \Longrightarrow F(u) = \int u^{\frac{1}{2}} \, du = \frac{2}{3} u^{\frac{3}{2}} + C \\ u = g(x) = x^{3} + 1 &\Longrightarrow g'(x) = 3x^{2} \\ \text{back-substitution: } & F(g(x))= \frac{2}{3}(x^{3} + 1)^{\frac{3}{2}} + C \end{array}$$ Note how we converted the original integral to a simpler one, with respect to $u$. $\square$

Example. Evaluate $$\int \sqrt{x^{3} + 1} \cdot x^{2} \, dx = ? $$ Just notice that $(x^{3} + 1 )' = 3x^{2}$, not $x^{2}$. The condition doesn't seem to be satisfied anymore... However, this function is just a constant multiple of the one in the last example and so, therefore, is the integral. We will ignore this shortcut though.

We'll try to apply the Integration by Substitution formula anyway: $$\left. \begin{aligned} \text{first substitution: } u &= x^{3} + 1 \\ \text{second substitution: } u' &= 3x^{2} .\\ \end{aligned} \right\} \begin{array}{lll} \text{ we convert the integral with respect to } x \\ \text{ to a new one with respect to } u\end{array}$$ The hope is that the new integral will be simpler than the original.

We already have all we need here. We break what's inside the integral apart but not in the obvious way: $$\sqrt{x^{3} + 1} = \sqrt u, \quad x^{2} = \frac{1}{3} u'.$$ Now we deal with the integral itself. $$\begin{array}{lrl} \int\underbrace{ \sqrt{x^{3} + 1}}_{u \text{ inside}} \, x^{2} \, dx &=&\int \sqrt{u} \cdot \frac{1}{3}\, du & \\ & = &\frac{1}{3}\int u^{\frac{1}{2}}\, du \, & \gets\text{ new integral!} \\ & \overset{\text{PF}}{=\! =\! =}&\frac{1}{3} \, \frac{2}{3} u^{\frac{3}{2}} + C \, &\gets \text{ integration finished!} \\ &=& \frac{1}{3} \, \frac{2}{3} (x^{3} + 1)^{\frac{3}{2}} + C \, &\gets \text{back-substitution } u = x^{3} + 1. \end{array}$$ Answer: $$\int \sqrt{x^{3} + 1} \, x^{2} \, dx =\frac{2}{9} (x^{3} + 1)^{\frac{3}{2}} + C.$$ $\square$

Exercise. Evaluate $$\int \sqrt{x^{3} + 1} \, x^{2} \, dx. $$

Exercise. Evaluate $$\int \sqrt{x^{4} + 1} \, x^{3} \, dx. $$

We can re-write the formula as follows: $$\begin{array}{|c|}\hline \quad \int f(g(x))\cdot g'(x)\, dx=\int f(u)\, du\Bigg|_{u=g(x)}. \quad \\ \hline\end{array}$$ In this version there is no confusion about whether the integration in the right-hand side has been carried out.

The simplest kind of integral for which this approach always works involves a linear change of variables. If $$g(x)=mx+b,\ m\ne 0,$$ our formula becomes: $$\int f(mx+b)\cdot m\, dx= \int f(u)\, du\Bigg|_{u=mx+b}.$$ We consequently recover the familiar Linear Composition Rule: $$\int f(mx+b)\, dx= \frac{1}{m}\int f(u)\, du\Bigg|_{u=mx+b}.$$

Example. Evaluate: $$\int e^{3x}\, dx=\frac{1}{3}\int e^u\, du\Bigg|_{u=3x}=\frac{1}{3}e^u+C\Bigg|_{u=3x}=\frac{1}{3}e^{3x}+C.$$ $\square$

Example. Evaluate: $$\int e^{x} \sin (e^{x}) \, dx.$$ Let's break the composition, $\sin(e^{x})$, that we see: $$ u = e^{x}, \quad y = \sin u. $$ Furthermore, $$u' = e^{x} . $$ Use these two: $$\begin{array}{lll} \int e^{x} \sin (e^{x}) \, dx &=& \int \sin u \, du &\text{ ...evaluate } \\ &=& -\cos u + C &\text{ ...substitute}\\ &=& \cos e^{x} + C. \end{array}$$ $\square$

Exercise. Evaluate: $$\int \sqrt{\sin x}\cdot \cos x\, dx.$$

Exercise. Evaluate: $$\int e^{e^x+x}\, dx.$$

Example. $$\begin{array}{lllll} \int \tan x \, dx &= & \text{ What, no composition?! } \\ &= \int \frac{\sin x}{\cos x} \, dx & \text{ ...there is division though...}\\ &= \int \sin x\cdot\frac{1}{\cos x} \, dx & \text{ ...there is multiplication in fact...}\\ &= \int \sin x\left(\cos x\right)^{-1} \, dx & \text{ ...there is composition after all...}\\ &= -\int \left( \cos x \right)' \left( \cos x \right)^{-1} \, dx & \text{ ...and the derivative of the inside function too...}\\ &= -\int \left( u \right)^{-1} \, du & \text{ ...the formula applies with } u=\cos x...\\ &= -\ln u+C & \text{ ...integrate... } \\ &= -\ln \cos x+C & \text{ ...back-substitute. } \end{array}$$ $\square$

Change of variables in integrals

Example. Let's take another look at: $$\int xe^{x^2}\, dx=\frac{1}{2}\int e^u \, du=e^u+C=e^{x^2}+C.$$ It works so well! Changing the power, $x$ to $x^2$, ruins this nice arrangement: $$\int x^2e^{x^2}\, dx=\int ue^u\,dx =...\text{ now what?}$$ In fact, no power of $x$ other than $1$: $$\int x^3e^{x^2}\, dx=?\quad \int x^4e^{x^2}\, dx=?\quad \int x^{1/2}e^{x^2}\, dx=?\quad \int x^\pi e^{x^2}\, dx=?$$ will allow integration by substitution according to the formula. $\square$

Warning: do not replace $x$ in $dx$ with $u$, $dx\ne du$!

We still would like to be able to convert an integral to a new variable. It is always possible! The challenge is what to do with $dx$...

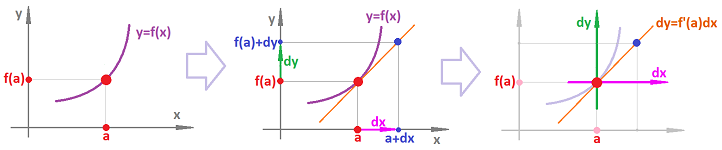
We have to look at the integral differently. What exactly do we integrate? In the integral, $$\int k(x)\, dx,$$ it has been a function, $k(x)$, while $\int$ and $dx$ serve as mere brackets... This doesn't work anymore! We need to make sense of $dx$. Significantly, we switch from a function to a differential form, $k(x)\cdot dx$. As presented in Chapter 8, the form comes from the following: $$y=f(x) \text{ at }x=a\ \Longrightarrow\ \frac{dy}{dx}=f'(a),$$ and, furthermore, $$\qquad \Longrightarrow\ \ dy=f'(a)\cdot dx.$$ This is a relation between the two extra variables, nothing but numbers, once the relation between the old ones has been specified:

In the graph, $dx$ is the run and $dy$ is the rise of the tangent line. They are called the differentials of $x$ and $y$ respectively. The dependence between them varies from location to location. This is further discussed in Chapter 14.

Back to integration... So, $dx$ is the differential of $x$, which is a variable separate from, but related to, $x$. Then, $f'(x)\cdot dx$ is just a function of two variables. The dependence of the differential form on the second variable is especially simple; it's a multiple.

Now integration by substitution... The differential $du$ of $u$ is a variable separate from, but related to, $u$. So, changing variables means going from $x$ to $u$ and from $dx$ to $du$. Handling the differentials is a separate step in the process of changing the variable.

Recall how the Chain Rule, in the Leibniz notation, is interpreted as, and it is, a “cancellation” of $du$ (when it's not zero): $$\frac{dy}{dx}=\frac{dy}{\not du}\frac{\not du}{dx}.$$ A similar idea applies to integrals. We take the formula of integration by substitution: $$\int f(g(x))\cdot g'(x)\, dx=\int f(u)\, du\Bigg|_{u=g(x)},$$ and switch to the Leibniz notation, subject to the substitution: $$\int f(u)\cdot \frac{du}{\not dx}\, \not dx=\int f(u)\, du.$$ Note how $dx$ “cancels” turning the integral with respect to $x$ to one with respect to $u$. We take this idea one step further...

Corollary (Change of variables). Under a substitution $u=g(x)$ in an integral, we also substitute: $$\begin{array}{|c|}\hline \quad du=g'\, dx. \quad \\ \hline\end{array}$$

This formula is used -- in addition to $u=g(x)$ -- in order to complete the substitution.

Example. Let's apply the formula to the example from the last section: $$\int e^{x} \sin (e^{x}) \, dx.$$ We start with a substitution this time: $$ u = e^{x}\ \Longrightarrow\ du = e^{x}dx \ \Longrightarrow\ dx=\frac{du}{e^x}. $$ Substitute both the first and the last of these into the integral: $$\begin{array}{lll} \int e^{x} \sin (e^{x}) \, dx &=&\int e^{x} \sin e^x \, \frac{du}{e^x} & \text{...substitute the last and cancel...}\\ &=&\int \sin u \, du & \text{...substitute the first and the change of variable is complete!}\\ &=& -\cos u + C &\text{...the rest is a bonus.}\\ &=& -\cos e^{x} + C. \end{array}$$ $\square$

With the formula, we can change variables in any integral, even the kind that's not subject to integration by substitution.

Example. Let's evaluate: $$\int x^2e^{x^2}\, dx=?$$ The change of variables is the same as before ($x\ge 0$): $$u=x^2 \ \Longrightarrow\ du=2x\, dx \ \Longrightarrow\ dx=\frac{du}{2x}.$$ However, in anticipation that the cancellation might not be as easy as last time, we also find the inverse substitution (literally the inverse of the substitution function): $$u=x^2 \ \Longrightarrow\ x=\sqrt{u}.$$ We have three substitutions:

• 1. $x^2=u$;
• 2. $dx=\frac{du}{2x}$; and
• 3. $x=\sqrt{u}$.

Substitute: $$\begin{array}{ll} \int x^2e^{x^2}\, dx&=\int x^2 e^u\, dx&\text{#1}\\ &=\int x^2 e^u\, \frac{du}{2x}&\text{#2}\\ &=\int \left(\sqrt{u}\right)^2 e^u\, \frac{du}{2\sqrt{u}}&\text{#3}\\ &=\frac{1}{2}\int \sqrt{u} e^u\, du. \end{array}$$ Even though the change of variables hasn't made the integral easier to integrate, the conversion is complete! $\square$

We can have any substitution in any integral.

Example. Let's pick a wrong change of variables in the familiar integral: $$\int xe^{x^2}\, dx=?$$ This substitution is chosen even though we don't anticipate that it will simplify the integral: $$\# 1.\ u=x^3 .$$ The differential is found: $$\# 2.\ u=x^3 \ \Longrightarrow\ du=3x^2\, dx \ \Longrightarrow\ dx=\frac{du}{3x^2}.$$ The inverse substitution is found: $$\# 3.\ x=u^{1/3}.$$ Substitute: $$\begin{array}{ll} \int xe^{x^2}\, dx&=\int x e^{(u^{1/3})^2}\, dx&\text{#3}\\ &=\int x e^{u^{2/3}}\, \frac{du}{3x^2}&\text{#2}\\ &=\int u^{1/3} e^{u^{2/3}}\, \frac{du}{3\left(u^{1/3}\right)^2}&\text{#3}\\ &=\frac{1}{3}\int u^{-1/3} e^{u^{2/3}}\, du. \end{array}$$ $\square$

Exercise. Carry out the substitution $u=x^4$ in the above integral.

Exercise. Carry out the substitution $u=x$ in the above integral.

Exercise. Make up your own integral and carry out the substitution $u=x^2$. Repeat.

Example. If we hope to simplify the integral, the substitution should be the “inside” function of the composition. For example, consider: $$\int \sqrt{x+1}\cdot x\, dx.$$ We choose $u=x+1$. Then, $du=dx$. Therefore, $$\begin{array}{lll} \int \sqrt{x+1}\cdot x\, dx &= \int u^{1/2}(u-1)\, du&\text{ is it any better?..}\\ &=\int u^{1/2}u\, du+\int u^{1/2}(-1)\, du&\text{ yes!}\\ &=\int u^{3/2}u\, du-\int u^{1/2}\, du\\ &=\frac{2}{5}u^{5/2}-\frac{2}{3}u^{3/2}+C\\ &=\frac{2}{5}(x+1)^{5/2}-\frac{2}{3}(x+1)^{3/2}+C. \end{array}$$ $\square$

Example. Let's revisit the issue of converting units to a logarithmic scale: $$x=10^t.$$ Then, $$dx=10^t \ln 10 \, dt \ \Longrightarrow\ dt=\frac{dx}{10^t \ln 10}.$$ Substitute into the integral and simplify: $$\int f(10^t)\, dt=\int f(x)\, \frac{dx}{10^t \ln 10} =\frac{1}{\ln 10}\int f(x) \frac{1}{x}\, dx.$$ We have expressed the integral of $y=f(10^t)$ as an integral with respect to $x$. $\square$

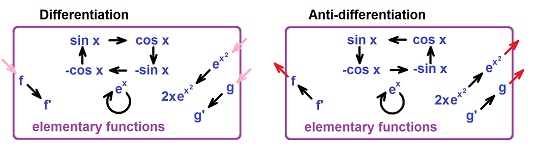
This is the summary of what is going on. We start with a familiar diagram for the Chain Rule of differentiation: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccccccccc} & f(g(x))g'(x) &\la{\frac{d}{dx}} & F(g(x)) \\ &\quad \ua{\text{CR}} & &\ \ \da{u=g(x)}&\small\text{substitution } \\ & f(u) &\la{\frac{d}{du}} & F(u) \end{array}$$ And then we make the diagram about integration by reversing the horizontal arrows: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccccccccc} & f(g(x))g'(x) &\ra{\int\ dx} & F(g(x)) \\ &\quad \ua{\text{CR}} & &\ \ \da{u=g(x)}&\small\text{substitution } \\ & f(u) &\ra{\int\ du} & F(u) \end{array}$$ Thus the change of variables method of integration gives us an alternative way of getting from top left to top right (integration with respect to $x$). We take a detour by following the counterclockwise path around the square: the Chain Rule formula in reverse, integration with respect to $u$, back-substitution.

Exercise. Execute the substitution $u=e^x$ for the integral (don't evaluate the resulting integral): $$\int \sin (1+e^x)\, dx.$$

Change of variables in definite integrals

What happens when we use substitution to evaluate definite integrals?

First, nothing has to change. After all, according to the Fundamental Theorem of Calculus, all we need is an antiderivative. So, to find the definite integral $$\int_a^b f(g(x))g'(x)\, dx,$$ find the corresponding indefinite integral first, as we did in the last section, $$H(x)=\int f(g(x))g'(x)\, dx,$$ if possible. If it is, then last step is as simple as it gets: $$\int_a^b f(g(x))g'(x)\, dx=H(b)-H(a).$$

Example. Let's evaluate: $$\int_0^1 e^{x} \sin (e^{x}) \, dx.$$ We have already found the antiderivative: $$\int e^{x} \sin (e^{x}) \, dx = -\cos e^{x} + C.$$ Therefore, $$\int_0^1 e^{x} \sin (e^{x}) \, dx = -\cos e^{1}-(- \cos e^{0})=-\cos e+ \cos 1.$$ Done! $\square$

A better question is, what happens to the definite integral under a change of variables, in addition to the substitutions presented in the last section?

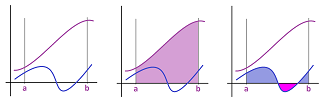
The substitution is just a transformation of the $x$-axis. It, therefore, shrinks/stretches the domain of integration:

So, we have to track, the end-points of the domain, i.e., the bounds of the integral, under our transformation.

Example. Let's take a closer look at the computation in the last example: $$\begin{array}{lll} \int e^{x} \sin (e^{x}) \, dx &= -\cos u+C&=-\cos e^{x} + C;\\ \int_0^1 e^{x} \sin (e^{x}) \, dx &= -\cos e^{1}- (-\cos e^{0})&=-\cos e+ \cos 1. \end{array}$$ It is done via the substitution $u=e^x$. We realize that we could have jumped from $-\cos u+C$ to $-\cos e+ \cos 1$ omitting the back substitution step in the upper right corner! Indeed: $$\cos u\Bigg|_1^e=-\cos e+ \cos 1.$$ We just need to see the relation between the bounds of the two integrals, with respect to $x$ and $u$: $$\begin{array}{lll} x=0\ \mapsto\ &u=e^0=1,\\ x=1\ \mapsto\ &u=e^1=e. \end{array}$$ The back-substitution becomes redundant. $\square$

So, under the change of variable $u=g(x)$, the domain of integration changes from

• $[a,b]$ for $x$ to
• $[g(a),g(b)]$ for $u$.

Even thought the stretch/shrink might be non-uniform, we only case about the end-points.

Example. Find the area under the graph of $y=x^2\cos x^3$ from $0$ to $2$. We have: $$\text{Area }=\int_0^{2} x^2\cos x^3\, dx.$$ The substitution first: $$u=x^3\ \Longrightarrow\ du=3x^2\, dx\ \Longrightarrow\ dx=\frac{du}{3x^2}.$$ Then, $$\int x^2\cos x^3\, dx=\int x^2\cos u\, \frac{du}{3x^2}=\frac{1}{3}\int \cos u\, du.$$ Now, what would this computation look like for the definite integral? Let's make it clear what variables we are referring to: $$\int_{x=0}^{x=2} x^2\cos x^3\, dx=\int_{x=0}^{x=2} x^2\cos u\, \frac{du}{3x^2}=\frac{1}{3}\int_{x=0}^{x=2} \cos u\, du.$$ We have mismatched variables! In order to fix that, we find the domain of integration by finding the bounds for $u$ from the corresponding bounds for $x$: $$\begin{array}{lll} x=0\ \mapsto\ &u=0^3=0,\\ x=2\ \mapsto\ &u=2^3=8. \end{array}$$ So, $[0,2]$ for $x$ becomes $[0,8]$ for $u$. Then, $$\int_{x=0}^{x=2} x^2\cos x^3\, dx=\frac{1}{3}\int_{x=0}^{x=2} \cos u\, du=\frac{1}{3}\int_{u=0}^{u=8} \cos u\, du.$$ The change of variables in the definite integral is complete! We don't have to go back to $x$ in order to finish the computation: $$\text{Area }=\frac{1}{3}\int_{u=0}^{u=8} \cos u\, du\ \overset{\text{FTC}}{=\! =\! =\! =}\ \sin u\Bigg|_{u=0}^{u=8}=\sin 8-\sin 0=\sin 8.$$ In summary, we showed that the areas of these two regions under these graphs -- $y=x^2\cos x^3$ and $y=\frac{1}{3} \cos u$ -- are equal and then found the latter one:

$\square$

Corollary (Definite Integration by Substitution). Under a substitution $u=g(x)$ in a definite integral, we have: $$\int_a^b f(g(x))\cdot g'(x)\, dx=F(u)\bigg|_{g(a)}^{g(b)}=F(g(b))-F(g(a)),$$ where $F$ is any antiderivative of $f$.

Proof. Recall the formula of integration by substitution: $$\int f(g(x))\cdot g'(x)\, dx=\int f(u)\, du\bigg|_{u=g(x)}=F(g(x)).$$ The formula follows now from the Fundamental Theorem of Calculus. $\blacksquare$

Here's another way to put it: $$\int_{x=a}^{x=b} f(g(x))\cdot g'(x)\, dx=\int_{u=g(a)}^{u=g(b)} f(u)\, du.$$

Corollary (Change of variables in definite integral). Under a substitution $u=u(x)$ in a definite integral, we have: $$\int_{a}^{b} f(u)\cdot \frac{du}{dx}\, dx=\int_{u(a)}^{u(b)} f(u)\, du.$$

Example. Let's carry out a change of variables in a definite integral without back-substitution. Consider $$\int_0^\pi\cos^2x\sin x\, dx.$$ The initial part -- choosing a substitution -- remains the same. We notice a composition and choose the function on the inside to be the substitution function for the new variable: $$\cos^2x=(\cos x)^2\ \Longrightarrow\ u=\cos x.$$ The second step is to find the rest of the substitution: $$u=\cos x\ \Longrightarrow\ du=-\sin x\, dx\ \Longrightarrow\ dx=\frac{du}{-\sin x}.$$ The next step is to find the corresponding bounds for $u$: $$\begin{array}{ll} x=\pi&\Longrightarrow&u=\cos \pi=-1;\\ x=0&\Longrightarrow&u=\cos 0=1.\\ \end{array}$$ We convert the integral to $u$ now and then evaluate it: $$\begin{array}{lll} \int_0^\pi\cos^2x\sin x\, dx&=\int_0^\pi(\cos x)^2\sin x\, dx\\ &=\int_1^{-1} (u)^2\sin x\, \frac{du}{-\sin x}\\ &=\int_1^{-1} (u)^2\, \frac{du}{-1}\\ &=-\int_1^{-1} u^2\, du\\ &=\int_{-1}^{1} u^2\, du\\ &=\frac{1}{3}u^3\bigg|_{u=-1}^{u=1}\\ &=\frac{1}{3}\big( 1^3-(-1)^2 \big)\\ &=\frac{2}{3}. \end{array}$$ $\square$

This is what happens to integration by substitution when we proceed to definite integration. The extra step is the Fundamental Theorem of Calculus, for either variable: $$\newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccccccccc} & f(g(x))g'(x) &\ra{\int\, .. \, dx} & F(g(x)) &\ra{\text{ FTC }} & I&\\ \small\text{substitution }&\quad \ua{\text{CR}} & &\ \ \da{u=g(x)} && || &\small\text{ same!} \\ & f(u) &\ra{\int\, .. \, du} & F(u) &\ra{\text{ FTC }} & I& \end{array}$$ Thus, the result of definite integration -- a number -- is the same no matter what variable we choose.

Exercise. Execute the substitution $u=e^x$ for the integral (don't evaluate the resulting integral): $$\int_1^2 \cos (1-e^x)\, dx.$$

Trigonometric substitutions

Back to indefinite integrals...

Which substitution to choose might not be always obvious and when it is, it might lead to an integral that isn't any simpler that the original. The latter problem is especially common. Consider the familiar integral: $$\begin{array}{rrcll} ??? & & ??? & & \frac{1}{2}\int e^u\, du \\ & \nwarrow\ _{u=e^x} & \uparrow & _{u=x^2}\nearrow\\ ??? & \leftarrow\small{u=\sin x} & \begin{array}{|c|}\hline \quad \int xe^{x^2}\, dx \quad \\ \hline\end{array} & \small{u=x^3}\to & \frac{1}{3}\int u^{-1/3} e^{u^{2/3}}\, du\\ & \swarrow^{u=\cos x} & \downarrow & ^{u=x^4}\searrow\\ ??? & & ??? & & \frac{1}{4}\int u^{-1/2} e^{u^{1/2}}\, du\\ \end{array}$$ Even though the change of variables has been carries out correctly, it might still be a dead end!

Exercise. Carry out these substitutions.

Sometimes we have to come up with entirely new ideas...

Let's revisit the question addressed in the last chapter, what is the area of a circle of radius $R$? $$\text{Area }=2\int_{-R}^R \sqrt{R^2-x^2}\, dx=\pi R^2.$$

To prove the formula, we need integrate this: $$\int \sqrt{R^2-x^2}\, dx.$$ How?

There is a composition... Let's try substitution! The obvious choice is: $$u=R^2-x^2\ \Longrightarrow\ du=-2x\, dx.$$ Substitute: $$\int \sqrt{R^2-x^2}\, dx=\int\sqrt{u}\,\frac{du}{-2x}=\int\sqrt{u}\,\frac{du}{-2\sqrt{R^2-u}}=-\frac{1}{2}\int\sqrt{\frac{u}{R^2-u}}\,du.$$ Change of variables is completed but, unfortunately, the new integral is no simpler than the original!

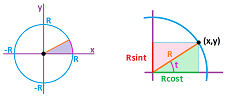
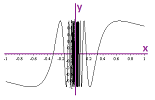
Let's take another look at the integrand: $$y=\sqrt{R^2-x^2}.$$ What is this? A circle of radius $R$. More precisely, its upper half is given directly (explicitly) as the graph of this function. The circle is also given by a relation (implicitly) by: $$x^2+y^2=R^2.$$ There may be a third possibility, if we just find a better variable...

On left, we interpret the graph representation of the circle visualized as motion: time on the $x$-axis and location on the $y$-axis. As a result, the dots appear at equal intervals of time, i.e., horizontally:

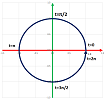
What we can see is how motion starts fast, then slows down to almost zero in the middle, and then accelerates again. But what if we consider instead a simple rotation on the plane? Such a rotation would progress through the angles at a constant rate, shown on right. So, maybe the angle, say $t$, should be our new variable? Then, the formulas for $x$ and $y$ come from the basic trigonometry: $$\begin{array}{ll} x=R\cos t,\\ y=R\sin t. \end{array}$$

The rotation is counterclockwise starting from $(R,0)$ and $t$ runs from $0$ to $\pi$.

A new variable has appeared naturally: $$x=R\cos t.$$ This is our substitution. Then main difference from previous examples of integration by substitution is that here, vice versa, the new variable is given in terms of the old. This is why such a formula is often called an inverse substitution. No matter! We have: $$t=\cos^{-1}(x/R),$$ with $$-\pi/2\le t\le \pi/2.$$ In fact, to carry out this change of variables all we need is this: $$dx=-R\sin t \, dt.$$ We substitute but, in order to simplify, we'll also need the Pythagorean Theorem: $$\sin^2t+\cos^2t=1.$$ Then, we find an antiderivative with respect to $t$ as follows: $$\begin{array}{lll} \int \sqrt{R^2-x^2}\, dx&=\int \sqrt{R^2-\cos^2t}\cdot (-R\sin t \, dt)&\text{...use PT}\\ &=\int R\sin t\cdot (-R\sin t \, dt)&\text{...change of variables finished}\\ &=-R^2\int \sin^2 t\, dt&\text{...a trig formula next}\\ &=-R^2\int \frac{1-\cos 2t}{2}\, dt&\\ &=-\frac{R^2}{2}\left( \int dt-\int\cos 2t\, dt\right)&\\ &=-\frac{R^2}{2}\left( t-\frac{1}{2}\sin 2t\right).\\ \end{array}$$ Integration is finished.

We won't do back-substitution because our interest is a definite integral. We only need to know the bounds for the new variable.

We find them from the picture, or from algebra: $$x=-R\ \Longrightarrow\ t=\pi\ \text{ and }\ x=R\ \Longrightarrow\ t=0.$$ Substitute: $$\begin{array}{lll} \text{area of a circle of radius } R\ &=2\cdot\int_{x=-R}^{x=R} \sqrt{R^2-x^2}\, dx\\ &=-2\cdot \frac{R^2}{2}\left( t-\frac{1}{2}\sin 2t \right)\Bigg|_{t=\pi}^{t=0}\\ &=-R^2\left( 0-\frac{1}{2}\sin (2\cdot 0) - (\pi+\frac{1}{2}\sin 2\pi \right)\\ &=\pi R^2. \end{array}$$

Exercise. Modify the proof for the substitution $x=R\sin t$.

Example. Recall how we evaluated the integral: $$\int x^2e^{x^2}\, dx=?$$ The substitution was chosen to be $u=x^2$ from which we derived the other two items: $$\begin{array}{lll} 1.&x^2&=u\\ 2.&dx&=\frac{du}{2x}\\ 3.&x&=\sqrt{u} \end{array}\quad \longrightarrow\quad \begin{array}{lll} 1.&x&=\sqrt{u}\\ 2.&dx&=\frac{du}{2\sqrt{u}}\\ 3.&x^2&=u \end{array}$$ However, we could have started with #3 (the inverse) with the same result! $\square$

Trigonometric Substitutions: For $a>0$,

• 1. when the integrand contains $\sqrt{a^2-x^2}$, or sometimes $a^2-x^2$, use substitution $x=a\cos t$ (or $x=a\sin t$);
• 2. when the integrand contains $\sqrt{a^2+x^2}$, or sometimes $a^2+x^2$, use substitution $x=a\tan t$;
• 3. when the integrand contains $\sqrt{x^2-a^2}$ (note the sign), or sometimes $x^2-a^2$, use substitution $x=a\sec t$.

Warning: this is not a theorem and it doesn't guarantee success.

Example. Let's simplify this: $$\int (4-x^3)^{3/2}\, dx.$$ The expression matches option (1): $$\begin{array}{ll} &a^2&-&x^2\\ &4&-&x^3\\ \Longrightarrow&a=2 \end{array}$$ Therefore, we try: $$x=2\cos x.$$

$\square$

Exercise. Use option (1) to evaluate this integral: $$\int \frac{1}{1+x^2}\, dx.$$

Exercise. Evaluate this integral: $$\int \sqrt{x^2-1}\, dx.$$

Integration by parts: products

The Product Rule for derivatives expresses the derivative of the product of two functions in terms of their derivatives (and the functions themselves): $$\left( f\cdot g\right)'=f'\cdot g+f\cdot g'.$$ There is no “Product Rule for integrals” that would express the integral of the product of two functions in terms of their integrals (and the functions themselves): $$\int\left( f\cdot g\right)\, dx=?$$

Let's nonetheless try to get whatever we can from PR. We integrate it: $$\begin{array}{lll} \int\left( f\cdot g\right)'\, dx &=\int\left( f'\cdot g+f\cdot g'\right)\, dx&\text{ we use FTC...}\\ f\cdot g &=\int\left( f'\cdot g+f\cdot g'\right)\, dx\\ &=\int f'\cdot g \,dx +\int f\cdot g'\,dx.\\ \end{array}$$ Now, these two integrals are very similar and either of them may be seen as the integral of a certain product. We derive something useful from this.

Theorem (Integration by Parts). For two integrable functions $f$ and $g$, we have $$\int f\cdot g' \,dx= f\cdot g -\int f'\cdot g\,dx.$$

We can also use the substitution formula, $$dh=h'(x)\, dx,$$ To obtain a more compact version.

Corollary (Integration by Parts). For two integrable functions $f$ and $g$, we have $$\int f\, dg= fg -\int g\, df.$$

The formula is traditionally restated with these, changed, names of the functions: $$\int udv= uv -\int vdu.$$

When we are to decide which technique of integration to use, we recognize that for integration by part we have to see in the integrand:

• a multiplication, but
• no composition.

Then, the approach won't work for $$\int xe^{x^2}\, dx$$ (we use substitution for that), nor for $$\int e^{x^2}\, dx$$ (we look it up). The approach might work for $$\int xe^x\, dx.$$

Example. If we are to integrate this, we need to match it with the integral in the formula. These two must be equal: $$\begin{array}{ll} \int u\, dv\\ \int x\cdot e^x\, dx. \end{array}$$ Unfortunately, there are at least two ways to match them:

• (a) $u=e^x,\quad dv=x\, dx$, and
• (b) $u=x,\quad dv=e^x\, dx$.

We'll have to do both.

(a) To use the formula, we need the derivative of $u$ and the integral of $v$: $$\begin{array}{ll} u=e^x & \Longrightarrow & du=e^x\, dx;\\ dv=x\, dx & \Longrightarrow & v=\int x\, dx=\frac{x^2}{2}. \end{array}$$ Integrating to find $v$ is the first part of integration. The second part is the one in the formula: $$\int udv= uv -\int vdu=e^x\cdot \frac{x^2}{2}- \int \frac{x^2}{2}\cdot e^x\, dx.$$ Unfortunately, we discover that the new integral looks even complex than the original! Indeed, the power of $x$ went up... Before attempting other techniques let's try to reverse the choice of $u$ and $v$.

(b) Once again, we need the derivative of $u$ and the integral of $v$: $$\begin{array}{ll} u=x & \Longrightarrow & du=dx;\\ dv=e^x\, dx & \Longrightarrow & v=\int e^x\, dx=e^x. \end{array}$$ We substitute these into the formula: $$\int udv= uv -\int vdu=x\cdot e^x- \int e^x\, dx.$$ We pause here to stop and appreciate the fact that the new integral is so less complex than the original! That's because the power of $x$ went down... We finish the computation: $$\int xe^x\, dx=x\cdot e^x- \int e^x\, dx=xe^x- e^x+C.$$ $\square$

The lesson seems to be:

• choose for $u$ the part of the integrand that will be simplified by differentiation, and
• choose for $dv$ the part of the integrand that will be simplified by integration,

or at least will remain as simple.

Example. Integrate: $$\int x^2e^x\, dx.$$ Once again, there are (at least) two ways to choose $u$ and $dv$:

• (a) $u=e^x,\quad dv=x^2\, dx$, and
• (b) $u=x^2,\quad dv=e^x\, dx$.

We'll try both.

(a) We find the derivative of $u$ and the integral of $v$: $$\begin{array}{ll} u=e^x & \Longrightarrow & du=e^x\, dx;\\ dv=x^2\, dx & \Longrightarrow & v=\int x^2\, dx=\frac{x^3}{3}. \end{array}$$ Even though $du$ is just as simple as $u$, integration of $dv$ has made things worse. Indeed, we have: $$\int udv= uv -\int vdu=e^x\cdot \frac{x^3}{3}- \int \frac{x^3}{3}\cdot e^x\, dx.$$ It's not simpler as the power of $x$ goes up! We reverse the choice of $u$ and $v$.

(b) The derivative of $u$ and the integral of $v$: $$\begin{array}{ll} u=x^2 & \Longrightarrow & du=2x\,dx;\\ dv=e^x\, dx & \Longrightarrow & v=\int e^x\, dx=e^x. \end{array}$$ Here $dv$ is simpler than $u$; that's a good sign. We substitute these into the formula: $$\int udv= uv -\int vdu=x^2\cdot e^x- \int e^x\cdot 2x\, dx.$$ Again, we pause to appreciate the fact that the integration task has been simplified! That's because the power of $x$ went down... We finish the computation using the integration by part formula and the result of the last example: $$\int x^2e^x\, dx=x^2\cdot e^x- \int e^x2x\, dx=x^2e^x- 2xe^x+ 2e^x+C.$$ $\square$

The lesson is that integration by parts might bring simplification of the integral and might require another application of integration by parts.

Exercise. Apply the formula found in this example to the previous example, part (a).

Exercise. In the last example, try this decomposition of the integrand: $u=x, \ dv=xe^x$.

Example. Integrate: $$\int x^3\sin x\, dx.$$ There are two ways to split the integrand, $u$ and $dv$, but we already know that integration by part will reduce the power $x$ -- if we choose $u=x^3$. we are left with $dv=\sin x$. Then $$\begin{array}{ll} u=x^3 & \Longrightarrow & du=3x^2\,dx;\\ dv=\sin x\, dx & \Longrightarrow & v=\int \sin x\, dx=-\cos x. \end{array}$$ By parts: $$\int x^3\sin x\, dx= uv -\int vdu=-x^3\cos x- \int 3x^2\cdot \sin x\, dx.$$ The last integral is almost identical to the original but the power of $x$ is down by $1$. $\square$

Exercise. Finish the computation by integrating by parts two more times.

Example. Integrate: $$\int \cos ^{-1}x\, dx.$$ There seems to be nothing to split in the integrand!.. There is: $$\begin{array}{lll} u=\cos ^{-1}x & \Longrightarrow & du=-\frac{1}{\sqrt{1-x^2}}\,dx;\\ dv=dx & \Longrightarrow & v=\int \, dx=x. \end{array}$$ By parts: $$\begin{array}{lll} \int \cos ^{-1}x\, dx&= uv -\int vdu\\ &=\cos ^{-1}x\cdot x- \int x\left( -\frac{1}{\sqrt{1-x^2}} \right)\, dx&\text{...done with parts}\\ &=x\cos ^{-1}x+ \int \frac{x}{\sqrt{1-x^2}}\, dx&\text{...by substitution: }&\quad z=1-x^2\\ &=x\cos ^{-1}x+ \int \frac{1}{\sqrt{z}}\, \frac{dz}{-2}&& \Rightarrow dz=-2xdx\\ &=x\cos ^{-1}x-\frac{1}{2} z^{-1/2}\, dz\\ &=x\cos ^{-1}x-\frac{1}{2} \frac{z^{1/2}}{1/2}+C&\text{...back-substitution}\\ &=x\cos ^{-1}x-\sqrt{1-x^2}+C.\\ \end{array}$$ $\square$

Exercise. Apply the Integration by Parts formula to the integral, $$\int xe^x\, dx,$$ with these two choices of the “parts”:

• (a) $x$ and $e^x\, dx$,
• (b) $e^x$ and $x\, dx$.

Approaches to integration

Let's summarize what we know about integration and compare it to what we know about differentiation.

First, the similarities.

Just as there is a list of elementary derivatives, a list of elementary integrals. In fact, the latter comes from the former.

Integral formulas for specific functions. On any interval within the domain, we have: $$\begin{array}{lll} \int e^{x} \, dx &= e^{x} + C; \\ \int \sin x \, dx &= -\cos x + C; \\ \int \cos x \, dx &= \sin x + C; \\ \int x^{s} \, dx &= \frac{x^{s+1}}{s+1} + C, \, \text{ provided } s \neq -1;\\ \int \frac{1}{x} \, dx &= \ln |x| + C . \end{array}$$

So, given a function, we find it on the list and here is its integral, just like with the derivatives. And, in either case, the list is very short!

There are differences already between the two. The presence of “$+C$” in each integral indicates that the answer contains infinitely many functions. Also, the formulas for integrals only remain valid when limited to intervals.

Just as there are algebraic rules of differentiation, there are algebraic rules of integration. The latter comes, in part, from the former.

Rules of integrals:

• Sum Rule:

$$\int (f+g)\, dx=\int f\, dx+\int g\, dx;$$

• Constant Multiple Rule:

$$\int (cf)\, dx=c\int f\, dx.$$

The way we apply the two rules is very similar to the one for derivatives:

• when the function to be integrated is the sum of two (just as when it was to be differentiated), we split the integral into two and then deal with either (simpler) integral separately;
• when the function to be integrated is a constant multiple of another (just as when it was to be differentiated), we factor it out and then deal with the remaining (simpler) integral.

The similarities stop here!

What about the Product Rule for integration? There is none in the above sense:

• when the function to be integrated is the product of two (unlike when it was to be differentiated), we can't split the integral into two and then deal with either integral separately.

The reason is that the Product Rule for differentiation can't be easily reversed... unless one of the functions is, in fact, the derivative of a function that we know or can find. That's the Integration by Parts formula: $$\int fg'\,dx=fg-\int gf'\,dx.$$

And what about the Quotient Rule for integration? There is none, unless you are willing to interpret division as multiplication by the reciprocal...

Now, what about the Chain Rule? Same problem as with the products:

• when the function to be integrated is the composition of two (unlike when it was to be differentiated), we can't split the integral into two and then deal with either integral separately.

The reason is that the Chain Rule for differentiation can't be easily reversed... unless the derivative of the function on the inside is, in fact, present as a factor. That's the Integration by Substitution formula: $$\int (f\circ g)\cdot g'\,dx=\int f\,du.$$ The Chain Rule for differentiation is also easily reversed when the function on the inside is linear. That's the Linear Composition Rule: $$\int f(mx+b)\, dx=\tfrac{1}{m}\int f(t)\, dt\Big|_{t=mx+b},$$ provided $m\ne 0$.

Example. Compute: $$\int_{0}^{1} \left( x^{3} + 3e^{x} - \sin x \right) \, dx.$$ Ignore the bounds at first: $$\begin{array}{rcl} \int \left( x^{3} + 3e^{x} - \sin x \right) \, dx & \overset{\text{SR}}{=\! =\! =\! =\! =} &\int x^{3} \, dx + \int 3e^{x} \, dx + \int \sin x \, dx \\ & \overset{\text{CMR}}{=\! =\! =\! =\! =} &\int x^{3} \, dx + 3 \int e^{x} \, dx + \int \sin x \, dx \\ & \overset{\text{formulas}}{=\! =\! =\! =\! =}& \frac{x^{4}}{4} + 3\cdot e^{x} - \left( -\cos x \right) + C \\ & \overset{\text{simplify}}{=\! =\! =\! =\! =}& \frac{1}{4}x^{4} + 3e^{x} + \cos x + C. \end{array}$$ That's the hard part, finding antiderivatives. Now the easy part: $$\begin{array}{rcl} \int_{0}^{1} \left( x^{3} + 3e^{x} - \sin x \right) \, dx & \overset{\text{FTC}}{=\! =\! =\! =\! =} &\left. \frac{1}{4} \, x^{4} + 3e^{x} + \cos x \right|_{0}^{1} \\ & \overset{\text{substitute}}{=\! =\! =\! =\! =}& \left( \frac{1}{4} \, 1^{4} + 3e^{1} + \cos 1 \right) + \left( \frac{1}{4} \, 0^{4} + 3e^{0} + \cos 0 \right) \\ &= &\frac{1}{4} + 3e + \cos 1 - 0 - 3 -1. \end{array}$$ The hard part is easy when there is no multiplication, division, or composition of functions. $\square$

Warning: The most important approach to integration is using the table of integrals!

The main difference is that differentiation never fails but integration may fail in the sense that the integral might turn out to be a function we have never seen before or even a function that no-one has seen before!

To see what happens recall how we created a new function, the Gauss error function, as the integral: $$\operatorname{erf}(x)=\frac{2}{\sqrt{\pi}}\int e^{-x^2}\, dx.$$ There are many more examples of those and even if we keep adding these new functions to the list of “familiar” functions, there will always remain integrals not on the list...

We can use the same approach to re-discover “familiar” function -- starting at the other end. For example, integrating this rational function produces the logarithm: $$\frac{1}{t}\ \leadsto\ \int _1^x \frac{1}{t}\, dt=\ln x.$$ We have defined the logarithm without reference to the inverse of the exponential function. Also, integrating this algebraic function produces the arcsine: $$\frac{1}{\sqrt{1-t^2}}\ \leadsto\ \int_0^x \frac{1}{\sqrt{1-t^2}}\, dt=\sin^{-1}x.$$ We have defined the arcsine without reference to the inverse of the sine.

The areas of infinite regions: improper integrals

We can only integrate over closed and bounded intervals such as $[a,b]$.

Example. Consider this seemingly familiar formula: $$\int \frac{1}{x} \, dx \ \overset{\text{???}}{=\! =\! =\! =}\ \ln |x| + C,\ x \ne 0.$$ The formula is false as stated! It holds only on either of the two intervals, separately, of the domain of $\frac{1}{x}$, i.e., $(-\infty,0)$ and $(0,\infty)$, but not on the set $(-\infty,0)\cup(0,\infty)$. This means that $C$ can vary from the one to the other! For example, this is an antiderivative: $$F(x) = \begin{cases} \ln |x| + C & \text{ for } x < 0, \\ \ln |x| + K & \text{ for } x > 0. \end{cases}$$ It is even more dangerous to ignore the gap in the domain when we deal with definite integrals. For example, one might have this: $$\int_{-1}^1 \frac{1}{x} \, dx \ \overset{\text{???}}{=\! =\! =\! =}\ \ln |x| \Bigg|_{-1}^1 = \ln 1-\ln |-1|=0.$$ Best, we can tell, the integral is indeterminate! Indeed, $f$ is not integrable on $[-1,1]$ simply because it's undefined at $x=0$. Furthermore, even though the positive and the negative areas seem to cancel each other, this is false because both are, in fact, infinite...

...and shouldn't think that $$\infty-\infty\ \overset{\text{???}}{=\! =\! =\! =}\ 0.$$ $\square$

Exercise. Show that the function in the example won't become integrable whatever number we assign to $x=0$.

We will next try to understand the meaning of the area of an infinite or, better, unbounded region.

Example (infinite bottle). The area of this “infinite rectangle”, like the one below, must be infinite:

Why or in what sense? This region contains a growing sequence of (finite) rectangles the areas of which grow to infinity. In other words, it would take an infinite amount of water to fill such a bottle. $\square$

We have come to understand the meaning of the areas of (some) bounded regions. It, then, will be our approach to “exhaust” an unbounded region with a sequence of bounded regions, find their areas, and then examine the limit of these areas.

We will restrict our attention to regions

• unbounded with respect to the $x$-axis (infinitely wide), and
• unbounded with respect to the $y$-axis (infinitely tall).

As we only deal with regions determined by graphs of functions, the former case is about functions with unbounded domains or, better, unbounded domains of integration and the latter about functions with unbounded ranges (i.e., unbounded functions).

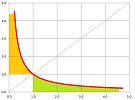
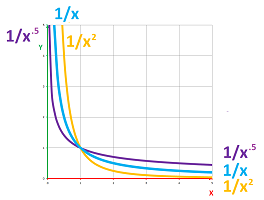
Even though these two classes of functions are very different, the issue is the same. For example, $y=1/x$ defines two identical unbounded regions:

We start with the former case: an unbounded domain of integration.

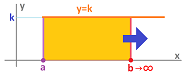
Example. Consider a constant function, $$f(x)=k \text{ on } [a,\infty),\ k>0.$$ Then, the area of the region above the interval $[a,b]$ with $b>a$ (and the integral from $a$ to $b$) is equal to $(b-a)k$. Furthermore, $$\text{Area }=(b-a)k\ \to +\infty\ \text{ as }\ b\to +\infty.$$

Therefore, the area of the infinite strip is infinite, as expected. $\square$

Initially, we will concentrate on rays as domains: $$(-\infty, b] \text{ and } [a,+\infty).$$ The rays will have to be “exhausted” with closed and bounded intervals because those are the only ones that we can handle as Riemann integrals.

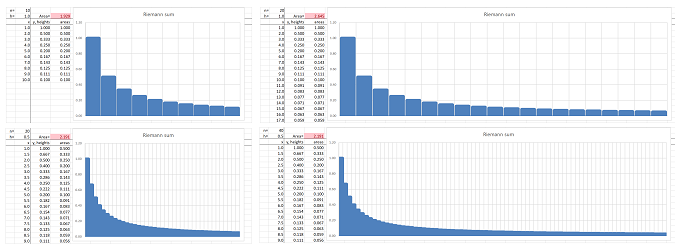
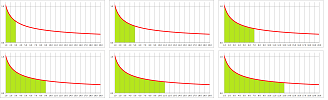
Example. Consider again $$f(x)=1/x \text{ on } [1,\infty).$$ Then the area under this graph over this ray in the $x$-axis is shown above.

This unbounded region is exhausted by bounded ones. How? The obvious approach is to use the Riemann sums. The challenge is that one has to both make the rectangles thinner and thinner (as before) and make the right end of the interval extend more and more to the right.

(Note that when $h=1$, this sum is called a series to be discussed in Chapter 15.)

An alternative approach is to rely on what we already know about areas under the graphs when the interval is bounded. The underlying ray of this region is exhausted with bounded intervals. They all have the same left bound, $1$, but the right bound, $b$, is approaching infinity: $$[1,b]\ \leadsto \ [1,+\infty)\ \text{ as } b\to +\infty .$$ Then, $$\begin{array}{ll} \int_1^b \frac{1}{x}\, dx&=\ln b-\ln 1 \\ &\to\infty &\text{ as } b\to +\infty. \end{array}$$ The area of the unbounded region is infinite. $\square$

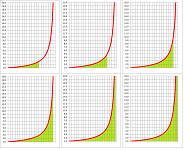
Example. So, the band under the graph of $f(x)=1/x$ is narrowing down but not fast enough to avoid growing its area to infinity. Let's try, in contrast, a function that would give us a narrower strip. How about $g(x)=1/x^2$? We have: $$\begin{array}{ll} \int_1^b \frac{1}{x^2}\, dx&=-\frac{1}{b}+1 \\ &\to 1 &\text{ as } b\to +\infty . \end{array}$$ So, $1$ is the area of the unbounded region. It's finite! $\square$

Example. What function decreases faster than all $1/x^n,\ n=1,2,3,...$? It's the exponential decay function: $$f(x)=e^{-x} \text{ on } [1,\infty).$$ Again, the unbounded region under this graph above this ray is exhausted by exhausting the underlying ray with the bounded intervals: $$[1,b]\ \leadsto \ [1,+\infty)\text{ as } b\to +\infty .$$

Then, $$\begin{array}{lll} \text{total area }&=\lim_{b\to +\infty} \int_1^b e^{-x}\, dx\\ &=\lim_{b\to +\infty}(-e^{-b}-(-e^{-1}))\\ &=\frac{1}{e} . \end{array}$$ $\square$

The main discovery is that the area of an unbounded region may be finite!

Exercise. Find the area under the graphs of (a) $y=\frac{1}{x^2}$, and (b) $y=\frac{1}{\sqrt{x}}$, over $[1,\infty)$.

Example. What if the function isn't all positive? What is the area -- over the positive numbers -- under a sinusoid?

The analysis is identical: $$\text{total area }=\lim_{b\to +\infty} \int_0^b \cos x\, dx=\lim_{b\to +\infty}(\sin b - \sin 0)\quad \text{...DNE }.$$ The limit doesn't exit and, therefore, there is no area. $\square$

Just as with all limits, there are three possible outcomes: this may be a number, or it may be infinite, or it may be undefined.

This is the summary. We “exhaust” the unbounded domain of integration, $(-\infty,b]$ or $[a,\infty)$, with bounded ones. If the function is integrable on these closed and bounded domains, we then “exhaust” a possibly infinite area of over this domain with finite ones. If the limits of these integrals exists, it is denoted by: $$\int_{-\infty}^b f(t) \, dt=\lim_{a \to -\infty} \int_a^b f(t) \, dt,$$ and $$\int_a^\infty f(t) \, dt=\lim_{b \to +\infty} \int_a^b f(t) \, dt .$$ These limits can also be infinite.

Warning: Even though the notation suggests that the domain of integration is the whole ray, this is nothing but an abbreviation for the limit on the right.

We also define the integral over the whole real line $(-\infty,\infty)$ in terms of the ones over rays, as the sum of two corresponding integrals (limits) with the following notation: $$\int_{-\infty}^\infty f(t) \, dt=\int_{-\infty}^0 f(t) \, dt+\int_0^\infty f(t) \, dt.$$

In the case of infinite limits, we utilize the algebra of infinities as shortcuts: $$\begin{array}{llll} (\text{ number }) + (+\infty)&=+\infty,\\ (\text{ number }) + (-\infty)&=-\infty\\ (+\infty) + (+\infty)&=+\infty,\\ (-\infty) + (-\infty)&=-\infty. \end{array}$$

Example. Let's compute the integral, $$\int_{-\infty}^{+\infty}e^x\, dx=...$$

$\square$

Definition. The limits of the integrals above are called improper integrals. When such a limit exists, or the two limits in the last case exist, we say that the improper integral converges and the function is integrable, otherwise it diverges.

Exercise. Show that replacing $0$ in the definition of the integral over $(-\infty,+\infty)$ with any real $c$ will produce the same result.

Exercise. Show that replacing the last definition with $$\int_{-\infty}^\infty f(t) \, dt\ \overset{\text{???}}{=\! =\! =\! =}\ \lim_{R\to \infty}\int_{-R}^R f(t) \, dt,$$ won't always produce the same result.

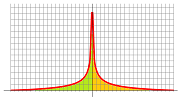
Example. The definition of the integral over $(-\infty,\infty)$ follows the additivity of the integral that comes from the idea of additivity of the areas. For example, this is what such an integral looks like:

The function is $e^{-x^2}$ and the integral is known to be convergent. $\square$

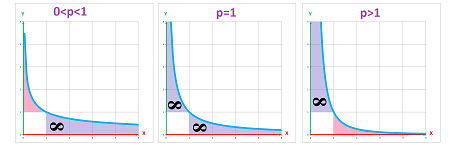
Theorem (Integrals of Reciprocals). For any $a>0$, we have $$\int_a^\infty \frac{1}{x^p}\, dx= \begin{cases} \frac{a^{1-p}}{p-1} &\text{ when } p>1,\\ \infty &\text{ when } 0<p\le 1. \end{cases}$$

Proof. For $p\ne 1$, we have: $$\begin{array}{lll} \int_a^\infty \frac{1}{x^p}\, dx&=\lim_{b\to\infty}\int_a^b \frac{1}{x^p}\, dx&\text{ ...by definition}\\ &=\lim_{b\to\infty}\int_a^b x^{-p}\, dx&\text{ ...use PF next}\\ &=\lim_{b\to\infty} \frac{1}{-p+1}x^{-p+1}\Bigg|_a^b\\ &=\frac{1}{-p+1}\lim_{b\to\infty} \left( b^{-p+1}-a^{-p+1} \right)\\ &=\frac{1}{-p+1}\left( \lim_{b\to\infty} b^{-p+1}-a^{-p+1} \right). \end{array}$$ The remaining limit is $0$ when $-p+1<0$ and it is infinite when $-p+1>0$. $\blacksquare$

Exercise. Finish the proof.

In other words, the integral

• converges when $p>1$,
• diverges when $0<p\le 1$.

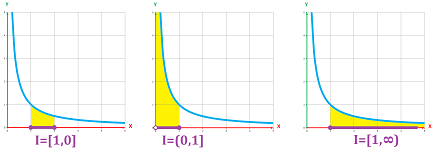
Now, the latter case: unbounded functions and bounded domains of integration.

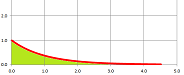
Example. Consider $$f(x)=\frac{1}{1-x} \text{ on } [0,1).$$ The area under this graph over this half-open interval in the $x$-axis is shown below:

How do we understand the area under this graph over this interval? We can use the Riemann sums, exactly as always, as long as it $1$ is not among its sample points!

Alternatively, this unbounded region is exhausted by bounded ones. How? The underlying interval of this region is by exhausted with closed intervals. They all have the same left bound, $a$, but the right bound, $b$, is approaching $1$: $$[0,b]\ \leadsto \ [0,1)\text{ as } b\to 1.$$ Then, $$\begin{array}{ll} \int_0^b \frac{1}{1-x}\, dx&= -\ln (1-b)-\ln 1 \\ & \to\infty &\text{ as } b\to 1 , \end{array}$$ which is then the area of the unbounded region. $\square$

The definition of the Riemann integral simply doesn't apply to a function undefined at one of the ends of the interval. Instead, we consider a restriction of the function to a smaller, but closed, interval.

Initially, we will concentrate on half-open intervals: $$(c, b] \text{ and } [a,c).$$

As you see, the analysis is very similar to the former case, with this substitution: $$[a,\infty)\ \longrightarrow\ [a,c).$$ Just as the former, the latter will have to be “exhausted” with closed and bounded intervals.

Example. Let's consider $$f(x)=\frac{1}{\sqrt{1-x}} \text{ on } [0,1).$$ Even though their graphs look almost identical, this one increases slower than the last one. Again, the unbounded region under this graph over this half-open interval is exhausted by exhausting the underlying ray with the closed intervals, $[0,b]$ as $b\to 1$. Then $$\begin{array}{ll} \text{unbounded area }&=\lim_{b\to 1} \int_0^b \frac{1}{\sqrt{1-x}}\, dx\\ &=\lim_{b\to 1}-2\sqrt{1-x}\Bigg|_{0}^b\\ &=2 . \end{array}$$ $\square$

The area of an unbounded region may be finite!

Example. What if the function isn't all positive? What is the area under an oscillating graph, such as $$y=\sin\frac{1}{x}?$$

With the graph like this, one can guess that the limit doesn't exist and, therefore, there is no area. $\square$

Just as with all limits, there are three possible outcomes for these areas: a number, infinity, or undefined.

This is the summary. We “exhaust” the half-open domain of integration, $(a,b]$ or $[a,b)$, with closed ones. If the function is integrable on these closed and bounded domains, we then “exhaust” a possibly infinite area over this domain with finite ones. If the limits of these integrals exists, it is denoted by: $$\int_{c}^b f(t) \, dt=\lim_{a \to c} \int_a^b f(t) \, dt,$$ and $$\int_a^c f(t) \, dt=\lim_{b \to c} \int_a^b f(t) \, dt .$$ These limits can also be infinite.

Warning: The notation is unfortunately identical to the one for proper integrals, but this is nothing but an abbreviation for the limit on the right.

We also define the integral over an open interval in terms of the ones over half-open intervals, with the following notation: $$\int_{a}^b f(t) \, dt=\int_{a}^c f(t) \, dt + \int_c^b f(t) \, dt,$$ for any $c$ between $a$ and $b$. In the case of infinite limits, we follow the algebra of infinities above.

Example. Let's compute the integral: $$\int_0^1\frac{1}{x(x-1)}\, dx=...$$

$\square$

We repeat the definition for the former case.

Definition. The limits of the integrals above are (also) called improper integrals. When the limit exists, or the two limits in the last case exist, we say that the improper integral converges and the function is integrable, otherwise it diverges.

Exercise. Show that replacing the last definition with $$\int_{a}^b f(t) \, dt\ \overset{\text{???}}{=\! =\! =\! =}\ \lim_{\varepsilon\to 0^+}\int_{a+\varepsilon}^{b-\varepsilon} f(t) \, dt.$$ won't produce the same result.

Example. The definition of the integral over an interval with a possible missing point inside follows additivity of the integral that comes from the idea of additivity of the areas. For example, this is what such an integral looks like:

The function is $\frac{1}{\sqrt{|x|}}$ and the integral is known to be convergent. $\square$

Theorem (Integrals of Reciprocals). For any $a>0$, we have $$\int_0^b \frac{1}{x^p}\, dx= \begin{cases} \frac{b^{1-p}}{1-p} &\text{ when } 0<p<1,\\ \infty &\text{ when } p\ge 1. \end{cases}$$

Proof. For $p\ne 1$, we have: $$\begin{array}{lll} \int_0^b \frac{1}{x^p}\, dx&=\lim_{a\to 0^+}\int_a^b \frac{1}{x^p}\, dx&\text{ ...by definition}\\ &=\lim_{a\to 0^+}\int_a^b x^{-p}\, dx&\text{ ...use PF next}\\ &=\lim_{a\to 0^+} \frac{1}{-p+1}x^{-p+1}\Bigg|_a^b\\ &=\frac{1}{-p+1}\lim_{a\to 0^+} \left( b^{-p+1}-a^{-p+1} \right)\\ &=\frac{1}{-p+1}\left( b^{-p+1}-\lim_{a\to 0^+}a^{-p+1} \right). \end{array}$$ The remaining limit is $0$ when $-p+1>0$ and it is infinite when $-p+1<0$. $\blacksquare$

Exercise. Finish the proof.

Exercise. Match the integrals and the areas of the two theorems about integrals of the reciprocals. Hint: it's about symmetry.

In other words, the integral $\int_0^b \frac{1}{x^p}\, dx$:

• converges when $p>1$,
• diverges when $0<p\le 1$.

This is the summary of the two types of improper integrals for these functions:

Exercise. What possible values can the area between the graph of a function and its asymptote take? Give an example for each value.

Example. In addition to the areas, improper integrals can also be explained in terms of motion. If our velocity is positive but declining as $1/x^2$, where $x$ is time, the distance we will cover over an infinite period of time will not be infinite! $\square$

Properties of proper and improper definite integrals

Thus, we have extended the idea of Riemann integral with the domain of integration:

• closed bounded intervals, such as $[a,b]$, to
• half-open, such as $(a,b]$ and $[a,b)$, and also possibly infinite, such as $(-\infty,b]$ and $[a,\infty)$, and further to
• open intervals, such as $(a,b)$, and possibly infinite, such as $(-\infty,+\infty)$.

If we denote an interval by $I$, all these integrals can be written in the same notation: $$\int_I f\, dx.$$

Let's take a more general view. We consider integrals over an arbitrary interval $I$.

These integrals have identical properties. In fact, the properties of improper integrals follow from the corresponding properties of proper integrals (which in turn come from the properties of limits).

As regions are joined together via union, their areas are added -- even though the regions may be unbounded. The area interpretation of additivity is the same as before, as long as the integrals are convergent:

Theorem (Additivity). Suppose $f$ is integrable over intervals $I$ and $J$ that share at most one point. If $I\cup J$ is an interval then $f$ is integrable over $I\cup J$ and we have: $$\int_I f\, dx +\int_J f\, dx = \int_{I\cup J} f\, dx.$$

Theorem. If $f$ is integrable over interval $I$ then it is also integrable over any interval $J\subset I$.

The algebraic rules are the same.

Theorem (Sum Rule). Suppose $f$ and $g$ are integrable functions over interval $I$. Then so is $f+g$ and we have: $$\int_I \left( f + g \right)\, dx = \int_I f\, dx + \int_I g\, dx. $$

Theorem (Constant Multiple Rule). Suppose $f$ is an integrable function over interval $I$. Then so is $c\cdot f$ for any real $c$ and we have: $$ \int_I (c\cdot f)\, dx = c \cdot \int_I f\, dx.$$

Exercise. Prove the two theorems. Hint: use the rules of limits.

Exercise. What is the Fundamental Theorem of Calculus for improper integrals?

The following is a major theorem from Chapter 5.

Theorem. Every monotone bounded sequence converges.

Since the convergence of the antiderivative of a function is what determines the convergence of its definite integral, we look at its behavior, we realize that it is monotone when the function is either all positive or all negative. This way, we exclude functions with a different kind of divergence of its integral, such as $\sin$ and $\cos$:

Then, we have the following.

Theorem (Convergence). If a function is non-negative, its integrals are either convergent or infinite.

Exercise. Prove the theorem.

Then, to establish convergence we can use a direct comparison with another function, a function that has a convergent integral. Similarly, to establish divergence, we can use a direct comparison with another function, a function that has a divergent integral.

Example. Consider these two facts:

• the integral $\int_1^\infty\frac{1}{x^{1/2}}\, dx$ diverges because $\int_1^\infty\frac{1}{x^{1/3}}\, dx$ does, and
• the integral $\int_1^\infty\frac{1}{x^{3}}\, dx$ converges because $\int_1^\infty\frac{1}{x^2}\, dx$ does.

We draw these conclusions from these inequalities: $$\begin{array}{ccccccc} 1/3&\le 1/2&\le &2&\le 3 &\Longrightarrow\\ x^{1/3}&\le x^{1/2}&\le &x^2&\le x^3&\Longrightarrow\\ \frac{1}{x^{1/3}}&\ge\frac{1}{x^{1/2}}&\ge&\frac{1}{x^2}&\ge\frac{1}{x^3}&\Longrightarrow\\ \int_1^\infty\frac{1}{x^{1/3}}\, dx&\ge\int_1^\infty\frac{1}{x^{1/2}}\, dx&=\infty>&\int_1^\infty\frac{1}{x^2}\, dx&\ge\int_1^\infty\frac{1}{x^3}\, dx. \end{array}$$ $\square$

Exercise. What does the middle inequality give us?

The idea applies to all improper integrals.

Theorem (Comparison). Suppose $I$ is an interval, and $$0\le f(x)\le g(x)$$ for all $x$ in $I$. Then, for improper integrals over $I$, we have:

• (a) if the improper integral of $f$ diverges then so does the improper integral of $g$;
• (b) if the improper integral of $g$ converges then so does the improper integral of $f$ and

$$0\le \int_I f \, dx \le \int_I g \, dx.$$

Exercise. Prove the theorem.

Suppose the functions are non-negative. According to the Convergence Theorem, the following notation makes sense:

• when the integral diverges, we write:

$$\int_I f\, dx=\infty;$$

• when the integral converges, we write:

$$\int_If\, dx<\infty.$$

Then the Comparison Theorem above can be read from these simple inequalities: $$\int_I f\, dx\ge \int_I g\, dx=\infty;$$ and $$\int_I f\, dx\le \int_I g\, dx<\infty.$$

Exercise. What if we use strict inequalities in the above example?

Exercise. What can we derive about the convergence/divergence of the improper integrals of the reciprocal powers based entirely on that of $1/x$. Hint:

Exercise. State and prove the Squeeze Theorem for improper integrals.