This site is being phased out.
Topology
Contents
Topology -- Algebra -- Geometry
In an attempt to capture the essence of topology in a single sentence, we usually say that topology is the science of spatial properties that are preserved under continuous transformations. To elaborate a bit: you can bend, stretch, and shrink but not tear or glue.
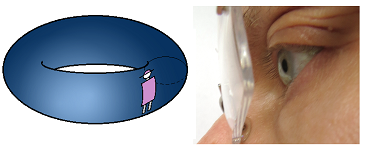
In order to illustrate this idea in context of mathematics as a whole, let's take a look at these delicious donuts:
In order to see how topology is necessary for counting, consider the fact that the first step is to recognize that these are separate objects - disconnected from each other! Furthermore, to count the holes, we need to recognize them as a different kind of topological feature. In fact, counting, computing, and measuring are all preceded by our ability to perceive the topology in these pictures.
As we shall see, topology is the science of spatial properties that don't rely on measuring.
Now, to answer “why do we need to study topology?”, we start with a few elementary examples. They come from four seemingly unrelated areas: vision and computer vision, cosmology, data analysis, and social choice theory.
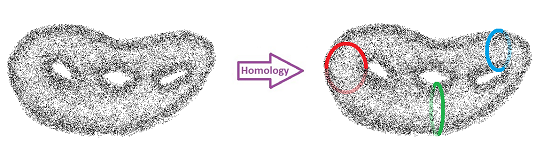
The integrity of everyday objects
In order to be able to delegate some of the decision making to computers, one has to start by describing what he intuitively understands, in absolutely unambiguous terms.
In industrial context, one might need to consider the integrity of objects being manufactured or inspected.
The first question may be: this bolt is supposed to hold two things together; is it still capable of that, or is there a crack in it?
In other words: would the bolt hold a hair or would the hair slip through?
The second question may be: this porous material is supposed to stop a flow of liquid; is it still water-tight or is there leakage?
In other words: would the sheet hold water or might some permeate through?
The third question may be: to be strong, this alloy is supposed to be solid; is it still solid, or are there air bubbles?
In other words: would the alloy hold no air, or might some get in?
It is important to understand now that these are three different kinds of integrity loss - as there may be a crack but no hole or vice versa, etc.:
We can describe the three situations informally as follows: The objects have:
- cuts, or
- tunnels, or
- voids.
Exercise. Sketch examples for all possible combinations of cuts, tunnels, and voids with one or none of each and indicate corresponding real-life objects.
Of course, the presence of one of these features doesn't have to mean that the object is defective, as in the examples: a rope, a bucket, and paint. The examples of objects that are intended to have such a topological feature are respectively: sliced bread, a strainer, and a balloon.
Next, we will classify these three types of “defects”, according to their dimensions.
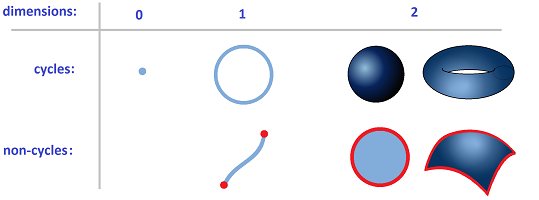
To understand why and how, let's recall from the elementary geometry (or linear algebra) the list $0$-dimensional, $1$-dimensional and $2$-dimensional spaces:
- 0. points,
- 1. lines,
- 2. planes.
If these spaces are allowed to be deformed, the list becomes:
- 0. points,
- 1. curves,
- 2. surfaces.
Some of those are special - in the sense that they have no end-points or edges, i.e., there are no boundaries, as in these:
- 0. point,
- 1. circle,
- 2. sphere.
These, as well as their deformed versions, are called cycles. Meanwhile, objects that have no such features are called acyclic.
Finally, our conclusions.
$\bullet$ 0. Any two points form a 0-cycle and, since this is the simplest example of a cut, the latter is a 0-dimensional feature:
$\bullet$ 1. Any circle is a 1-cycle and, since this is the simplest example of a tunnel, the latter is a 1-dimensional feature:
$\bullet$ 2. Any sphere is a 2-cycle and, since this is the simplest example of a void, the latter is a 2-dimensional feature:
Exercise. Using this terminology, describe the topology of: a basketball, a football, a cannonball, a doughnut, an inner tire, a steering wheel, a bicycle wheel, a potter's wheel, a fingerprint, a tree, an envelope.
Exercise. Suggest your own examples of topological issues in everyday life and describe them using this terminology.
What if we deform these objects as if they are made of rubber? We can stretch and shrink them and, as long as we do not cut or glue, the number of topological features will remain the same. Indeed, the cuts, holes, and voids may narrow but won't disappear. Indentations may appear but they won't turn into topological features.
This property is exemplified by an amoeba - a single-cell organism able to freely change its form.
Exercise. Sketch a sequence of steps to show how this man - let us first appoint him amoeba-like abilities - can unlock his hands while his fingers remain together and continue to form the two loops.
What about more general continuous transformations?
Breaking a bolt is not continuous but welding it back together is. Digging a tunnel (all the way) through a wall is not continuous but filling it shut is. Piercing a bubble is not continuous but patching it is. Bread is cut, tires are punctured, paper is folded into an origami, fabric is sewed into a suit or an airbag, etc., etc.
As these examples show that even continuous transformations can create and remove topological features.
Exercise. Describe what happens to the three topological features in the above examples.
Exercise. Describe, in precise terms, what happens to the amoeba's topology as it feeds? Indicate which stages of development are continuous and which aren't.
The shape of the Universe
What is the shape of the Universe? What is its topology? Does the Universe have “cuts”, “tunnels”, or “voids”?
Looking around, we don't observe any of these! But remember how, hundreds of years ago, sailors started to notice the curvature of the horizon? And later they proved - by around-the-world travel and even later by orbiting - that the surface of the Earth encloses something inside?
As for the Universe, what we know is that we are not living in the flat world of Euclid and Newton; we are living in the curved world of Riemann and Einstein:
But the Universe that curves and bends here might curve and bend everywhere! Then, no matter how small the bend is, it might close on itself:
It may be possible then to travel in a straight line and arrive at the starting point from the opposite direction. In fact, the light of the Sun may come to us from an unexpected direction and, as a result, appear to come from a distant star:
Events of this kind would provide us with clues about the topology of the Universe. We have to rely on such indirect observations because we can't step outside and observe the Universe from there:
Since we have to stay inside our Universe, we can't see its “cuts”, “tunnels”, or “voids”. The only way we can discover its structure is by traveling or by observing others - such as light or radio waves - travel.
If multiple universes exist but we have no way of traveling there, we can't confirm their existence. So much of $0$-cycles...
Traveling in various directions and coming (or not coming) back will produce information about loops in space. These loops, or $1$-cycles, are used to detect tunnels in the Universe.
There might also be voids and, since the Universe is $3$-dimensional, it might also have $3$-dimensional topological features. Studying these features would require us to add to the existing list, currently containing the point, the line, and the plane, a new item: space, or, more accurately: a 3-dimensional space. How such a space creates a 3-cycle may be hard or impossible to visualize. Nonetheless, these cycles are detectable - by applying the methods presented in this book.
Example. What if the Universe is like a room with two doors and, as you exit through one door, you enter it through the other? You'll realize that, in fact, it's the same door! If you look through this doorway, this is what you see:
$\square$
Exercise. What is the dimension of this feature?
Exercise. What if, as you exit one door, you enter the other - but upside down? Sketch what you would see.
Elsewhere, we have to face even higher dimensions...
Patterns in data
Data resides outside of our tangible, physical, $3$-dimensional world.
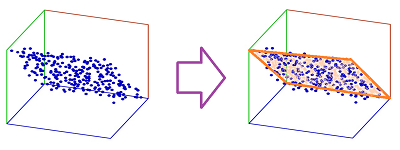
Suppose we conduct an experiment that consists of a set of $100$ different measurements. We would, of course, like to make sense of the results. First, we put the experiment's results in the form of a string of $100$ numbers. Next, thinking mathematically, we see this string as a point in the $100$-dimensional space. Now, if we repeat the experiment $1000$ times, the result is a “point cloud” of $1000$ points in this space:
Now, as scientists, we are after patterns in data. So, is there a pattern in this point cloud and maybe a law of nature that has produced it? What shape is hinted by the data?
But our ability to see is limited to three dimensions!
Exercise. What is the highest dimension of data your spreadsheet software can visualize? Hint: colors.
With this limited ability to visualize, we still need to answer the same questions about the shape outlined by the point cloud:
- Is it one piece or more?
- Is there a tunnel or a void?
- And what about possible 100-dimensional topological features?
Once again, we can't step outside and take a look at this object.
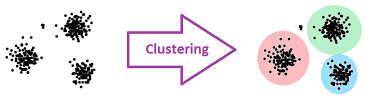
The first question is the most important as it is the question of classification. Throughout our evolution, we've relied on classifications, and we still do: drugs, customers, movies, species, web sites, etc. The methods for solving this problem of classification - often called “clustering” - are well-developed in data analysis:
The rest of the questions will require topological thinking. The methods for solving this problem are presented in this book. We will record cycles of all dimensions in the data and, through purely algebraic procedures, detect its topological features:
They are called homology classes.
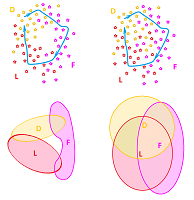
Example (garden as data). Here is an example of data analysis one can do without a computer. Imagine you are walking through a field of flowers: daffodils, lilies, and forget-me-nots. You are blindfolded but you can detect the smells of the flowers as you walk, in this order:
- daffodils only, then
- daffodils and lilies, then
- lilies only, then
- lilies and forget-me-nots, then
- forget-me-nots only, then
- daffodils and forget-me-nots,
- daffodils only again.
Now, thinking topologically, you might arrive at an interesting conclusion: there is a spot in the field, for which it is either true that:
- none of these types of flowers grow there, or
- all three types of flowers grow there.
The reason why is illustrated below:
Of course, the conclusion fails if any of the types grows in several separate, disconnected patches.
$\square$
Exercise. What if the patches are connected but might have holes in them?
Social choice
Next, we present examples of how the presence of topological features in the space of choices may cause some undesirable outcomes.
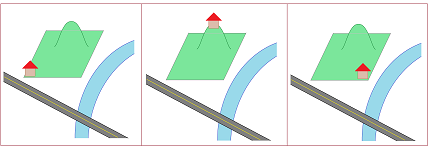
Suppose the owner of a piece of land needs to decide on the location for his new house based on a certain set of preferences. Suppose the land varies in terms of its qualities: grass/undergrowth/forest, hills/valleys, wet/dry, distance to the road/river/lake, etc. If the landowner only had a single criterion for his choice, it would be simple; for example, he would choose the highest location, or the location closest to the river, or closest to the road.
However, what if, because of this variety of possible locations and the complexity of the issues, the owner can only decide on the relative desirability of locations, and only for locations in close proximity to each other? Is it possible to make a decision, a decision that satisfies his preferences?
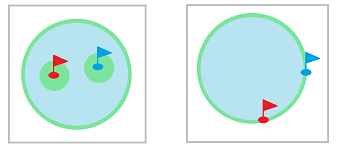
Let us first suppose that the piece of land consists of two separate parcels. It follows that no two sites located in different parcels are considered “nearby”! Therefore, the comparison between them is impossible and the answer to our question is No. This observation suggests that the question may be topological in nature.
What if the land parcel is a single piece but there is that lake in the middle of it? We will prove later in this book that the answer is still No.
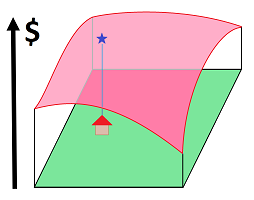
Ideally, the preferences are expressed by a single number assigned to each location: the larger its value, the better the choice. These numbers form what's called a “utility function”:
This function may have a monetary meaning in the sense that building the house will increase the value of the real estate by an amount that depends on the chosen location.
We will prove two facts in this book. First, whenever the piece of land is known to be acyclic, there inevitably is a utility function. Second, a piece of land that always has a utility function has to be acyclic.
So, what prevents us from constructing such a function for a non-acyclic parcel? Let's consider a piece of land that is a thin strip along a triangular lake. Suppose the locations within any of the three sides of the triangle are comparable but there is no comparison between the edges:
The result could be a cyclic preference!
Such preferences are seen elsewhere. A small child may express, if asked in a certain way, a circular preference for a Christmas present: $$bike \quad > \quad videogame \quad > \quad drum\ set \quad > \quad bike \quad > \quad ...$$
In another example, suppose we have three candidates, $A$,$B$, and $C$, running for office and there are three voters with the following preferences: $$\begin{array}{cccc} \hline & \mbox{First choice} & \mbox{Second choice} & \mbox{Third choice} \\ \hline \mbox{Voter } 1: & A & B & C\\ \mbox{Voter } 2: & B & C & A\\ \mbox{Voter } 3: & C & A & B\\ \hline \end{array}$$ Who won? Is it candidate $C$? No, because one can argue that $B$ should win instead as two voters ($1$ and $2$) prefer $B$ to $C$ and only one voter ($3$) prefers $C$ to $B$. Then, the same argument proves that $A$ is preferred to $B$, and then $C$ is preferred to $A$. Our conclusion is: sometimes a seemingly reasonable interpretation of collective preferences can be cyclic, even if the preferences of individual voters are not.
And let's not forget about: $$rock\quad > \quad paper \quad > \quad scissors \quad > \quad rock \quad > \quad ...$$
Exercise. Think of your own examples of cyclic preferences, in food, entertainment, or weather.
This is not to say that these preferences are unreasonable, but only that they cannot be captured by a utility function. In particular, we can't assign dollar values to the locations when the preferences are cyclic. We are also not saying that there is no way to make a choice when there is a lake in the middle of the parcel, but only that we can't guarantee that it will always be possible.
Next, let us assume that it is possible.
Suppose the landowner is able to choose a location based on his preferences, or in some other way. What if, however, the landowner's wife has a different opinion? Can they find a compromise?
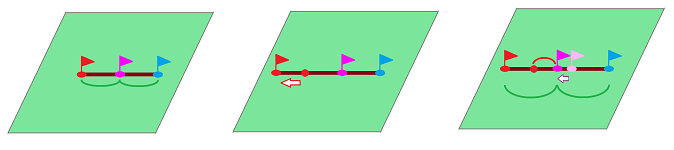
The goal is to have a procedure ready before their choices are revealed. The idea is that as the two of them place -- simultaneously -- two little flags on the map of the land, the decision is made automatically:
- to every pair of locations $A$ and $B$, a third, compromise, location $C$ is assigned ahead of time.
The obvious method is: chose the midpoint. However, just as before, this method fails if the land consists of two separate parcels.
Exercise. Sometimes this midpoint method fails even if the parcel isn't disconnected, such a U-shape. Find an alternative solution.
We already know that the next question to be asked is, is it is always possible to find a fair compromise when there is a lake in the middle? The method may be: choose the midpoint as measured along the shore. However, what if they choose two diametrically opposite points? Then there are two midpoints!
An amended method may be: choose the midpoint and, in case of diametrically opposite choices, go clockwise from $A$ to $B$. This method, however, treats the two participants unequally...
Exercise. Suggest your own alternative solutions.
Again, we can guarantee that such a fair compromise-producing procedure is possible but only if the land parcel is known to be acyclic. This subtle result will be proven in this book. The result implies that there may be a problem when a jointly owned satellite is to be placed on a (stationary) orbit. We will also see how these topological issues create obstacles to designing a reasonable electoral system.
This isn't the end of the story though... Suppose the husband and wife have placed their little flags, $A$ and $B$, on the map of their land and then applied the procedure designed in advance, to place the third flag, $C$, at the compromise location. Imagine now that as the wife leaves the room, the husband moves his flag in the direction away from the wife's. Then he also moves flag $C$ as well to preserve the appearance of a fair compromise. As a result of this manipulation, flag $C$ is now closer to the husband's ideal location!
However, as the husband leaves the room, the wife enters and makes a similar move! And the game is on...
Such a backward movement resembles a tug-of-war.
Now, as the game goes on, one of them reaches the edge of the parcel. Then he (or she) realizes that there is no further advantage to be gained. While the other person continues to improve her (or his) position, eventually she (or he) too discovers that she (or he) is not gaining anything by moving further back. It's a stalemate!
Exercise. Try this game yourself -- on the square and other shapes -- using the midpoint method for finding the compromise location. What if the “compromise” is chosen to be twice as close to your ideal location than to the other?
This stalemate is thought of as an equilibrium of the game. Indeed, neither can improve one's position by a unilateral action.
Again, we can guarantee that such an equilibrium exists but only if the land parcel is known to be acyclic. We will demonstrate how the topology behind this situation applies to other games as well as the equilibrium of a market economy.
Exercise. Try to play this game on the shore of a lake using the amended midpoint method described above. Show that there is no equilibrium.