This site is being phased out.
Homology classes
Contents
Topological features of objects
At the very beginning of our study of topology we are interested in the following visible features of everyday objects:
- cuts/gaps,
- holes/tunnels, and
- voids/bubbles.
Let's try to describe these features mathematically.
In order to make this study independent of a lengthy development of point-set topology, we will initially limit ourselves to the study of
The continuity of functions $$f:X\to Y\subset {\bf R}^M$$ between such sets is explained in calculus: it is understood via its coordinate functions $$f_i:{\bf R}^N \to {\bf R},\ i=1,2,...,M,$$ each of which is continuous with respect to each of its variables.
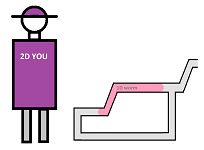
First, we need to recognize that even though we describe these properties as visible features, our interest is the intrinsic properties. The intrinsic properties are the ones that you can detect from within the object.
For example, in the $1$-dimensional case one can think of a worm moving through a system of tubes. The topology the worm can feel and detect is limited to the forks of the tube. It might also discover that it can come back to the beginning point of its journey:
Meanwhile, we, the humans, can see the whole thing by being outside, in the $2$-dimensional space.
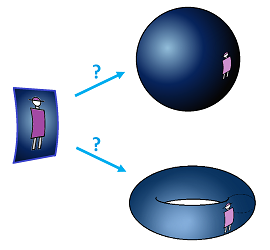
On the other hand, we, the humans, couldn't tell whether the surface of the Earth is a sphere or a torus if it were always covered by fog or darkness:
Finally, intrinsic properties are the only properties that we can hope to capture when we study the topology of our $3$-dimensional universe. An example of such a property is a room you are walking out of and simultaneously entering through another door (maybe upside down!).
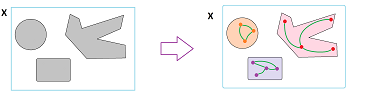
Let's examine, informally, a mathematical meaning of topological features of subsets of the Euclidean space. We will first consider featureless objects.
Recall that we capture topological features of space $X$ by means of cycles of dimensions $0$, $1$, and $2$. Of course, we can draw them anywhere in $X$; such as these:
- 0. two points,
- 1. circle, and other closed curves,
- 2. sphere, and other closed surfaces.
For $X$ to be a featureless object, all of its cycles have to be trivial in a sense. The triviality is understood as our ability to “fill” the opening of the cycle, or its ability to contain or “bound” something in $X$, as follows.
Cuts/gaps:
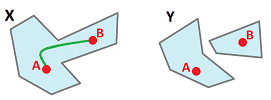
- the gap between every two points in $X$ can be “filled” with a curve in $X$.
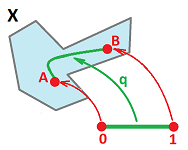
There is a simple and precise way to describe this: $X\subset {\bf R}^N$ is called path-connected, if for any two points $A, B$ in $X$ there is a continuous function $q: [0,1] \to X$ such that $q(0)=A$, $q(1)=B$, i.e., it is a path connecting these two points:
Exercise. Prove that any convex set is path-connected.
Exercise. Prove that the circle is path-connected.
Holes/tunnels:
- the hole in every closed curve in $X$ can be “filled” with a surface in $X$.
Exercise. Does the sphere have a non-trivial $1$-cycle? Illustrate your answer with a picture. What about the torus?
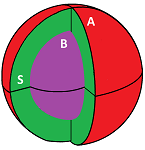
Voids/bubbles:
- the void in every closed surface in $X$ can be “filled” with a solid in $X$.
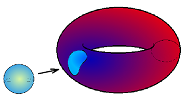
Even tough we are after the bubbles here, we don't limit ourselves to just spheres. The reason is that otherwise we would miss the void of the torus. As you can see any sphere on the torus has to be flattened:
Exercise. Give an example of a trivial $3$-cycle.
“Filling” gaps is usually understood as the ability to connect the two points to each other -- by a curve. “Filling” holes and voids can also be understood this way: $$\begin{array}{c|c|lll|c} \text{featureless} & \text{dim} & \text{a feature} & \text{is trivialized} &\text{by a filling} & \text{dim} \\ \hline \text{no gaps} & 0& \text{any two points} & \text{are connected by} & \text{a curve} & 1\\ \text{no tunnels} & 1 & \text{any closed curve} & \text{is connected to itself by} & \text{a surface} & 2\\ \text{no voids} &2 & \text{any closed surface} & \text{is connected to itself by} & \text{a solid} & 3 \end{array}$$ The relation between the dimensions becomes clear: a $k$-dimensional gap is filled with a $(k+1)$-dimensional object.
How to define and count $0$-dimensional features
Let's review. We want our mathematical interpretations of the topological features to satisfy the following criteria:
$\bullet$ 1. The description should include no measuring. This way the features are preserved under stretching, bending etc.
$\bullet$ 2. The description can be verified by looking from the inside of the object. This way the features are independent from how $X$ might fit into some $Y$.
$\bullet$ 3. The description should be quantitative. Then, without measuring, what's left is counting.
Let's test the above definitions against these criteria. The first two are easily satisfied. But how quantitative is it? So far, we are only able to say Yes or No: connected or not, trivial or non-trivial, etc. Without counting of the features there is no evaluation of the topology of $X$!
We will have to go deeper.
We start with dimension $0$ with the goal of learning how to count the topological features -- based somehow on the definition of path-connectedness. However, we would like to count not the number of cuts but the number of pieces of the object instead. The reason is that the former concept is ambiguous: one can cut a cake into $4$ pieces with $4$ cuts or with $2$ cuts!
As there may be infinitely many points in each piece, it wouldn't make sense to count those. We need a way to resolve this ambiguity. We observe that in the definition the two points are connected to each other by a curve. Hence the idea:
- instead of counting the pieces directly, we count points, but,
- we count two of them only once if they are connected to each other by a path.
This way we don't count points, we count classes of points.
This analysis suggests that we are dealing with an equivalence relation. This equivalence relation is called homology and the equivalence classes are called homology classes.
Definition. We say that two points $A$ and $B$ in $X$ are homologous if there is a continuous function
These paths are nothing but parametric curves. Of course, self-intersections are allowed:
Theorem. Homology is an equivalence relation.
Proof. We recall and prove the three axioms.
Reflexivity: $A \sim A$. A point is connected to itself; just pick the constant path, $q(t) = A, \forall t$.
Symmetry: $A \sim B \Rightarrow B \sim A$. If path $q$ connects $A$ to $B$ then $p$ connects $B$ to $A$; just pick $p(t) = q(1-t), \forall t$.
Transitivity: $A \sim B$, $B \sim C \Rightarrow A \sim C$. If path $q$ connects $A$ to $B$ and path $p$ connects $B$ to $C$ then there is a path $r$ that connects $A$ to $C$; just pick: $$r(t) = \begin{cases} q(2t) & \text{for }t \in [0,1/2], \\ p(2t-1) & \text{for }t \in [1/2,1]. \end{cases}$$ $\blacksquare$
Exercise. Sketch illustrations for the three axioms above.
Exercise. Provide the missing details in the above proof. Hint: use the definition of continuity from calculus.
Exercise. (a) Provide an alternative definition based on a path given by $q : [a,b] \to X$. (b) Prove that this new definition gives an equivalence relation. (c) Prove that the two definitions are equivalent.
A couple of facts about equivalence relations:
- The equivalence classes are disjoint.
- Their union is the whole set.
In other words, we have a partition of $X$. The homology class of point $A$ in $X$ is denoted by $[A]$. Every point in $[A]$ can be reached from $A$, therefore any pair of points can be connected by a curve that lies entirely in $X$.
We have partitioned $X$ into $0$-dimensional homology classes, called path-components.
Exercise. Suppose $f:X\to Y$ is continuous. Prove that $$A\sim B \Rightarrow f(A) \sim f(B).$$ Hint: the composition of two continuous functions is continuous.
How to define and count $1$-dimensional features
Next, how do we capture holes and tunnels?
Giving these simple words an unambiguous meaning may be a challenge, as this picture demonstrates:
Where is the beginning and where is the end of a tunnel? If two tunnels merge, is this one tunnel or two? What if the tunnel splits? And then merges with another one? And so on.
To start with the simplest case, what captures the hole of a doughnut?
Our ability to put a finger through the hole isn't what we want. Remember, we want to describe features of objects in such a way that you can detect them from the inside the object.
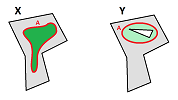
Curves in $X$ would qualify. Indeed, the loops, i.e., $1$-cycles, that go around the hole do capture that hole:
Meanwhile, loops that don't go around the hole capture nothing; they are “trivial”.
This is a good start but, just as with the points, there are infinitely many of these loops and it would be pointless to try to count them. Fortunately, from the discussion of dimension $0$, we know that a good way to resolve this might be to establish an equivalence relation between loops in $X$.
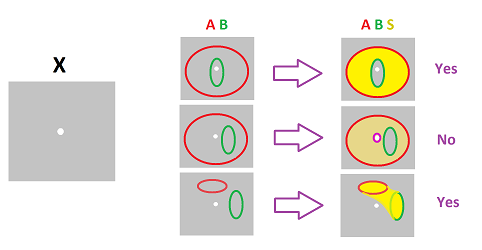
Recall that if $1$-cycle $L$ does not catch any tunnels, i.e., it's trivial, when it bounds a surface $S$ in $X$.
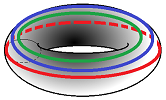
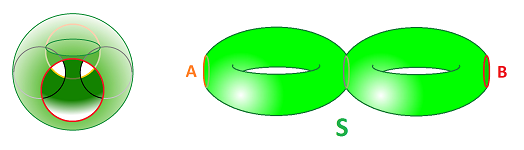
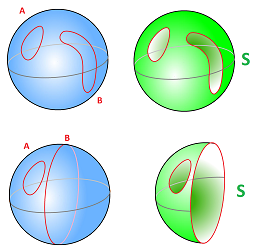
Now, what if $1$-cycle $L$ consists of two loops, $A$ and $B$? And what if these two loops -- together -- bound a surface $S$?
If such an $S$ exists, we think of $A$ and $B$ as equivalent! This way we avoid double counting:
There is now exactly one, it appears, equivalence class of loops that goes around the hole. Or is there? What about the loops that go around it twice or thrice?
Are they all homologous to each other? How to define homology in this more general setting is discussed in the next subsection. However, the answer is No, they are not all homologous to each other. Only the loops with the same number of turns around the hole (in the same direction!) are homologous. But then we have infinitely many homology classes for a single hole! We resolve this issue by taking an algebraic point of view; by counting the number of turns we have established a correspondence between the set of all these classes and the set of integers ${\bf Z}$. But the integers are all multiples of a single number, $1 \in {\bf Z}$. In that sense, the homology class that corresponds to $1$ "generates" the rest of them. That's why it is the only one that counts.
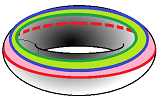
The simplest example of a surface connecting two loops is a cylinder or a ring. One can then justify calling these loops $A$ and $B$ equivalent by observing that we can gradually transform one into the other using the surface that connects them:
These loops are also called homotopic and spaces with all loops homotopic to each other are called simply-connected.
However, in the general $3$-dimensional case, $S$ might look like this:
Exercise. Give formulas of continuous functions: (a) of the line that creates a loop, (b) of the plane that creates a loop, (c) of the plane that creates a void.
Homology as an equivalence relation
Let's review how we have introduced homology as an equivalence relation. Points $A$ and $B$ are homologous if there is a path between them. What if $A$ and $B$ are curves?
Then we need to fill in the blank space below:
The analogy is visible:
Let's compare:
- dimension $0$: points $A \sim B$ if there is a curve between them.
- dimension $1$: curves $A \sim B$ if there is a ????? between them.
We see that the dimensions go up by one:
- from $0$ to $1$: “points” is replaced with “curves”, and
- from $1$ to $2$: “curve” is replaced with its $2$-dimensional counterpart: “surface“!
So, this is what we have: loops $A \sim B$ if there is a surface $S$ “between them”. The key insight here is the relation between $S$ and $A \cup B$: the latter is the boundary of the former.
The definition then becomes:
- Two closed curves (loops) $A$ and $B$ are homologous if there is a surface $S$ such that $A$ and $B$ form its boundary.
Exercise. Sketch illustrations for the axioms of equivalence relations for the $2$-dimensional homology.
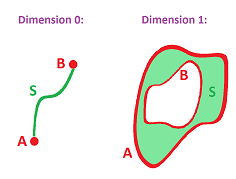
Our observation about the meaning of “between them” allows us to go back to the $0$-dimensional case and discover that the end-points $A,B$ of the curve should also be understood as its boundary!
To make the first step toward higher dimensions, let's consider this list:
- dimension $0$: points $A \sim B$ if there is a curve $S$ between them.
- dimension $1$: curves $A \sim B$ if there is a surface $S$ between them.
- dimension $2$: surfaces $A \sim B$ if there is a solid $S$ between them.
The relation described in the last item is illustrated below by the inner and outer surfaces of this spherical shell (a “thick sphere”):
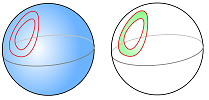
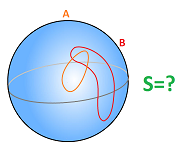
Example. Let's consider these two loops $A,B$ on a sphere:
This is what we observe:
- They are homologous.
- The surface $S$ is the whole sphere minus the inside of $A, B$.
We conclude that there are no tunnels on this sphere.
$\square$
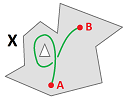
Exercise. Or volcanoes: is this loop homologous to a point?
Exercise. Discuss the homology of surfaces by sketching two pairs of examples for each of the surfaces below: (a) two closed curves, preferably not too close to each other, that are homologous; (b) two closed curves that are not homologous, if possible.
In general, the explanation that “$S$ is the whole sphere minus the inside of $A, B$” in the above example is incorrect as this illustration shows:
The reason is that there is no meaning for “inside” of a curve on a sphere!
The next illustration suggests that whatever $S$ is, it's not really a surface:
The problem is easier to recognize in these three examples of pairs of homologous and non-homologous loops in the punctured plane:
In the last example, the surface that connects the two loops, which is simply a cylinder, is flattened by being “crushed” into the plane.
The way to straighten this out is to realize that just as we allow the curves in the $0$-dimensional case to self-intersect, we allow the same for these surfaces; we are dealing with parametric curves and parametric surfaces.
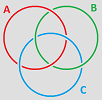
Exercise. What is the homology class of $A$ in ${\bf R}^3 \setminus (B \cup C)$?
This approach taken to its logical end leads to a special kind of homology called “bordism”. Instead, in the rest of the book we replace the phrase “curve, surface, and solid” with “something made of elementary $1$-dimensional, $2$-dimensional, and $3$-dimensional pieces”. Then, the crucial part of our study will be about
- how the $n$-dimensional pieces are attached to each other along their $(n-1)$-dimensional boundaries.
We will start in the next section with graphs ($n=1$).
Homology in calculus
We will consider three well-known theorems from elementary calculus.
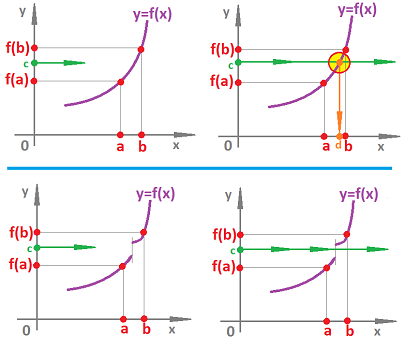
Theorem (Intermediate Value Theorem). Suppose $f : [a,b] \to{\bf R}$ is continuous. Then for any $c$ between $f(a)$ and $f(b)$, there is $d \in [a,b]$ such that $f(d) = c$.
Exercise. Is continuity a necessary condition?
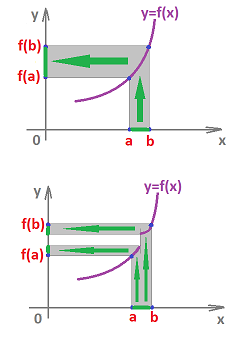
What does this have to do with homology? The theorem tells us that the image of a path-connected interval is also a path-connected interval, under a continuous function:
We can even use this theorem to evaluate the topology. We conclude: a continuous function doesn't increase the number of path-components. The theorem will be proved in a higher generality later in the text.
Next, let's test how well you know calculus.
Calculus 1 question: “What is the antiderivative of $1/x$?”
Calculus 1 answer: “It's simply $F(x)=\ln|x|+C$!”
Wrong!
Why wrong? Hint: $1/x$ undefined at $0$.
Exercise. The question is wrong, too! Explain how.
First, what is our formula intended to mean? The $+C$ in the formula indicates that
- we have captured infinitely many -- one for each real number $C$ -- antiderivatives, and
- we have captured all of them.
And we would have -- if it were any other, continuous, function $f$ -- the following result:
where $F_0$ is any given antiderivative of $f$.
But the domain of $1/x$ consists of two rays $(-\infty, 0)$ and $(0, +\infty)$. That's two separate path-components!
As a result, we can, correctly, solve this problem separately on each, as follows. All antiderivatives are represented by:
- $f_-(x)=\ln(-x)+C$ on $(-\infty, 0)$, and
- $f_+(x)=\ln(x)+C$ on $(0, +\infty)$.
But now we want to combine each of these pairs of functions into one, $f$, defined on $(-\infty, 0)\cup (0, +\infty)$. Then we realize that, every time, the two constants might be different: after all, they have nothing to do with each other!
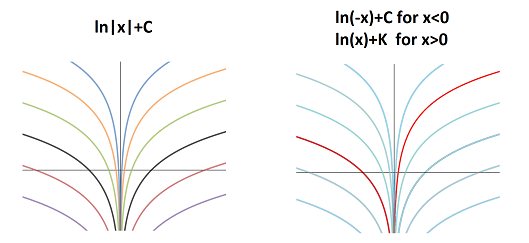
We visualize the wrong answer on the left and the right on the right:
The formula and the image on the left suggest that the antiderivatives are even functions. The image on the right shows only one antiderivative but its two branches don't have to match!
Algebraically, the correct answer is given by $$ F(x)=F_{C,K}(x) := \begin{cases} \ln(-x)+C & \text{ for } x \in (-\infty, 0), \\ \ln(x)+K & \text{ for } x \in (0, +\infty) \end{cases} $$
Exercise. Verify that this is an antiderivative of $1/x$.
This family of functions isn't parametrized by the reals ${\bf R}$ anymore, but, with two parameters, by ${\bf R}^2$. The exponent reflects the number of components of the domain. Moreover, it is insightful to think of the set of antiderivatives splitting into equivalence classes, one for each component.
Exercise. Define these classes.
Question: But isn't $F$ supposed to be continuous? Because it doesn't look continuous...
Exercise. Verify that it is. Hint: check point-wise.
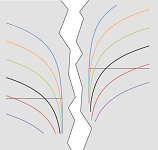
This is how we see the disconnected reality resulting in two disconnected calculi:
Next, one might recall something else from Calculus:
“Theorem”. If $F'=0$ then $F$ is constant.
But this isn't the whole story, as we just saw.
Let's restate properly.
Theorem. Given a function $F:X \to {\bf R}$, where $X$ is an open subset of ${\bf R}$, and
- $F$ is differentiable on $X$,
- $F'(x)=0$ for all $x \in X$.
Then $F$ is constant, provided $X$ is path-connected.
Exercise. Give an example of a disconnected $X$ for which the conclusion of the theorem fails.
Exercise. Restate the theorem for a disconnected $X$.
Less precise, for now, are the ideas related to the role of holes in calculus. Recall that a vector field is a function $f : {\bf R}^2 \to {\bf R}^2$. It is called conservative on a region $D$ if it is the gradient of a scalar function: $F = \operatorname{grad} f$.
Theorem. Suppose $F=(P,Q)$ and $P_y=Q_x$ on region $D$. Then $F$ is conservative provided $D$ is simply-connected.
Exercise. In light of this analysis, discuss Escher's Waterfall.
We have demonstrated the importance of the interaction between Calculus and Topology. Above are examples of something very common:
- $\longrightarrow$ Given $X$, if we know its topology, we know a lot about calculus on $X$.
- $\longleftarrow$ Given $X$, if we know calculus on it, we know a lot about the topology of $X$.