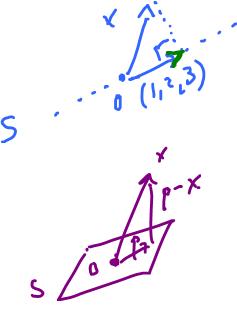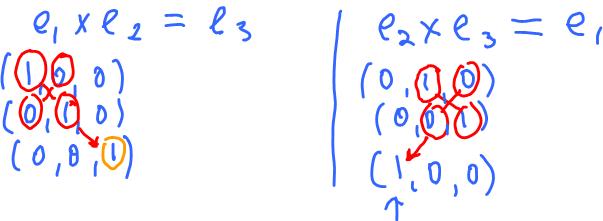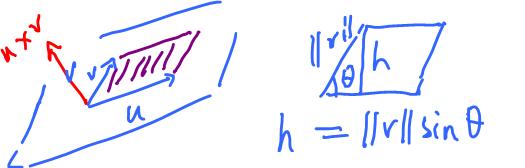Geometry of Euclidean space

The length of vectors, the norm

In order to develop the geometry of vectors we need to be able to see when they are the same, when they are different, and by how much. To compare, we can measure lengths of vectors and the angle between them.

More precisely, this is simply the difference between the vectors, i.e., another vector, and its length is the measure of the difference between them.

$$||PQ|| = {\rm \hspace{3pt} Length \hspace{3pt} of \hspace{3pt}} OP - OQ$$

The length of a vector is called the "norm". Compare to the $1$-dimensional case:

In ${\bf R}$: vector $v$ is a number, so $||v|| = |v|$ is the absolute value
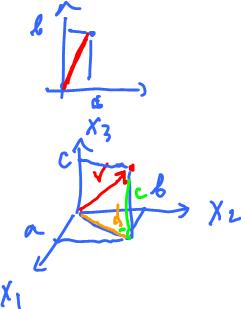
In ${\bf R}^2$: $v$ is a pair of numbers $(a, b)$ then $||v|| = (a^2 + b^2)^{\frac{1}{2}}$. This is a Pythagorean theorem (Image)
In ${\bf R}^3$: what is the norm of $v$, which is a triple of numbers, $||v|| =?$

Using the Pythagorean Theorem three times: $$\begin{array}{} d^2 &= a^2 + b^2, \\ ||v||^2 &= c^2 + d^2, {\rm \hspace{3pt}} so \\ ||v||^2 &= c^2 + a^2 + b^2. \end{array}$$

In ${\bf R}^n$: when $v = (x_1, ..., x_n)$, what is the norm of $v$?

Definition. The norm of $v \in {\bf R}^n$ is $$||v|| = (x_1^2+x_2^2+ \ldots + x_n^2)^{\frac{1}{2}},$$

Properties.

$||v|| \geq 0 , |||v||| = 0$, if $v = 0$: Positivity;
$||\alpha v|| = |\alpha | \cdot ||v||$ for any $\alpha \in {\bf R}$: Homogeneity;
$||u + v|| \leq ||u|| + ||v||$: Triangle Inequality.

The properties are more important than the definition or the formula as it's often the case.

Example. $||(1,1,1,1, \ldots ,1)||$ , here $1$ repeated $n$ times , so
$= (1^2 +..+ 1^2)^{\frac{1}{2}}$ repeated $n$ times
$= \sqrt{n}$.

Example. $$\begin{array}{} ||(1,1,1)|| = \sqrt{3}; \\ ||(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}})|| = ||\frac{1}{\sqrt{3}}(1,1,1)||^2 = \frac{1}{\sqrt{3}}||(1,1,1)|| = \frac{1}{\sqrt{3}} \times \sqrt{3} = 1, {\rm \hspace{3pt} a \hspace{3pt} unit \hspace{3pt} vector;} \\ \end{array}$$

$(1,0, \ldots, 0)$ unit vector in ${\bf R}^n$;
$(0,1,0, \ldots, 0)$ unit vector in ${\bf R}^n$;
$(\frac{1}{\sqrt{n}},\frac{1}{\sqrt{n}}, \ldots ,\frac{1}{\sqrt{n}})$ unit vector in ${\bf R}^n$.

Given a vector $v \neq 0$, then $u = \frac{v}{||v||}$ is a unit vector.

Based on the formula for the norm, we have the distance formula for ${\bf R}^n$ (Image) $$d(x, y) = ||x - y||.$$

The properties are more important than the formula:

$||x|| \geq 0, ||X|| = 0$ iff $x = 0$;
$||\alpha x|| = ||\alpha || \cdot ||X||$;
$||x + y|| \leq ||x|| + ||y||$.

(The whole is larger than the sum of the parts, NOT!)

Angles between vectors

As we shall see the inner product of two vectors defined by

$$<X,Y> = X_1Y_1 + \ldots + X_nY_n$$

reveals the angle between them. Compare to the norm:

$$||x||^2 = x_1^2 + ... + x_n^2.$$

Then $$<x,x> = ||x||^2.$$

Example. Let's experiment with these unit vectors:

$<(1,0),(0,1)> = 1 \cdot 0 + 0 \cdot 1 = 0$ (This suggests: vectors are perpendicular $\rightarrow <X,Y> = 0$.);
$<(0,1),(-1,0)> = 0 \cdot (-1) + 1 \cdot 0 = 0$;
$<(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}),(\frac{-1}{\sqrt{2}}, \frac{1}{\sqrt{2}})> = -\frac{1}{2}+\frac{1}{2} = 0.$
$x$ unit vector:
$<x,x> = ||x||^2 = 1^2 = 1$;
If $\alpha = \frac{\pi}{2}$ then $<x,y> = 0 \rightarrow {\rm cos \hspace{3pt}} \frac{\pi}{2} = 0$;
If $\alpha = 0$ then $<x,y> = 1 \rightarrow {\rm cos \hspace{3pt}} 0 = 1$.

$$\begin{array}{} <x_1-x> &= x_1|-x_1| + x_2| - x_2| \\ &= -x_1^2 - x_2^2 \\ &= -(x_1^2 + x_2^2) \\ &= -||x||^2 \\ &= -1 \rightarrow {\rm cos \hspace{3pt}} \pi = -1 \end{array}$$

What about non-unit vectors?

Theorem (Properties of the inner product).

$<x,x> \geq 0, <x,x> = 0$ iff $x = 0$: Positivity
$<x,y> = <y,x>$ for all $x$: Symmetry
$<\alpha x,y> = \alpha <x,y>$: Homogeneity
$<x,y + z> = <x,y> + <x,z>$: Distributivity

Proof. 3: $$\begin{array}{} <\alpha x, y> &= (\alpha x_1)y_1 + (\alpha X_2)Y_2+ \ldots +(\alpha X_n)Y_n \\ &= \alpha (x_1y_1 + \ldots + x_ny_n) \\ &= \alpha <x,y> \end{array}$$

4: Simple

(Again, properties are more important than the formula.)

Theorem. If $u, v$ are unit vectors, then

$$ = {\rm cos \hspace{3pt}} \alpha ,$$

where $\alpha$ is the angle between them.

What if $X,Y$ are not unit vectors? The angle between $X,Y$ is the same as that between the corresponding unit vectors, i.e., $$\frac{X}{||X||}, \frac{Y}{||Y||},$$ as follows:

$${\rm cos \hspace{3pt}} \alpha = <\frac{X}{||X||}, \frac{Y}{||Y||}> = \frac{1}{||X||} \cdot ||Y|| <X,Y>.$$

From the above statement,

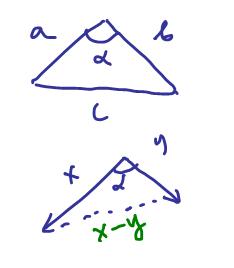
Theorem. For any two vectors, $$<X,Y> = ||X|| \cdot ||Y||{\rm cos \hspace{3pt}}\alpha ,$$

where $\alpha$ is the angle between them.

Proof. Recall the Law of Cosines: $$c^2 = a^2 + b^2 - 2ab{\rm cos \hspace{3pt}}\alpha$$

Re-write for $$a = ||X|| {\rm \hspace{3pt} and \hspace{3pt}} b = ||X||.$$

Then $$c^2 = ||X||^2 + ||Y||^2 - 2||X|| \cdot ||Y||{\rm cos \hspace{3pt}}\alpha .$$ Also

$$\begin{array}{} c^2 &= ||X - Y||^2 \\ &= <X - Y,X - Y> \\ &= <X,-Y> + <X,X> + <-Y,X> + <-Y,-Y> \\ &= -<X,Y> + ||X||^2 - <X,Y> + ||Y||^2. \end{array}$$

So $$c^2 = ||X||^2 + ||Y||^2 - 2||X|| \cdot ||Y||{\rm cos \hspace{3pt}}\alpha = -<X,Y> + ||X||^2 - <X,Y> + ||Y||^2.$$

Canceling similar terms on both sides, $$-2||X|| \cdot ||Y||{\rm cos \hspace{3pt}}\alpha = -2<X,Y>, {\rm \hspace{3pt}} or$$

$$<X,Y> = ||X|| \cdot ||Y||{\rm cos \hspace{3pt}}\alpha .$$

QED

Exercise. Prove $$||X|| = <X,X>^{\frac{1}{2}} {\rm \hspace{3pt} is \hspace{3pt} always \hspace{3pt} a \hspace{3pt} norm.}$$

Cauchy Schwarz Inequality $$|<X,Y>| = ||X|| \cdot ||Y||.$$

Proof. Follows from the previous theorem: $$ <X,Y> = ||X|| \cdot ||Y||{\rm cos \hspace{3pt}}\alpha .$$

Then $$\begin{array}{} |<X,Y>| &= | ||X|| \cdot ||Y||{\rm cos \hspace{3pt}}\alpha | \\ &= ||X|| \cdot ||Y|||{\rm cos \hspace{3pt}}\alpha | , {\rm \hspace{3pt} since \hspace{3pt}} |{\rm cos \hspace{3pt}}\alpha | < 1 \\ &< ||X|| \cdot ||Y||. \\ {\rm QED} \end{array}$$

Let's notice now that even though they are defined via coordinates, the norm and the inner product are independent of the choice of the basis of ${\bf R}^n$:

Projections of vectors

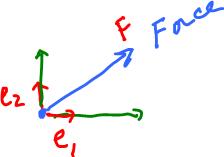
Let's consider the issue of decomposition of forces. The issue is important in physics as one may encounter the case when a force is applied partially against an obstacle such as a wall. In this case, the part of the force that pushes into the wall is "wasted".

For example, the problem may be posed as follows: Represent the given vector $F$ as a linear combination of two vectors $e_1$ and $e_2$: $$F = \alpha e_1 + \beta e_2.$$

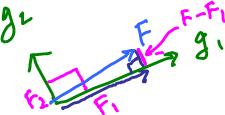
These don't have to be basis vectors, but we will assume that they are perpendicular to each other, for simplicity. When $g_1$ is orthogonal to $g_2$, find vectors $F_1$ and $F_2$ such that

$F = \alpha g_1 + \beta g_2$ (as above) and $\alpha g_1 = F_1$ and $\beta g_2 = F_2$.

Vector $F_1$ is the "projection" of $F$ onto $g_1$. We also say that we "project" $F$ onto $g_1$.

Angle $= \frac{\pi}{2}$ between $g_1$ and $F - F_1$, hence $$<g_1, F - F_1> = 0.$$

Use this information to find $F_1$.

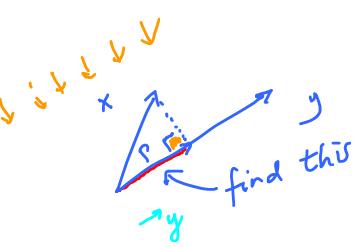
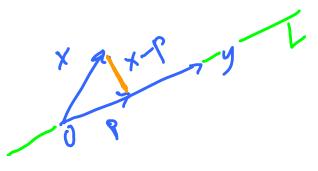
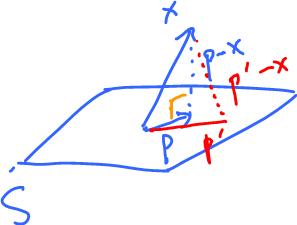
Problem and definition. Given vector $x$ and vector $y$, find the (?) projection $P$ of $x$ onto $y$, which is a multiple of $y$ such that $p - x \perp y$.

Clearly, the projection does not depend on the norm of $y$, only its direction.

Examples. 1) What if $x$ is a multiple of $y$? Then the projection $P$ of $x$ onto $y$ is $x$.

2) What if $x \perp y$? Then $P = 0$.

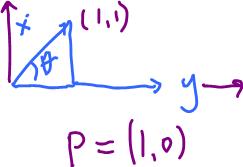
3) Projection of $(1,1)$ on the $x$-axis. $$\theta = \frac{\pi}{4}, {\rm cos \hspace{3pt}} \theta = \frac{2^{\frac{1}{2}}}{2}$$

$$P =(1, 0), P = \alpha y, \alpha = 2^{\frac{1}{2}} \frac{||x||}{2}||y||$$

Now let's solve the problem in full generality:

Given $x,y \neq 0, P = \alpha y, P - x \perp y$, find $\alpha$.

Use the inner product: $$ = 0.$$

Substitute $$<\alpha y - x, y> = 0,$$

solve for $\alpha$. Use properties, first distributive: $$<\alpha y, y> - <x,y> = 0.$$

Second homogeneity: $$\alpha <y,y> - <x,y> = 0.$$

So, $$\alpha = \frac{<x,y>}{<y,y>}.$$

If $\theta$ is the angle between $x$ and $y$, one can continue, $$\alpha = ||x|| \cdot ||y|| \cdot \frac{{\rm cos \hspace{3pt}} \theta}{||y||^2} = \frac{||x||}{||y||} {\rm cos \hspace{3pt}} \theta .$$

Example: Find the projection $P$ of $(-1,2)$ onto $(3,5)$: $$P = \alpha (3,5).$$

Find $\alpha$: $$\begin{array}{} \alpha &= \frac{<(-1,2), (3,5)>}{||(3,5)||} \\ &= (-3+10)/(9+25) \\ &= -7/34. \end{array}$$

Answer: $P = -\frac{7}{34}(3,5)$.

Projections on subspaces

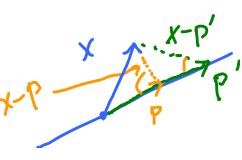
Since only the direction of $y$ matters, we can think of the projection of $x$ onto $y$ as the projection of $x$ onto the ($1$-dimensional) subspace $L$ spanned by $y$:

Projection on $L = $Span$\{y \}$.

But $L$ does not have to be $1$-dimensional...

Conclusions about $P$ and $x - P$:

$P \in L$ but it's special:
$x - P \perp z$ for any $z \in L$.

Next, is it possible that

$x - P^' \perp z$, for some $P^' \in L$?

No, there is only one $P$ such that $x - P \perp L$. Conclusions:

the projection is unique.
the projection gives you the shortest distance to $L$.

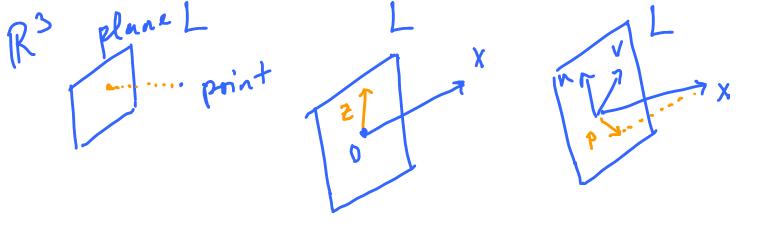
How do we find the shortest distance from a point to a plane? Answer: Find a vector through the point perpendicular to the plane.

Suppose the plane is a linear subspace $L$ and suppose the point is the end of vector $x$. We want:

$x \perp z$ for every $z \in L$,

in other words: $$x \perp L.$$

Since

$L = {\rm span}\{u, v \}$ for some vectors $u,v$, we need only to verify that

$$x \perp u, x \perp v.$$

Why? Because this implies that $x \perp z$ for any $z \in L$. Indeed, Let $z = \alpha u + \beta v$. Then $$\begin{array}{} <z, x> &= <\alpha u + \beta v, x> \\ &= <\alpha u, x> + <\beta v, x> \\ &= \alpha <u, x〉 + \beta <v, x> \\ &= \alpha \cdot 0 + \beta \cdot 0 \\ &= 0. \end{array}$$

Definition. More generally, suppose $S$ is a linear subspace, $X$ is a vector. The projection of $X$ onto $S$ is a vector $P$ satisfying:

$P \in S$;
$P - X \perp S$. (1)

Properties.

$P$ is unique.
$P - X$ is the shortest among all $P' - X$ with $P' \in S$.

Proof. Part 1. Suppose there is $P' \in S$ such that $$P' - X \perp S (2).$$

Show that $P' = P$.

Use $$X = P + (X - P) = P' + (X - P') (1)$$

Use the inner product by $P'$: $$ = < P' + (X - P'), P' >$$

$$< P, P' > + < X - P, P' > = < P', P' > + < X - P',P' >$$

Here $X - P = 0$ by (2) because $P' \in S$ and $X - P' = 0$ by (1) because $P \in S$. Next $$< P, P' > = < P', P' >,$$ $$< P, P' > - < P', P' > = 0 (P = P') $$

Factor it: $$ = 0 => P - P' \perp P'.$$

Try to show that $P - P' \perp P$. Take (1) and multiply by $P$:

$ = < P' + (X - P'), P >$, then
$ + < X - P, P > = < P',P > + < X - P', P >.$

Here $X - P = 0$ by (2) because $P \in S$ and $X - P' = 0$ by (1) because $P' \in S$. Next

$$< P, P > = < P', P >, {\rm \hspace{3pt} some \hspace{3pt} algebra...}$$

(3) $ = 0 \rightarrow P - P' \perp P$ (now proved)

(4) $ = 0 \rightarrow P - P' \perp P'$ (proved previously)

Subtract: (3) - (2). Then

$$ - = 0, {\rm \hspace{3pt} factor}$$

$$ = 0, {\rm \hspace{3pt} or}$$

$$||P - P'||^2 = 0, {\rm \hspace{3pt} so}$$

$$||P - P'|| = 0$$

So, $P - P' = 0$, by positivity, hence $P = P'$. QED

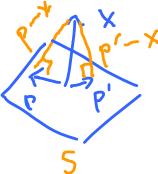
Part 2. This is what we know:

$$P - X \perp S$$

$$P - X \perp P$$

This is a right triangle. Then by Pythagorean Theorem: $$||X||^2 = ||P||^2 + ||P-X||^2$$

Then $$||P - X|| = (||X||^2 - ||P||^2)^{\frac{1}{2}} {\rm (Min \hspace{3pt} over \hspace{3pt} all \hspace{3pt}} P \in S).$$

So,

$$||P - X|| \leq ||P' - X|| {\rm \hspace{3pt} for \hspace{3pt} any \hspace{3pt}} P' \in S.$$

Hence $P' - X$ is not perpendicular to $P'$ ($P' \neq P$). If it was, $P'$ would be the projection. So $P = P'$. QED

Since the projection is unique $P$ is unique, then the following makes sense.

Definition. Define the distance between point $X$ and a subspace $S$ as $||P - X||$.

Example. Let $$S = {\rm span}\{(1,2,3) \}, X =(-1,0,2)$$

Find the projection of $X$ onto $S$. Then $$\alpha (1,2,3) - X ⊥(1,2,3), {\rm \hspace{3pt} so}$$

$$\begin{array}{} \alpha &= \frac{<(1,2,3),(-1,0,2)>}{||(-1,0,2)||^2} \\ &= \frac{-1 + 0 + 6}{1^2+0^2 + 2^2} \\ &= \frac{5}{5} \\ &= 1. \end{array}$$

Answer: $(1,2,3)$.

Example. Find the projection of $X = (1,2,3)$ onto the plane $S$ which is the solution set of $$x_1 + x_2 = 0.$$

First find spanning vectors for $S, u, v$: $$S= Span{u, v}$$

$$u = (1, -1, 0)$$

$$v = (-1, 1, 1)$$

They are linearly independent. Next find $P$, the projection,

$P \in S$, and
$u, v \perp P - X$.

Verify

$P = \alpha U + \beta V$ for some $\alpha , \beta \in {\bf R}$. Find $\alpha , \beta$.
How?
$ = 0,$

$<v, P - X> = 0.$

Substitute

$ = 0,$ and
$<v, \alpha u + \beta v - X> = 0.$

Hence,

$ + + = 0$, and
$< v , \alpha v> + < v , \beta v> + < v , -x> = 0.$

Then

$<\alpha ||u||^2 + \beta - = 0$ and
$< \alpha + \beta ||v||^2 - <v, x> = 0.$

Then $$||u||^2 = 2, ||v||^2 = 3, = -2,$$

$$ = -1, <v, x> = 4.$$

Substitute all these values: $$2\alpha -2\beta + 1 = 0$$

$$-2\alpha +3\beta - 4 = 0$$

Solve it. Add the equations: $$\begin{array}{} -2\beta + 1 + 3\beta -4 = 0 \\ \beta - 3 = 0 \\ \beta = 3, {\rm \hspace{3pt} substitute \hspace{3pt} this \hspace{3pt} value:} \\ 2\alpha - 2(3) + 1 = 0 \\ 2\alpha - 5 = 0 \\ \alpha = 5/2, {\rm \hspace{3pt} so} \\ P = \alpha u + \beta v = 5/2u + 3v. \end{array}$$

Get $P$'s coordinates:

$u = (1, -1, 0)$ and $v = (-1, 1, 1)$, substitute those values:

$$\begin{array}{} P &= \frac{5}{2(1, -1, 0)} + 3(-1, 1, 1) &= (\frac{5}{2}, -\frac{5}{2}, 0) + (-3, 3, 3) &= (-\frac{1}{2}, \frac{1}{2}, 3) \end{array}$$

Further, what is the distance from $X$ to $S$? $$\begin{array}{} = ||X-P|| \\ = ||(1, 2, 3) - (-\frac{1}{2}, \frac{1}{2}, 3)|| \\ = ||(1 \frac{1}{2}, 1 \frac{1}{2}, 0)|| \\ = ((\frac{3}{2})^2 \cdot 2)^{\frac{1}{2}} \\ = \frac{3}{2} \cdot 2^{\frac{1}{2}}. \\ \end{array}$$

Orthogonal vectors

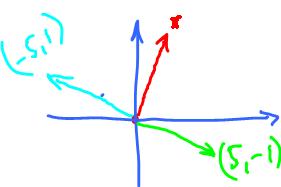
Example. Find $$y = (y_1,y_2) \perp X = (1, 5).$$

Try: $$\begin{array}{} <(5, -1), (1, 5)> &= 5-5 \\ &= 0, \end{array}$$

works!

Unique? $$<(-5, 1), (1, 5)> = 0. {\rm \hspace{3pt} No}.$$

You can also try the corresponding unit vectors: $$u = \frac{(5, -1)}{||5,-1||} = \frac{(5, -1)}{26^{\frac{1}{2}}}$$

What about all vectors perpendicular to $x$? Let's call this set $S$. What is $S$? A line: $$S = {\rm span}\{(-5,1) \}$$

is a linear subspace, $1$ dimensional.

Theorem. In ${\bf R}^n$, given $X = (X_1,...X_n)$, let $S$ be the set of all vectors orthogonal to $X$. Then $S$ is a linear subspace.

Proof. Show that $S$ is closed under (1) addition & (2) scalar multiplication. First,

$u \in S$ iff $ = 0$.

1) Suppose $u,v \in S$. Re-write: $$ = 0, <v, X> = 0.$$

Add these, then by distributive law, $$\begin{array}{} &= \\ &= + <v, X> \\ &= 0 + 0 = 0, \end{array}$$

hence $$u + v \in S.$$

2) Suppose $u \in S$ and $\alpha \in {\bf R}$: $$ = 0 \rightarrow <\alpha u , X> = \alpha = \alpha \cdot 0 = 0. QED$$

Next, what is the dimension of $S$? Consider: $$S = \{y: <y, x> = 0 \}.$$

It is a solution set for a homogeneous linear equation.

Theorem. $${\rm dim \hspace{3pt}} S = n - 1,$$

i.e., $S$ is a hyperplane.

Review example. For a function $f \colon {\bf R}^2 \rightarrow {\bf R}$, the graph is typically a surface. This surface is a plane if this is a linear function. Suppose $$f(x) = f(x_1x_1) = 3x_1 + 4x_2.$$

We can interpret this as: $$\begin{array}{} f(x) = <(x_1x_2),(3,4)>, {\rm \hspace{3pt} or} \\ f(x) = <x,V> {\rm \hspace{3pt} where \hspace{3pt}} V = (3, 4), \\ ||V|| = (9 + 16)^{\frac{1}{2}} = 5. \end{array}$$

Prove: if $||x|| \leq 1$; then $|f(x)| \leq 5$.

$$|f(x)| = |<x, V>| \leq ||x||||V|| = ||x|| \cdot 5$$

by Cauchy-Schwarz inequality.

Example. Suppose $$Y = (2, 4, -1) and X =(x_1,x_2,x_3).$$

Then

$X \perp Y$ iff $2x_1 + 4x_2 - x_3= 0.$

The solution set S of the equation is the plane through the origin orthogonal to $Y =(2, 4, -1)$.

Example. Find a vector perpendicular to the plane $A$: $$x_1 - x_2 + 5x_3= 17.$$

Answer: $(1, -1, 5)$, just collecting the coefficients... Solution:

$v \perp A$ iff $v \perp S$, where $S$ is subspace given by

$$x_1 - x_2 + 5x_3= 0$$

(drop 17 from the above equation)

Interpret this equation as inner product: $$<X, (1, -1, 5)> = 0, {\rm \hspace{3pt} i.e}$$

$$X \perp (1, -1, 5), so v = (1, -1, 5).$$

The answer is not unique: $$u = (-1, 1, -5) = -v$$ $$u = 2v, 3v, -7v...$$

all work too.

Conclusion:

if $Q$ is the set of all vectors perpendicular to hyperplane $S$, then $Q = {\rm span}\{v \}$, a line through $0$, a $1$-dimensional subspace.

Example. If $$2x_1 - 12x_2 + 11x_3= 0$$

then $$v = (2, -12, 11).$$

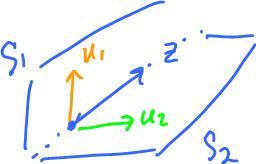
Example. Give a line spanned by vector $z$, represent it as the solution set of two linear equations. Analysis: $$S_1 \cap S_2 = {\rm span}\{z \}$$

$$u_2 {\rm \hspace{3pt} linear \hspace{3pt} independent \hspace{3pt} from \hspace{3pt}} z, u$$

Find them:

Pick $u_1$, not multiple of $z$.
Form subspace

$$S_1 = {\rm span}\{z, u_1 \},$$

Choose $u_2 \perp S_1$.
Form subspace

$$S_2 = {\rm span}\{z, u_2 \}.$$

Cross product

Problem. Given vectors $u, v \in {\bf R}^3$, find $w$ such that $u \perp w, v \perp w$.

Compare:

Scalar product $\alpha v \rightarrow w$, vector;
Inner product $ \rightarrow \alpha$ , scalar (aka dot product);
Cross product $u \times v \rightarrow w$, vector (aka vector product).

The last one is intended to solve the problem.

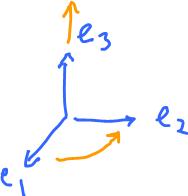
Observe: $$e_1 \times e_2 = e_3.$$

Here we turn from $e_1$ to $e_2$. Or the other way: $$e_2 \times e_1 = -e_3.$$

To come up with the general formula interpret the above results in terms of their coordinates by putting these three vectors in a $3 \times 3$ matrix:

Now, for $$u = (u_1 u_2 u_3), v= (v_1 v_2 v_3)$$

we define their "cross product" as $$u \times v = (u_2v_3- u_3v_2, u_3v_1 - u_1v_3, u_1v_2 - u_2v_1).$$

The coordinates of this new vector come from "cross multiplication" identical to the determinant of a $2 \times 2$ matrix of the coordinates of $u$ and $v$. In particular, consider

$$|u_1, u_2|$$

$$|v_1, v_2|$$

produces the third coordinate of $u \times v$. Meanwhile

$$|u_2, u_3|$$

$$|v_2, v_3|$$

produces the first coordinate of $u \times v$, etc. To verify this for the basis vectors: $$\begin{array}{} e_1 \times e_3 &= (1, 0, 0 \times (0, 0, 1) \\ &= (0 \cdot 1 - 0 \cdot 0, 0 \cdot 0 - 1 \cdot 1, 1 \cdot 0 - 0 \cdot 0) \\ &= (0, -1, 0) \\ &= -e_2. \end{array}$$

Algebraic Properties.

$u \times 0 = 0 \times v = 0$ (a vector)
$u \times v = -v \times u$ Anti-commutativity
$u \times (v + w) = u \times v + u \times w$ Distributivity
$\alpha (u + v) = (\alpha u) \times v$ Homogeneity

Geometric Properties. (1)$u \times v \perp u, u \times v \perp v.$

Indeed: $$\begin{array}{} &= <( u_2v_3- u_3v_2, u_3v_1 - u_1v_3, u_1v_2 - u_2v_1, u) \\ &= u_1u_2v_3- u_1u_3v_2 + u_2u_3v_1 -u_1u_2v_3+ u_1u_3v_2 - u_2u_3v_1 {\rm \hspace{3pt} Canceling \hspace{3pt} equal \hspace{3pt} terms} \\ &= 0 \end{array}$$

(2) $||u \times v|| = ||u|| \cdot ||v|| |sin \theta |$, where $\theta$ is the angle between $u$ and $v$. $\rightarrow$

(3) $u \times v = 0$ iff $u, v$ are multiples of each other.

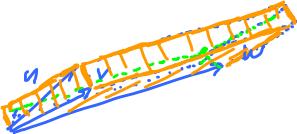
(4) $||u \times v||$ is the area of the parallelogram spanned by $u, v$.

(5) $||$ is the volume of the parallelepiped spanned by $u, v, w$.

No associativity: $$(u \times v)\times w \neq u \times(v \times w).$$

Example:

$$(e_1 \times e_2) \times e_2 \neq e_1 \times (e_2 \times e_2)$$

$$e_3\times e_2) \neq e_1 \times 0$$

$$e_1 \neq 0$$

Geometry of Euclidean space

Contents

The length of vectors, the norm

Angles between vectors

Projections of vectors

Projections on subspaces

Orthogonal vectors

Cross product

Navigation menu

Page actions

Page actions

Personal tools

Navigation

Search

Tools