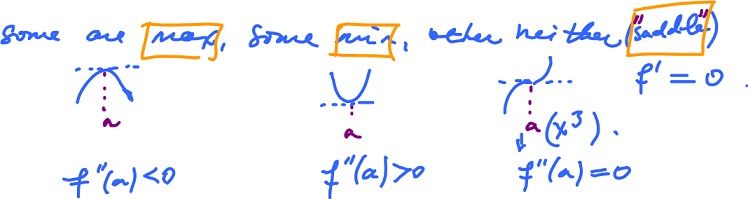First derivative test

First derivative test: classify the critical points based on change of the sign of f'(a)

   f′(x) > 0 for x < a and f′(x) < 0 for x > a,
   f′(x) < 0 for x < a and f′(x) > 0 for x > a,
   no change.

The gradient is used to find the extreme point of a function of several variable in a manner similar to the 1 dim case.

Theorem (First derivative test in dim n). Suppose a is a local extreme point of a differentiable function f. Then

 (1) f′(a) = 0,   
 (2) ∇f(a) = 0,
 (3) ∂f / ∂xi (a) = 0 for all i = 1, ..., n.

Exercise. Let f( x₁, x₂ ) = x₁² + x₂². Find the extrema. Solve the equations:

 ∂f / ∂x1 = 2x1 = 0 ⇒ x1 = 0,
 ∂f / ∂x2 = 2x2 = 0 ⇒ x2 = 0.

Hence the point ( 0, 0 ) is the only critical point of f (minimum).

Exercise. Let

 g( x1, x2 ) = x12 - x22. 

Then the calculation is the same as above, and we obtain ( 0, 0 ) as the only critical point (saddle).

Exercise. Let

 f = ( x1, x2 ) = x12.

Then

 ∂f / ∂x1 = 2x1 = 0 ⇒ x1 = 0,
 ∂f / ∂x2 = 0.

Hence the critical points are

 { ( 0, x2 ) : x2 ∈ ℝ }, 

which form a line.

Proof of the theorem. Suppose the point a is a maximum for f: ℝⁿ → ℝ. Suppose a = ( a₁, ..., a_n ). Consider

 f1: ℝ → ℝ, f1(x) = f( x1, a2, ..., an ),

which is differentiable. Then x = a₁ is a max of f₁. Now, by the First Derivative Test from Calc 1, we have

 f1′( a1 ) = 0.

This derivative is equal to the partial derivative:

 ∂f / ∂x1 (a) = 0.

Continue with f_k: ℝ → ℝ,

 fk(x) = f( a1 ... ak-1 × ak+1 ... an). 

Then f_k is differentiable, and x = a_k is a maximum. Find

 f′k (ak) = 0, 

so

 ∂f / ∂xk (a) = 0.

Thus all partial derivatives of f are equal to 0. Hence the gradient is zero too:

 ∇f(a) = 0   (a vector),

so

 f′(a) = 0  (a linear map). QED