Equilibria of dynamical systems

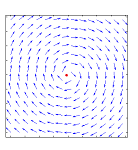
Recall that a discrete dynamical system is simply a map $F:S \to S$. Therefore the meaning of its equilibrium is simple: $F(a)=a$. It's a fixed point!

Let's illustrate this idea with an example outside the realm of physics, for a change. The application is to the existence of equilibria supply and demand in a simple market economy.

Suppose we have a "closed" market with $n+1$ commodities freely traded. Suppose that the possible prices $$p_0,p_1,...,p_n$$ of these commodities form a price vector $p$ at each time. And we assume that the prices are normalized: $$p_0+p_1+...+p_n=1.$$ Therefore the set of all possible price vectors is an $n$-simplex $S_n$ in the $(n+1)$-dimensional space.

We make a few assumptions.

First, we assume that the tomorrow's prices depend only on the today's prices. Then, indeed, we have a dynamical system of prices: $$X_{k+1}=F(X_k),$$ where $X_k \in S_n$ is the price vector at time $k$.

We need to justify this assumption. First, we can think of the market as truly "closed" so that there is no outside influence on the prices by world events, etc. We also think of the time gap as very short so that events like interest rate changes won't affect the prices. At the same time we have to think of the time gap as long enough for the information about price changes to disseminate to all participants.

Second, we assume that this dependence is continuous. In that case $F$ is a continuous map -- a self-map of a simplex! Therefore, it has a fixed point by the Brouwer fixed point theorem.

We need to justify the continuity assumption. This is how such a continuous $F$ can arise.

Suppose there are $N$ "agents" in the market, each owning a certain amount of each commodity. We suppose that

• $i$th agent owns $c_j^i$ of $j$th commodity.

These amounts form a vector $c^i$. Then his wealth is $w^i=<c^i,p>$, where $<,>$ is the dot product. We suppose also that this agent wants to own a different combination of commodities. This vector $d^i$ constitutes the demand of this agent. The demand, of course, depends on the current prices $p$.

One can argue now that the demand function $d^i=d^i(p)$ is continuous. The argument is based on the idea that the demand is elastic enough so that a small change in the price of a commodity will produce a small change in the person's demand for this commodity (or other commodities). We would have to ignore one-time purchases that require a certain threshold to be reached to become affordable. We can also argue that the person's desire for a certain commodity is unchanged but the affordability does change -- continuously -- with his wealth $w^i=<c^i,p>$ as the price vector $p$ changes.

It follows that the market-wide demand function $$d=\Sigma _i d^i$$ is continuous too. A separate argument can be made for the continuity of this function as an averaged demand of many people.

Now, the continuous demand will produce a continuous effect on the prices. Hence, $F$ is continuous.

So, there is a price vector that won't change and all trading will happen in a perfect harmony, forever.

It is important to notice here that, since the theorem holds for all maps homotopic to $F$, the result will hold under perturbations of $F$.

Of course this simple topological analysis won't tell us what this special combination of prices is, how many of these are possible, or whether one of them will be reached (or even approached) from the current state.

How does one incorporate other quantities into this oversimplified model?

For example, suppose the interest rates are to be included as they influence and are being influenced by the prices. The "state space" is then $S=S_n\times [0,R]$, where $S_n$ is our price simplex and $R$ is the largest possible interest rate. Then $S$ is homeomorphic to the $(n+1)$-simplex and, assuming continuity again, there is an equilibrium.

In general, any new quantity can be added to this model extending the state space $S$ via product. And there still be an equilibrium as long as

• the next value of this quantity is determined by the circumstances not time,
• this dependence is continuous, and
• the range of its values is a priori bounded.

The state space can be more complex than the simplex. For example, some of the combinations of prices may be impossible. Or new parameters are added that happen to be periodic in nature. In that case, more sophisticated tools, such as the Lefschetz number of $F$, may still detect equilibria.

What about continuous dynamical systems, i.e., systems that come as solution sets of ODEs?

One can use the uniqueness of solutions as well as continuous dependence on initial conditions of an ODE with a smooth right-hand side. Suppose we have such a (autonomous) system in a Euclidean space $S$. Now, suppose we are given a current state $a$ and a forward propagation time $t$. There is a unique solution to our ODE, $X_a=X_a(t)$, that satisfies $X_a(0)=a$. We define now the forward propagation map $Q:[0,\infty ]\times S\to S$ as: $$Q(t,a)=X_a(t).$$ It is a continuous map.

To detect equilibria of such a system one can construct a discrete system, as follows. For each specific forward propagation time $T$ we define: $$F_T(X)=Q(T,X),X\in S.$$ This is again a continuous function and, therefore, we have a discrete dynamical system. If $S$ is homeomorphic to the simplex, this system has an equilibrium, i.e., a state $E_T$ such that $F_T(E_T)=E_T$. But for our continuous system, this is a $T$-periodic state, i.e., a state $E_T$ such that there is a $T$-periodic solution $X(kT)=E_T$ for all $k=1,2...$. The limit $E_0$ of a sequence of these states as $T \to 0$ exists if $S$ is compact, and, under appropriate conditions, is also a solution of our system. This solution is an equilibrium in the sense of a constant map: $X(t)=E_0$ for all $t$.

The behaviors of solutions of ODEs are more limited than that of discrete systems. In particular, the forward propagation map built this way is homotopic to the identity map (Exercise). As a result, sometimes we can guarantee the existence of equilibria even if the state space $S$ isn't homeomorphic to the simplex. Observe that the Lefschetz number of the identity map is equal to the Euler characteristic of the space: $$\lambda_{Id_S}=\chi (S).$$ So, by the Lefschetz fixed point theorem there is a fixed point if $\chi (S)\ne 0$. This is true, in particular, for all even-dimensional spheres.

Exercise. What others?

Once again, since the Lefschetz fixed point theorem holds for all maps homotopic to $F$, the result is stable under perturbations.

Homotopy as a perturbation...

"Topology has the peculiarity that questions belonging to its domain may under certain circumstances be decidable even though the continua to which they are addressed may not be given exactly, but only vaguely, as is always the case in reality." -- H. Weyl, Philosophy of Mathematics and Natural Sciences, 1949.