This site is being phased out.
Duality: forms as cochains
Contents
Vectors and covectors
What is the relation between number $2$ and the “doubling” function $f(x)=2\cdot x$?
Linear algebra helps one appreciate this seemingly trivial relation. The answer is given by a linear operator, $${\bf R} \to \mathcal{L}({\bf R},{\bf R}),$$ from the reals to the vector space of all linear functions on the reals. In fact, it's an isomorphism!
More generally, suppose
- $R$ is a commutative ring, and
- $V$ is a finitely generated free module over $R$.
Definition. We let the dual module of $V$ to be $$V^* := \{\alpha :V \to R,\ \alpha \text{ linear}\}.$$
As the elements of $V$ are called vectors, those of $V^*$ are called covectors.
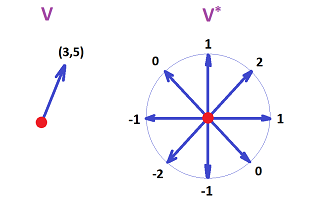
Example. An illustration of a vector in $v\in V={\bf R}^2$ and a covector in $u\in V^*$ is given below:
Here, a vector is just a pair of numbers, while a covector is a match of each unit vector with a number. The linearity of the latter is visible. $\square$
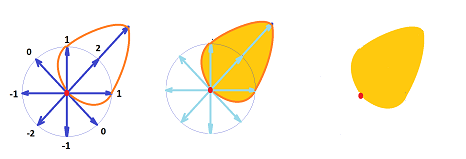
Exercise. Explain the alternative way a covector can be visualized as shown below. Hint: it resembles an oil spill.
Exercise. Prove that, if the spaces are finite-dimensional, we have $$\dim \mathcal{L}(V,U) = \dim V \cdot \dim U.$$
Example. In the above example, it is easy to see a natural way of building a vector $w$ from this covector $u$. Indeed, let's pick $w$ such that
- the direction of $w$ is that of the one that gives the largest value of the covector $u$ (i.e., $2$), and
- the magnitude of $w$ is that value of $u$. $\\$
So the result is $w=(2,2)$. Moreover, covector $u$ can be reconstructed from this vector $w$. $\square$
Exercise. What does this construction have to do with the norm of a linear operator?
In the spirit of this terminology, we might add “co” to any word to indicate its dual. Such is the relation between chains and cochains (forms). In that sense, $2$ is a number and $2x$ is a “conumber”, $2^*$.
Exercise. What is a “comatrix”?
The dual basis
Proposition. The dual $V^*$ of module $V$ is also a module, with the operations ($\alpha, \beta \in V^*,\ r \in R$) given by $$\begin{array}{llll} (\alpha + \beta)(v) &:= \alpha(v) + \beta(v),\ v \in V;\\ (r \alpha)(w) &:= r\alpha(w),\ w \in V. \end{array}$$
Exercise. Prove the proposition for $R={\bf R}$. Hint: start by indicating what $0, -\alpha \in V^*$ are, and then refer to theorems of linear algebra.
Below we assume that $V$ is finite-dimensional. Suppose also that we are given a basis $\{u_1, ...,u_n\}$ of $V$.
Definition. The dual vector $u_p^*\in V^*$ of vector $u_p\in V$ is defined by $$u_p^*(u_i):=\delta _{ip} ,\ i = 1, ...,n;$$ or $$u_p^*(r_1u_1+...+r_nu_n) = r_p.$$
Exercise. Prove that $u_p^* \in V^*$.
Definition. The dual of the basis $\{u_1, ...,u_n\}$ of $V$ is $\{u_1^*, ...,u_n^*\}$.
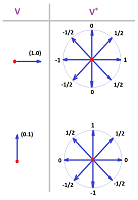
Example. The dual of the standard basis of $V={\bf R}^2$ is shown below:
$\square$
Let's prove that the dual of a basis is a basis. It takes two steps.
Proposition. The set $\{u_1^*, ...,u_n^*\}$ is linearly independent in $V^*$.
Proof. Suppose $$s_1u_1^* + ... + s_nu_n^* = 0$$ for some $r_1, ...,r_k \in R$. This means that $$s_1u_1^*(u)+...+s_nu_n^*(u)=0 ,$$ for all $u \in V$. For each $i=1, ...,n$, we do the following. We choose $u:=u_i$ and substitute it into the above equation: $$s_1u_1^*(u_i)+...+s_iu_i^*(u_i)+...+s_nu_n^*(u_i)=0.$$ Then we use $u_j^*(u_i)=\delta_{ij}$ to reduce the equation to: $$s_10+...+s_i1+...+s_n0=0.$$ We conclude that $s_i=0$. The statement of the proposition follows. $\blacksquare$
Proposition. The set $\{u_1^*, ...,u_n^*\}$ spans $V^*$.
Proof. Given $u^* \in V^*$, let's set $r_i := u^*(u_i) \in R,\ i=1, ...,n$. Now define $$v^* := r_1u_1^* + ... + r_nu_n^*.$$ Consider $$v^*(u_i) = r_1u_1^*(u_i) + ... + r_nu_n^*(u_i) = r_i.$$ So the values of $u^*$ and $v^*$ match for all elements of the basis of $V$. Accordingly, $u^*=v^*$. $\blacksquare$
Exercise. Find the dual of ${\bf R}^2$ for two different choices of bases.
Corollary. $$\dim V^* = \dim V = n.$$
Therefore, by the Classification Theorem of Vector Spaces, we have the following:
Corollary. $$V^* \cong V.$$
Even though a module is isomorphic to its dual, the behaviors of the linear operators on these two spaces aren't “aligned”, as we will show. Moreover, the isomorphism is dependent on the choice of basis.
The relation between a module and its dual is revealed if we look at vectors as column-vectors (as always) and covectors as row-vectors: $$V = \left\{x=\left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] \right\}, \quad V^* = \Big\{ y=[y_1, ...,y_n] \Big\} .$$ Then we can multiply the two as matrices: $$y\cdot x=[y_1, ...,y_n] \cdot \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] =x_1y_1+...+x_ny_n.$$
As before, we utilize the similarity to the dot product and, for $x\in V,y\in V^*$, represent $y$ evaluated at $x$ as $$\langle x,y \rangle:=y(x).$$ This isn't the dot product or an inner product, which is symmetric. It is called a pairing: $$\langle \cdot ,\cdot \rangle: V^*\times V \to R,$$ which is linear with respect to either of the components.
Exercise. Show that the pairing is independent of a choice of basis.
Exercise. When $V$ is infinite-dimensional with a fixed basis $\gamma$, its dual is defined as the set of all linear functions $\alpha:V\to R$ that are equal to zero for all but a finite number of elements of $\gamma$. (a) Prove the infinite-dimensional analogs of the results above. (b) Show how they fail to hold if we use the original definition.
The dual operators
Next, we need to understand what happens to a linear operator $$A:V \to W$$ under duality. The answer is uncomplicated but also unexpected, as the corresponding dual operator goes in the opposite direction: $$A^*:V^* \leftarrow W^*.$$ This isn't just because of the way we chose to define it: $$A^*(f):=f A;$$ a dual counterpart of $A$ can't be defined in any other way! Consider this diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & V & \ra{A} & W \\ & _{g \in V^*} & \searrow & \da{f \in W^*} \\ & & & R, \end{array} $$ where $R$ is our ring. If this is understood as a commutative diagram, the relation between $f$ and $g$ is given by the equation above. Therefore, we acquire $g$ from $f$ (by setting $g=fA$) and not vice versa.
Furthermore, the diagram also suggests that the reversal of the arrows has nothing to do with linearity. The issue is “functorial”.
We restate the definition in our preferred notation.
Definition. Given a linear operator $A:V \to W$, its dual operator $A^*:W^* \to V^*$, is given by $$\langle A^*g,v \rangle=\langle g,Av \rangle ,$$ for every $g\in W^*,v\in V$.
The behaviors of an operator and its dual are matched but in a non-trivial (dual) manner.
Theorem.
- (a) If $A$ is one-to-one, then $A^*$ is onto.
- (b) If $A$ is onto, then $A^*$ is one-to-one.
Proof. To prove part (a), observe that $\operatorname{Im}A$, just as any submodule in the finite-dimensional case, is a summand: $$W=\operatorname{Im}A\oplus N,$$ for some submodule $N$ of $W$. Consider some $f\in V^*$. Now, there is a unique representation of every element $w\in W$ as $w=w'+n$ for some $w'\in \operatorname{Im}A$ and $n\in N$. Therefore, there is a unique representation of every element $w\in W$ as $w=A(v)+n$ for some $v\in V$ and $n\in N$, since $A$ is one-to-one. Then we can define $g \in W^*$ by $\langle g,w \rangle:= \langle f,v \rangle$. Finally, we have: $$\langle A^*g,v \rangle =\langle g,Av \rangle=\langle g,w-n \rangle=\langle g,w \rangle-\langle g,n \rangle=\langle f,v \rangle+0=\langle f,v \rangle.$$ Hence, $A^*g=f$. $\blacksquare$
Exercise. Prove part (b).
Theorem. The matrix of $A^*$ is the transpose of that of $A$: $$A^*=A^T.$$
Exercise. Prove the theorem.
The compositions are preserved under the duality but in reverse:
Theorem. $$(BA)^*=A^*B^*.$$
Proof. Consider: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccc} & V & \ra{A} & W & \ra{B} & U\\ & _{g \in V^*} & \searrow &\quad\quad \da{f \in W^*} & \swarrow & _{h \in U^*} \\ \hspace{.27in}& & & R.&&&\hspace{.27in}\blacksquare \end{array}$$
Exercise. Finish the proof.
As you see, the dual $A^*$ behaves very much like, but not to be confused with, the inverse $A^{-1}$.
Exercise. When do we have $A^{-1}=A^T$?
The isomorphism between $V$ and $V^*$ is very straight-forward.
Definition. The duality isomorphism of the module $V$, $$D_V: V \to V^*,$$ is given by $$D_V(u_i):=u_i^*,$$ provided $\{u_i\}$ is a basis of $V$ and $\{u^*_i\}$ is its dual.
In addition to the compositions, as we saw above, this isomorphism preserves the identity.
Theorem. $$(\operatorname{Id}_V)^*=\operatorname{Id_{V^*}}.$$
Exercise. Prove the theorem.
Next, because of the reversed arrows, we can't say that this isomorphism “preserves linear operators”. Therefore, the duality does not produce a functor as we know it but rather a new kind of functor discussed later in this section.
Now, for $A:V \to U$ a linear operator, the diagram below isn't commutative: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllllllll} & V & \ra{A} & U \\ & \da{D_V} & \ne & \da{D_U} \\ & V^* & \la{A^*} & U^*\\ \end{array} $$
Exercise. Why not? Give an example.
Exercise. Show how a change of basis of $V$ affects differently the coordinate representation of vectors in $V$ and covectors in $V^*$.
However, the isomorphism with the second dual $$V^{**}:= (V^*)^*$$ given by $$D_{V^*}D_V:V\cong (V^*)^*$$ does preserve linear operators, in the following sense.
Theorem. The following diagram is commutative: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllll} & V & \ra{A} & U \\ & \da{D_V} & & \da{D_U} \\ & V^* & & U^*\\ & \da{D_{V^*}} & & \da{D_{U^*}} \\ & V^{**} & \ra{A^{**}} & U^{**}\\ \end{array} $$
Exercise. (a) Prove the commutativity. (b) Demonstrate that the isomorphism is independent of the choice of basis of $V$.
Our conclusion is that we can think of the second dual (but not the first dual) of a module as the module itself: $$V^{**}=V.$$ Same applies to the second duals of linear operators: $$A^{**}=A.$$
Exercise. Confirm that if we replace the dot product above with any choice of inner product (to be considered later), the duality theory presented above remains valid.
The cochain complex
A $k$-cochain on a cell complex $K$ is any linear function from the module of $k$-chains to $R$: $$s:C_k(K)\to R.$$ Then the chains are the vectors and the cochains are the corresponding covectors.
We use the duality theory we have developed to define the module of $k$-cochains as the dual of the module of the $k$-chains: $$C^k(K):=\Big( C_k(K) \Big)^*,$$
Further, the $k$th coboundary operator of $K$ is the dual of the $(k+1)$st boundary operator: $$\partial^k:=\Big( \partial _k \Big)^*:C^k\to C^{k+1}.$$
It is given by the Stokes Theorem: $$\langle \partial ^k Q,a \rangle := \langle Q, \partial_{k+1} a \rangle,$$ for any $(k+1)$-chain $a$ and any $k$-cochain $Q$ in $K$.
Theorem. The matrix of the coboundary operator is the transpose of that of the boundary operator: $$\partial^k=\Big( \partial_{k+1} \Big)^T.$$
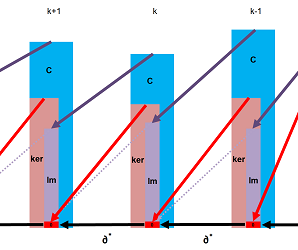
Definition. The elements in $Z^k:=\ker \partial ^* $ are called cocycles and the elements of $B^k:=\operatorname{Im} \partial^*$ are called coboundaries.
The following is a crucial result.
Theorem (Double Coboundary Identity). Every coboundary is a cocycle; i.e., for $k=0,1, ...$, we have $$\partial^{k+1}\partial^k=0.$$
Proof. It follows from the fact that the coboundary operator is the dual of the boundary operator. Indeed, $$\partial ^* \partial ^* = (\partial \partial)^* = 0^*=0,$$ by the double boundary identity. $\blacksquare$
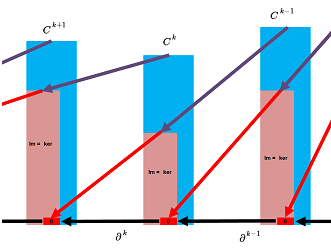
The cochain modules $C^k=C^k(K),\ k=0,1, ...$, form the cochain complex $\{C^*,\partial ^*\}$: $$\newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{rrrrrrrrrrr} 0& \la{0} & C^N & \la{\partial^{N-1}} & ... & \la{\partial^0} & C^0 &\la{0} &0 . \end{array} $$ According to the theorem, a cochain complex is a chain complex, just indexed in the opposite order.
Our illustration of a cochain complex is identical to that of the chain complex but with the arrows reversed:
Recall that a cell complex $K$ is called acyclic if its chain complex is an exact sequence: $$\operatorname{Im}\partial_k=\ker \partial_{k-1}.$$ Naturally, if a cochain complex is exact as a chain complex, it is also called exact:
Exercise. (a) State the definition of an exact cochain complex in terms of cocycles and coboundaries. (b) Prove that $\{C^k(K)\}$ is exact if and only if $\{C_k(K)\}$ is exact.
To see the big picture, we align the chain complex and the cochain complex in one, non-commutative, diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccccccccc} ...& \la{\partial^{k}} & C^k & \la{\partial^{k-1}} & C^{k-1} & \la{\partial^{k-1}} &... \\ ...& & \da{\cong} & \ne & \da{\cong} & &... \\ ...& \ra{\partial_{k+1}} & C_k & \ra{\partial_{k}} & C_{k-1} & \ra{\partial_{k}} & ... \end{array} $$
Exercise. (a) Give an example of a cell complex that demonstrates that the diagram doesn't have to be commutative. (b) What can you say about the chain complexes (and the cell complex) when this diagram is commutative?
Example (circle). Consider a cubical representation of the circle: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} \bullet& \ra{} & \bullet \\ \ua{} & & \ua{} \\ \bullet& \ra{} & \bullet \end{array} $$ Here, the arrows indicate the orientations of the edges -- along the coordinate axes. A $1$-cochain is just a combination of four numbers: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} \bullet& \ra{q} & \bullet \\ \ua{p} & & \ua{r} \\ \bullet& \ra{s} & \bullet \end{array} $$
First, which of these cochains are cocycles? According to our definition, they should have “horizontal difference - vertical difference” equal to $0$: $$(r-p)-(q-s)=0.$$ We could choose them all equal to $1$.
Second, what $1$-cochains are coboundaries? Here is a $0$-cochain and its coboundary: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} \bullet^1 & \ra{1} & \bullet^2 \\ \ua{1} & & \ua{1} \\ \bullet^0 & \ra{1} & \bullet^1 \end{array} $$ So, this $1$-form is a coboundary. But this one isn't: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} \bullet & \ra{1} & \bullet \\ \ua{1} & & \ua{-1} \\ \bullet & \ra{-1} & \bullet \end{array} $$ This fact is easy to prove by solving a little system of linear equations, or we can simply notice that the complete trip around the square adds up to $4$ not $0$. $\square$
Computing cochain complexes
Example (circle). We go back to our cubical complex $K$:
Consider the cochain complex of $K$: $$\newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} % \begin{array}{cccccccccccc} C^0& \ra{\partial^0}& C^1& \ra{\partial^1}& C^2 = 0. \end{array}$$ Observe that, due to $\partial ^1=0$, we have $\ker \partial^1 = C^1$.
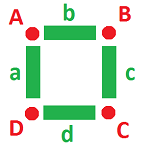
Let's list the bases of these vector spaces. Naturally, we start with the bases of the groups of chains $C_k$, i.e., the cells: $$\{A,B,C,D\},\ \{a,b,c,d\};$$ and then write their dual bases for the groups of cochains $C^k$: $$\{A^*,B^*,C^*,D^*\},\ \{a^*,b^*,c^*,d^*\};$$ They are given by $$A^*(A)=\langle A^*,A \rangle =1, ...$$
We find next the formula for $\partial^0$, a linear operator, which is its $4 \times 4$ matrix. For that, we just look at what happens to the basis elements:
$A^* = [1, 0, 0, 0]^T= \begin{array}{ccc} 1 & - & 0 \\ | & & | \\ 0 & - & 0 \end{array} \Longrightarrow \partial^0 A^* = \begin{array}{ccc} \bullet & -1 & \bullet \\ 1 & & 0 \\ \bullet & 0 & \bullet \end{array} = a^*-b^* = [1,-1,0,0]^T;$
$B^* = [0, 1, 0, 0]^T= \begin{array}{ccc}
0 & - & 1 \\
| & & | \\
0 & - & 0 \end{array} \Longrightarrow
\partial^0 B^* = \begin{array}{ccc}
\bullet & 1 & \bullet \\
0 & & 1 \\
\bullet & 0 & \bullet \end{array} = b^*+c^* = [0,1,1,0]^T;$
$C^* = [0, 0, 1, 0]^T= \begin{array}{ccc}
0 & - & 0 \\
| & & | \\
0 & - & 1 \end{array} \Longrightarrow
\partial^0 C^* = \begin{array}{ccc}
\bullet & 0 & \bullet \\
0 & & -1 \\
\bullet & 1 & \bullet \end{array} = -c^*+d^* = [0,0,-1,1]^T;$
$D^* = [0, 0, 0, 1]^T= \begin{array}{ccc}
0 & - & 0 \\
| & & | \\
1 & - & 0 \end{array} \Longrightarrow
\partial^0 D^* = \begin{array}{ccc}
\bullet & 0 & \bullet \\
-1 & & 0 \\
\bullet & -1 & \bullet \end{array} = -a^*-d^* = [-1,0,0,-1]^T.$
The matrix of $\partial^0$ is formed by the column vectors listed above: $$\partial^0 = \left[ \begin{array}{cccc} 1 & 0 & 0 & -1 \\ -1 & 1 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 1 & -1 \end{array} \right].$$
Now, from this data, we find the kernel and the image using the standard linear algebra.
The kernel is the solution set of the equation $\partial^0v=0$. It may be found by solving the corresponding system of linear equations with the coefficient matrix $\partial^0$ such as the Gaussian elimination (we can also notice that the rank of the matrix is $3$ and conclude that the dimension of the kernel is $1$).
The image is the set of $u$'s with $\partial^0v=u$. Once again, Gaussian elimination is an effective approach (we can also notice that the dimension of the image is the rank of the matrix, $3$). In fact, $$\operatorname{span} \Big\{\partial^0(A^*), \partial^0(B^*), \partial^0(C^*), \partial^0(D^*) \Big\} = \operatorname{Im} \partial^0 .$$ $\square$
Exercise. Compute the cochain complex of the T-shaped graph.
Exercise. Compute the cochain complex of the following complexes: (a) the square, (b) the mouse, and (c) the figure 8, shown below.
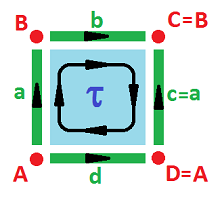
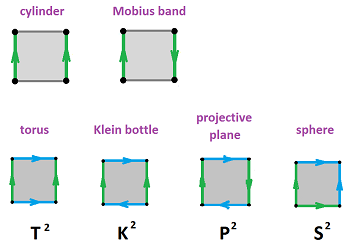
Example (cylinder). We build the cylinder $C$ via an equivalence relation of cells of the cell complex: $$a \sim c;\ A \sim D,\ B \sim C.$$
The chain complex is known, the cochain complex is derived, and the cohomology is computed accordingly: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} & & C_2 & \ra{\partial} & C_1 & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b,d > & \ra{?} & < A,B > \\ & & \tau & \mapsto & b - d \\ & & & & a & \mapsto & B-A \\ & & & & b & \mapsto & 0 \\ & & & & d & \mapsto & 0 \\ & & C^{2} & \la{\partial^*} & C^1 & \la{\partial^*} & C^0 \\ & & <\tau^*> & \la{?} & < a^*,b^*,d^* > & \la{?} & < A^*,B^* > \\ & & 0 & \leftarrowtail& a^* & & \\ & & \tau^* & \leftarrowtail& b^* & & \\ & & -\tau^* & \leftarrowtail& d^* & & \\ & & & & -a^* & \leftarrowtail & A^* \\ & & & & a^* & \leftarrowtail & B^* \\ {\rm kernels:} & & Z^2=<\tau^*> && Z^1=<a^*, b^*-d^* > & & Z^0=< A^*+B^* > \\ {\rm images:} & & B^2=<\tau^*> && B^1=< a^* > & & B^0 = < 0 > \end{array}$$ $\square$
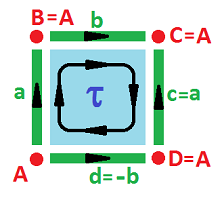
Example (Klein bottle). The equivalence relation on the complex of the square that gives ${\bf K}^2$ is: $$c \sim a,\ d \sim -b.$$
The chain complex is known, the cochain complex is derived, and the cohomology is computed accordingly: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{lccccccccccc} & & C_2 & \ra{\partial} & C_1 & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b > & \ra{?} & < A > \\ & & \tau & \mapsto & 2a \\ & & & & a & \mapsto & 0 \\ & & & & b & \mapsto & 0 \\ & & C^{2} & \la{\partial^*} & C^1 & \la{\partial^*} & C^0 \\ & & <\tau^*> & \la{?} & < a^*,b^* > & \la{?} & < A^* > \\ & & 2\tau^* & \leftarrowtail& a^* & & \\ & & 0 & \leftarrowtail& b^* & & \\ & & & & 0 & \leftarrowtail & A^* \\ {\rm kernels:} & & Z^2 = <\tau^*> && Z^1 = <b^*> & & Z^0 = < A > \\ {\rm images:} & & B^2 = <2\tau^*> && B^1 = 0 & & B^0 = 0 &\square \end{array}$$
Exercise. Show that $H^*({\bf K}^2;{\bf R})\cong H({\bf K}^2;{\bf R})$.
Exercise. Compute $H^*({\bf K}^2;{\bf Z}_2)$.
Exercise. Compute the cohomology groups of the rest of these surfaces:
Cochain maps
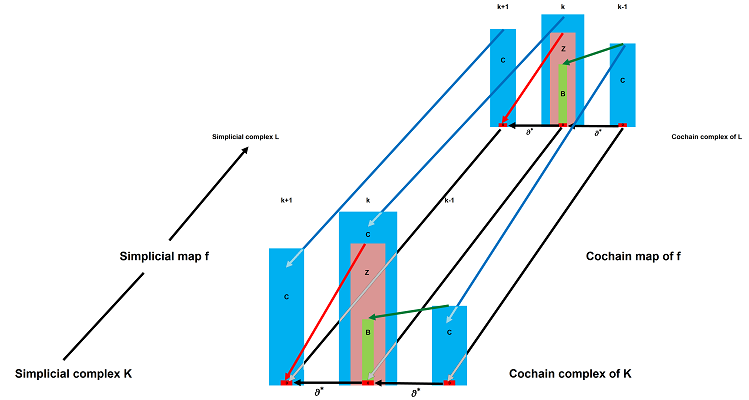
Our illustration of cochain maps is identical to the one for chain maps but with the arrows reversed:
The idea is the same: "These maps respect boundaries. The two constructions are also very similar and so are the results.
One can think of a function between two cell complexes $$f:K\to L$$ as one that preserves cells; i.e., the image of a cell is also a cell, possibly of a lower dimension: $$a\in K \Longrightarrow f(a) \in L.$$ If we expand this map by linearity, we have a map between (co)chain complexes: $$f_k:C_k(K) \to C_k(L)\ \text{ and } \ f^k:C^k(K) \leftarrow C^k(L).$$ What makes $f_k$ and $f^k$ continuous, in the algebraic sense, is that, in addition, they preserve (co)boundaries: $$f_k(\partial a)=\partial f_k(a)\ \text{ and } \ f^k(\partial^* s)=\partial^* f^k(s).$$ In other words, the (co)chain maps make these diagrams -- the linked (co)chain complexes -- commute: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccccccccc} \la{\partial} & C_k(K)\ & \la{\partial} & C_{k+1}(K)\ &\la{\partial} &\quad&\ra{\partial^*} & C ^k(K)\ & \ra{\partial^*} & C ^{k+1}(K)\ &\ra{\partial^*} \\ & \da{f_*} & & \da{f_*} &&\text{ and }&& \ua{f^*} & & \ua{f^*}\\ \la{\partial} & C_k(L) & \la{\partial} & C_{k+1}(L) & \la{\partial} &\quad& \ra{\partial^*} & C ^k(L) & \ra{\partial^*} & C ^{k+1}(L) & \ra{\partial^*} \end{array} $$
The following is obvious.
Theorem. The identity map induces the identity (co)chain map: $$(\operatorname{Id}_{|K|})_i = \operatorname{Id}_{C(K)}\ \text{ and } \ (\operatorname{Id}_{|K|})^i = \operatorname{Id}_{C^*(K)}.$$
This is what we derive from what we know about compositions of cell maps.
Theorem. The (co)chain map of the composition is the composition of the (co)chain maps $$(gf)_i = g_if_i\ \text{ and } \ (gf)^i = f^ig^i.$$
Notice the change of order in the latter case!
$$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccc} K & \ra{f} & L \\ & _{gf} \searrow\quad & \ \ \da{g} \\ & & M \end{array}\ \leadsto \ \begin{array}{rcrccccc} C(K) & \ra{f_*} & C(L) & &\\ & _{g_if_i} \searrow\quad\quad & \da{g_i}\\ & & C(M) \end{array} \text{and}\ \begin{array}{rcrccccc} C^*(K) & \la{f^*} & C^*(L) & &\\ & _{f^*g^*} \nwarrow\quad & \ua{g^*}\\ & & C^*(M) \end{array} $$
Theorem. Suppose $K$ and $L$ are cell complexes. If a map $$f : K \to L$$ is a cell map and a bijection, and $$f^{-1}: L \to K$$ is a cell map too, then the (co)chain maps $$f_k: C_k(K) \to C_k(L)\ \text{ and } \ f^k: C^k(K) \leftarrow C^k(L),$$ are isomorphisms for all $k$.
Corollary. Under the conditions of the theorem, we have: $$(f^{-1})_* = (f_*)^{-1}\ \text{ and } \ (f^{-1})^* = (f^*)^{-1}.$$
Theorem. If two maps are homotopic, they induce the same (co)chain maps: $$f \simeq g\ \Longrightarrow \ f_* = g_* \ \text{ and } \ f^* = g^*.$$
Computing cochain maps
We start with the most trivial examples and pretend that we don't know the answer...
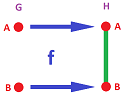
Example (inclusion). Suppose: $$G=\{A,B\},\ H=\{A,B,AB\},$$ and $$f(A)=A,\ f(B)=B.$$ This is the inclusion:
On the (co)chain level we have: $$\begin{array}{ll|ll} C_0(G)=< A,B >,& C_0(H)= < A,B >&\Longrightarrow C^0(G)=< A^*,B^* >,& C^0(H)= < A^*,B^* >,\\ f_0(A)=A,& f_0(B)=B & \Longrightarrow f^0=f_0^T=\operatorname{Id};\\ C_1(G)=0,& C_1(H)= < AB >&\Longrightarrow C^1(G)=0,& C^1(H)= < AB^* >\\ &&\Longrightarrow f^1=f_1^T=0. \end{array} $$ Meanwhile, $\partial ^0=0$ for $G$ and for $H$ we have: $$\partial ^0=\partial _1^T=[-1, 1].$$ Then, for $f^k:C^k(H)\to C^k(G),\ k=0,1$, we compute from the definition: $$\begin{array}{lllllll} f^0(A^*):=A^*, &f^0([B^*]):=B^* &\Longrightarrow f^0=[1,1]^T;\\ f^1=0&&\Longrightarrow f^1=0. \end{array} $$ The former identity indicates that $A$ and $B$ are separated if we reverse the effect of $f$. $\square$
Exercise. Modify the computation for the case when there is no $AB$.
Exercise. Compute the cochain maps for the following two two-edge simplicial complexes and these two simplicial maps: $$\begin{array}{llll} &K=\{A,B,C,AB,BC\},\ L=\{X,Y,Z,XY,YZ\};\\ \text{(a) }&f(A)=X,\ f(B)=Y,\ f(C)=Z,\ f(AB)=XY,\ f(BC)=YZ;\\ \text{(b) }&f(A)=X,\ f(B)=Y,\ f(C)=Y,\ f(AB)=XY,\ f(BC)=Y. \end{array}$$
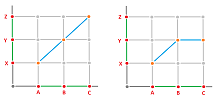
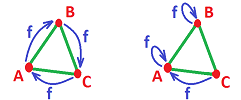
Example (rotation and collapse). Suppose we are given the following complexes and maps: $$G=H:=\{A,B,C,AB,BC,CA\} \text{ and }f(A)=B,\ f(B)=C,\ f(C)=A.$$ Here is a rotated triangle (left):
The cohomology maps are computed as follows: $$\begin{array}{lllll} f^1(AB^*+BC^*+CA^*)&=f^1(AB^*)+f^1(BC^*)+f^1(CA^*)\\ &=CA^*+AB^*+BC^*\\ &=AB^*+BC^*+CA^*. \end{array} $$ Therefore, the cochian map $f^1:C^1(H)\to C^1(G)$ is the identity.
Also (right) we collapse the triangle onto one of its edges: $$f(A)=A,\ f(B)=B,\ f(C)=A.$$ Then, $$\begin{array}{llllll} f^1(AB^*+BC^*+CA^*)&=f^1(AB^*)+f^1(BC^*)+f_1(CA^*)\\ &=(AB^*+CB^*)+0+0\\ &=2\partial^0(B^*). \end{array} $$ Therefore, the cochain map is zero. $\square$
Exercise. Provide the details of the computations.
Exercise. Modify the computation for the case (a) the map shown on the right, (b) a reflection and (c) a collapse to a vertex.