Directional derivative

When computing a limit, like

$$\lim_{x \rightarrow a}f(x),$$

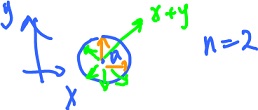
in dimension $1$, point a is "approached" by $x$. It can happen in a number of ways but from two directions only: left and right. In dimension $n$, there are infinitely many possible directions and $x$ can approach from any of them - if $a$ is an interior point of $D(f)$.

Let $n = 2$,

$$z = f( x, y ).$$

Then there are two main cases of how $z$ can approach some $a$:

• $z$ depends on $x$ only,
• $z$ depends on $y$ only.

These two cases lead to the concept of partial derivatives.

Let $n = 1$,

$$y = f(x),$$

then the derivative is the rate of change of $y$ with respect to $x$. We will use this concept initially to study the rates of change (corresponding to many possible directions) of functions of several variables.

We start with dimension $2$. In this low dimension, we can still visualize the function. In particular, the output $z$ can be treated as the altitude of a surface at the point $( x, y )$ on the plane.

Problem. Find the rate of change of $z$ as we move in a given direction to and from point $a$.

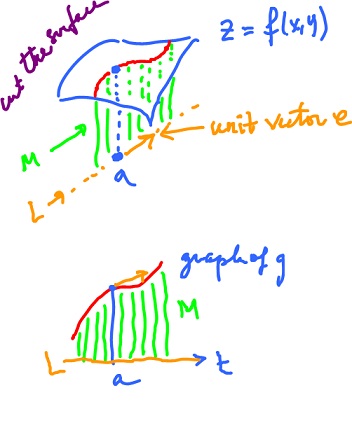
We approach the problem by creating a new function - a function of one variable. How? Take the graph

$$z = f(u), z {\in} {\bf R}, n {\in} {\bf R}^n, a {\in} {\bf R}^n.$$

Now choose a direction, a unit vector $e {\in} {\bf R}^n$ that follows the given direction. The point $a$ and the vector $e$ together define a line (a $1$-dimensional affine subspace) $L$:

$$u = a + te, t {\in} {\bf R}.$$

Consider

$$M = \{ ( u, z ): z {\in} {\bf R}, u {\in} L \} \subset {\bf R}^{n+1}.$$

$M$ is a plane, an affine subspace. Consider the intersection of the graph of $f$ and the plane $M$, the result is a curve (if $f$ is continuous). We will deal with a restriction of $f$ to $L, D(g) = L$. Now every element $v$ in $L$ has the form

$$u = a + te.$$

Define

$$g(t) = f( a + te ).$$

This is a function of one variable, t. Then $g′(t)$ is

$$g′(0) = \lim_{h \rightarrow 0} \frac{g( 0 + h ) - g(0)}{h},$$

which is the slope of the tangent line to the curve at this point.

Example. Let

$$f( x, y ) = x y, a = ( 1, 0 ), e = \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right),$$

further

$$L = \left\{ ( 1, 0 ) + t \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right): t {\in} {\bf R} \right\},$$

$$\begin{array}{} g(t) &= f( ( 1, 0 ) + t \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right) ) \\ &= f \left( 1 + \frac{t}{\sqrt{2}}, 0 + \frac{t}{\sqrt{2}} \right) \\ &= \left( 1 + \frac{t}{\sqrt{2}} \right) \cdot \left( \frac{t}{\sqrt{2}} \right)^2 \\ &= \left( 1 + \frac{t}{\sqrt{2}} \right) \cdot \frac{t^2}{2} \\ &= \frac{t^2}{2} + \frac{t^3}{2\sqrt{2}}, \end{array}$$

$$g′(t) = t + \frac{3}{2\sqrt{2}} t^2,$$

and

$$g′(0) = 0.$$

Definition. The directional derivative of $z = f(u)$ at $u = a$ in the direction of a unit vector $e$ is

$${\nabla}_e f(a) = \lim_{h \rightarrow 0} \frac{f(a+he)-f(a)}{h}.$$

Note 1: $\frac{f(a+he)-f(a)}{h}$ is a scalar function of $h$ from ${\bf R} {\rightarrow} {\bf R}$.

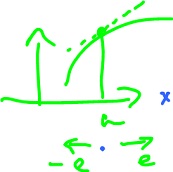
Note 2: if $k = -h$, then

$$\lim_{k \rightarrow 0} \frac{f( a + ke ) - f(a)}{-k} = - {\nabla}_e f(a).$$

So

$${\nabla}_e f(a) = -{\nabla}_{-e} f(a)$$

Indeed, consider an example in dimension $1$:

$${\nabla}_{-1} x^2 |_{x=1} = \lim_{h \rightarrow 0} \frac{( 1 + h(-1) )^2 - 1^2}{h}$$

and

$$( x^2 )′ |_{x=1} = {\nabla}_1 x^2 |_{x=1} = lim_{h \rightarrow 0} \frac{( 1 + h - 1 )^2 - 1^2}{h}.$$

Example.

$$\begin{array}{} \lim_{h \rightarrow 0} \frac{1}{h} ( f( ( 1, 0 ) + h ( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} ) ) - f( 1, 0 ) ) &=\lim_{h \rightarrow 0} \frac{1}{h} ( f( ( 1 + \frac{h}{\sqrt{2}}, \frac{h}{\sqrt{2}} ) ) - f( 1, 0 ) ) \\ &=\lim_{h \rightarrow 0} \frac{1}{h} ( ( 1 + \frac{h}{\sqrt{2}} )( \frac{h}{\sqrt{2}} )^2 ) - 0 ) \\ &=\lim_{h \rightarrow 0} ( 1 + \frac{h}{\sqrt{2}} ) \frac{h}{2} \\ &= 0. \end{array}$$

Example. Consider

$$f( x_1, x_2 ) = 1 - 2x_1 + 3x_2$$

at $a = ( 2, -1 )$. Find the directional derivative "in the direction" of $v = ( 3, 4 )$.

You can't use $u$ as the direction as the direction has to be a unit vector. So, find $e$ first:

$$e = \frac{v}{|| v ||} = - \frac{( 3, 4 )}{( 3^2 + 4^2 )^{\frac{1}{2}}} = ( \frac{3}{5}, \frac{4}{5} ).$$

Finish..