Differentiation without limits: part 3

Next operation is division...

Quotient Rule. $$\frac{d}{dx} \left(\frac{u}{v}\right) = \dfrac{\dfrac{du}{dx}\cdot v – \dfrac{dv}{dx}\cdot u}{v^{2}}$$ The formula is similar to the Product Rule in the sense that this again involves "cross-multiplication".

Example:

Find $ \left( \frac{\sqrt{x}}{x^{2} + 1} \right)^{\prime}.$ Consider: $$ \begin{aligned} u & = \color{maroon}{\sqrt{x}} \to \frac{du}{dx} = \color{green}{\frac{1}{2\sqrt{x}}} \\ v & = \color{green}{x^{2} + 1} \to \frac{dv}{dx} = \color{maroon}{2x} \end{aligned} $$ where $$ \frac{d}{dx} \left(\frac{u}{v}\right) = \frac{\color{green}{\dfrac{1}{2\sqrt{x}}(x^{2} + 1)} - \color{maroon}{\sqrt{x}\cdot 2x}}{( x^{2} + 1)^{2}} $$ (You don't have to simplify.)

Exercise:

$$ \begin{aligned} \left(\frac{A}{B + C e^{x}}\right)^{\prime} & = ?? \text{Quotient rule first?} \\ \frac{d}{dx}\left(\frac{A}{B + Ce^{x}}\right) & = ?? \end{aligned} $$ Prepare all the derivatives you'll need $$ \begin{aligned} (A)^{\prime} & = 0 \\ (B + Ce^{x})^{\prime} & \overset{\text{SR}}{=} (B)^{\prime} + (Ce^{x})^{\prime} \\ & \overset{\text{CMR}}{=} 0 + C(e^{x})^{\prime} \\ & = Ce^{x} \qquad \text{(formula)} \end{aligned} $$

Quotient Rule next: $$ \begin{aligned} \left(\frac{A^{\prime}}{B + C e^{x}}\right)^{\prime} & = \frac{A^{\prime}(B + Ce^{x}) – A(B + Ce^{x})^{\prime}}{(B + C e^{x})^{2}} \\ & \text{Substitute} \\ & = \frac{0(B + Ce^{x}) – A\cdot Ce^{x}}{(B + C e^{x})^{2}} \\ & = \frac{-ACe^{x}}{(B + Ce^{x})^{2}}. \end{aligned} $$

Now trigonometric functions...

Start with this plan:

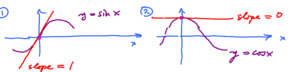
1. Derivative of $\sin$ at 0, find $(\sin x)^{\prime}$.
2. Derivative of $\cos$ at 0, find $(\cos x)^{\prime}$.

Trignometric Functions.

$$ \begin{aligned} (\sin x)^{\prime} & = \lim_{h \to 0} \frac{\sin( x + h) – \sin x}{h} \text{addition formula} \\ & = \lim{h \to 0} \frac{\sin x \cos h + \cos x \sin h – \sin x}{h} \\ & = \lim_{h \to 0} \frac{\sin x \cos h – \sin x}{h} + \cos x \cdot \frac{\sin h}{h} \\ & = \lim_{h \to 0} \frac{\sin x \cos h – \sin x}{h} + \cos x \frac{\sin h}{h} \\ & \overset{\text{SR}}{=} \lim_{h \to 0} \sin x \frac{\cos h – 1}{h} + \lim_{h \to 0} \cos x \frac{\sin h}{h} \\ & = \sin x \underbrace{\lim_{h \to 0} \frac{\cos h - 1}{h}}_{\text{Recognize these limits!}} + \cos x \underbrace{\lim_{h \to 0} \frac{\sin h – 0}{h}}_{\text{These are derivatives of what?}} \\ & = \sin x \lim_{h \to 0} \frac{\cos h – \cos 0}{h} + \cos x \lim_{h \to 0}\frac{\sin h – \sin 0}{h} \end{aligned} $$

Recall the definition: $$f^{\prime}(a) = \lim_{h \to 0} \frac{f(a + h) - f(a)}{h} $$ and match the terms. So, in the above two limits, we choose respectively:

1. $f(x) = \cos x, a = 0$.
2. $f(x) = \sin x, a = 0$.

Therefore we can re-write the expression as $$= \sin x [\text{the derivative of } \cos x \text{ at } a = 0) + \cos x [\text{the derivative of } \sin x \text{ at } a = 0).$$ What are they equal to?

1. this derivative is 1,
2. this derivative is 0.

So, $$ = \sin x \cdot 0+ \cos x \cdot 1 $$ $$= \cos x $$ or $$ (\sin x)^{\prime} = \cos x $$

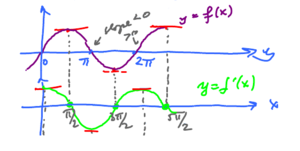
Let's confirm the answer graphically, how? By plotting the derivative of sine based entirely on its graph.

Graphical plots of derivatives.

This looks like $\cos x$!

Let's differentiate one more time, graphically again. Plot its derivative below.

Graphical Plot of Second Derivative.

Yes, $(\cos x)^{\prime} = -\sin x.$

Example:

$$ \begin{aligned} (\sin x e^{x})^{\prime} = (\sin x)^{\prime} e^{x} + \sin x \cdot (e^{x})^{\prime} \\ & = \cos x e^{x} + \sin x e^{x} \\ & = e^{x}(\cos x + \sin x) \end{aligned} $$ Further, $$\begin{aligned} (\sin x)^{\prime} & = \cos x \\ (\cos x)^{\prime} & = -\sin x \\ (-\sin x)^{\prime} & = -\cos x \\ (-\cos x)^{\prime} & = \sin x \end{aligned} $$ or $$ (\sin x )^{\prime\prime\prime\prime} = \sin x $$ (That's 4th derivative.) We are back where we started!

The differentiation process is cyclic!

Let's compare to other functions:

1. $$(x^{n})^{\prime} = nx^{n-1}.$$ Power decreases at first. Then, $(x^{n})^{ n+1} = 0$. So it stays 0.

2. $$\begin{aligned} (e^{x})^{\prime} & = e^{x} \\ (e^{x})^{(n)} & = e^{x}\end{aligned}$$ Constant!

3. $$\begin{aligned}(\sin x)^{(4n)} & = \sin x \\(\cos x)^{(4n)} & = \cos x\end{aligned}$$ Cyclic!

4. $$\begin{aligned}(x^{n})^{\prime} & = nx^{(n-1)}, \quad n = -1,-2 \\(x^{-1})^{\prime} & = -1x^{-2} \\(-x^{-2})^{\prime} & = 2x^{-3}\end{aligned}$$ So power goes to $–\infty$.

More $$\begin{aligned} (\tan x)^{\prime} & = (\frac{\sin x}{cos x})^{\prime} \overset{\text{QR}}{=} \frac{(\sin x)^{\prime} \cos x – \sin x (\cos x)^{\prime}}{(\cos x)^{2}} \\ & = \frac{\cos x \cos x – \sin x (-\sin x)}{cos^{2} x} \\ & = \frac{\cos^{2}x + \sin^{2}x}{\cos^{2}x} \quad \text{Pythagorean Theorem} \\ & = \sec^{2}x \end{aligned} $$ (9 formulas to know so far)
One algebraic operation is missing? Composition!

Continue to Differentiation without limits: part 4.