This site is being phased out.
Differential forms: exam 1 discussion
1. Simplify: $$(a)\, 2dxdydz+3dydxdz-dydxdz,$$ $$(b)\, (x¹dx²+x²dx²)(x²dx¹dx²+x²dx¹dx³+x¹dx²dx³).$$ (a) Compute the exterior derivative of the following discrete differential 1-form in R²:
... ⋅ 0 ⋅ 0 ⋅ 0 ⋅ ... ... -1 0 1 2 ... ... ⋅ -1 ⋅ 0 ⋅ 1 ⋅ ... ... -1 0 1 2 ... ... ⋅ 0 ⋅ 0 ⋅ 0 ⋅ ...
(b) Is this form exact?
2. Prove that $dx_{i₁}...dx_{i_{k}}=0$ if and only if $i_{s}=i_{r}$ for some $s≠r$.
3.(a) Define discrete differential forms for the triangular grid on the plane. (b) Define the exterior derivative of 0- and 1-forms and prove that $dd=0$.
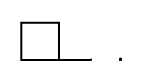
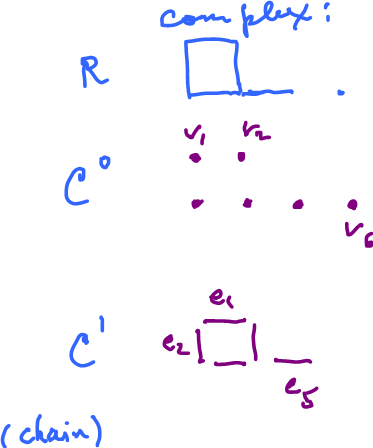
4. (a) Describe the vector spaces of discrete differential forms for the complex below:
(b) Evaluate the cohomology of the complex (just the answer).
5. (a) Given a smooth function $F:R→R$, what happens to the forms $1,dx$ under $F$? Hint: you can think of F as a change of variables. (b) Given a smooth function $F:R²→R²$, what happens to the forms $1,dx,dy,dxdy$ under $F$? (c) Given a function $F:R₁→R₂$, what kind of function does $F$ generate between $Ω^{k}(R₁)$ and $Ω^{k}(R₂)$?
Discrete forms:
Basis of the $0$-form: $\varphi_1, \ldots, \varphi_6$ defined byt $\varphi_1(v_j) = \delta_{ij}$
Basis of the $1$-form: $\psi_1, \ldots, \psi_5$ defined by $\psi_i(\varphi_j) = \delta_{ij}$.
$C^2 = 0$
Co-homology: $H^0 = {\bf R}^2$, $H^1 = {\bf R}$, $H^2 = 0$, etc.
#6: $F \colon {\bf R} \rightarrow {\bf R}$ smooth. ($1 \rightarrow ?$ and $dx \rightarrow ?$)
$y = F(x)$ $\leftarrow F(dx)?$