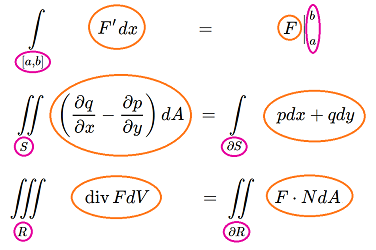This site is being phased out.
Cubical calculus
Contents
Calculus and cochains
Suppose $I$ is a closed interval. In the analysis context, the definite integral -- with the interval of integration fixed -- is often thought of as a real-valued function of the integrand. This idea is revealed in the usual function notation: $$G\big( f \big):= \displaystyle\int_I f(x) dx \in {\bf R}.$$ This point of view is understandable: after all, the Riemann integral is introduced in calculus as the limit of the Riemann sums of $f$. The student then discovers that this function is linear: $$G \big( sf+tg \big)=sG\big( f \big) +tG \big( g \big) ,$$ with $s,t\in {\bf R}$. However, this notation might obscure another important property of integral, the additivity: $$\displaystyle\int_{[a,b]\cup [c,d]} f(x) dx = \displaystyle\int_{[a,b]} f(x) dx+ \displaystyle\int_{[c,d]} f(x) dx,$$ for $a < b \le c < d$. We then realize that we can also look at the integral as a function of the interval -- with the integrand fixed -- as follows: $$H \big( I \big) := \displaystyle\int_I f(x)dx.$$
In higher dimensions, the intervals are replaced with surfaces and solids while the expression $f(x)dx$ is replaced with $f(x,y)dxdy$ and $f(x,y,z)dxdyz$, etc. These “expressions” are called differential forms and each of them determines such a new function. That's why we further modify the notation as follows: $$\omega \big( I \big) =\displaystyle\int_I \omega.$$ This is an indirect definition of a differential form of dimension $1$ -- it is a function of intervals. Moreover, it is a function of $1$-chains such as $[a,b]+[c,d]$. We can see this idea in the new form of the additivity property: $$\omega \big( I+J \big) = \omega \big( I \big) + \omega \big( J \big).$$ We recognize this function as a $1$-cochain!
In light of this approach, let's take a look at the integral theorems of vector calculus. There are many of them and, with at least one for each dimension, maybe too many...
Let's proceed from dimension $3$, look at the formulas, and see what they have in common.
Green's Theorem: $$\displaystyle \iint_{S} \left( \frac{\partial q}{\partial x} - \frac{\partial p}{\partial y} \right) dA = \displaystyle\int_{\partial S} p dx + q dy. $$
Here, the integrals' domains are a solid and its boundary surface respectively.
Gauss' Theorem: $$\displaystyle \iiint_{R} \operatorname{div}F dV = \displaystyle \iint_{\partial R} F \cdot N dA.$$
The domains of integration are a plane region and its boundary curve.
Fundamental Theorem of Calculus: $$\displaystyle\int_{[a,b]} F' dx = F \Big|_{a}^b.$$
In the left-hand side, the integrand is $F' dx$. We think of the right-hand side as an integral too: the integrand is $F$. Then the domains of integration are a segment and its two endpoints: $$[a,b] \text{ and } \{a, b\}= \partial [a,b].$$
What do these three have in common?
Setting aside possible connections between the integrands, the pattern of the domains of integration is clear. The relation is the same in all these formulas:
Now, there must be some kind of a relation for the integrands too. The Fundamental Theorem of Calculus suggests a possible answer:
Clearly, for the other two theorems, this simple relation can't possibly apply. We can, however, make sense of this relation if we treat those integrands as differential forms. Then the form on the left is what we call the exterior derivative of the form on the right. Consequently, the theorem can be turned into a definition of this new form.
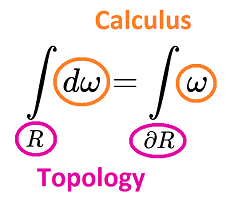
Thus, we have just one general formula which includes all three (and many more):
Stokes Theorem: $$\displaystyle\int_R d \omega = \displaystyle\int_{\partial R} \omega.$$
The relation between $R$ and $\partial R$ is a matter of topology. The relation between $d \omega$ and $\omega$ is a matter of calculus, the calculus of differential forms:
Furthermore, as we shall see, the transition from topology to calculus is just algebra!
Visualizing cubical cochains
In calculus, the quantities to be studied are typically real numbers. We choose our ring of coefficients to be $R={\bf R}$.
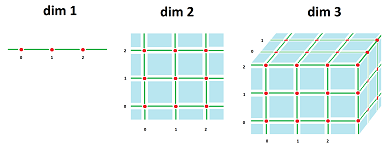
Meanwhile, the locus is typically the Euclidean space ${\bf R}^n$. We choose for now to concentrate on the cubical grid, i.e., the infinite cubical complex acquired by dividing the Euclidean space into cubes, ${\mathbb R}^n$.
In ${\mathbb R}^1$, these pieces are: points and (closed) intervals,
- the $0$-cells: $...,\ -3,\ -2, \ -1, \ 0, \ 1, \ 2, \ 3, \ ...$, and
- the $1$-cells: $...,\ [-2,-1], \ [-1,0],\ [0,1], \ [1,2], \ ...$.
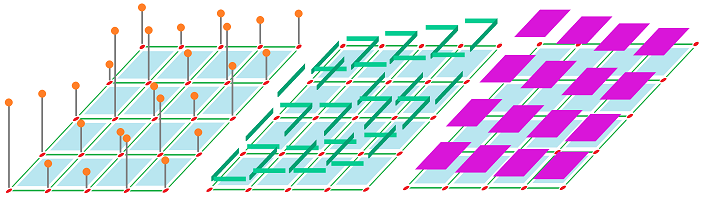
In ${\mathbb R}^2$, these parts are: points, intervals, and squares (“pixels”):
Moreover, in ${\mathbb R}^2$, we have these cells represented as products:
- $0$-cells: $\{(0,0)\}, \{(0,1)\}, ...;$
- $1$-cells: $[0,1] \times \{0\}$, $\{0\} \times [0,1], ...;$
- $2$-cells: $[0,1] \times [0,1], ....$
Recall that within each of these pieces, a cochain is unchanged; i.e., it's a single number.
Then, the following is the simplest way to understand these cochains.
Definition. A cubical $k$-cochain is a real-valued function defined on $k$-cells of ${\mathbb R}^n$.
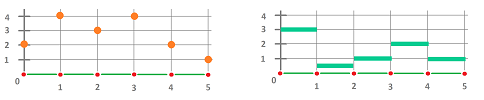
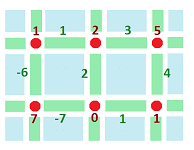
This is how we plot the graphs of cochains in ${\mathbb R}^1$:
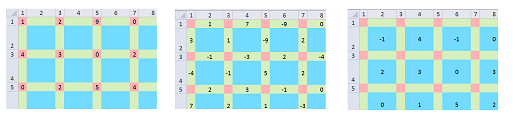
And these are $0$-, $1$-, and $2$-cochains in ${\mathbb R}^2$:
To emphasize the nature of a cochain as a function, we can use arrows:
Here we have two cochains:
- a $0$-cochain with $0\mapsto 2,\ 1\mapsto 4,\ 2\mapsto 3, ...$; and
- a $1$-cochain with $[0,1]\mapsto 3,\ [1,2]\mapsto .5,\ [2,3]\mapsto 1, ...$.
A more compact way to visualize is this:
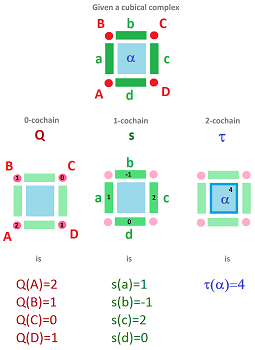
Here we have two cochains:
- a $0$-cochain $Q$ with $Q(0)=2,\ Q(1)=4,\ Q(2)=3, ...$; and
- a $1$-cochain $s$ with $s\Big([0,1] \Big)=3,\ s\Big([1,2] \Big)=.5,\ s\Big([2,3] \Big)=1, ...$.
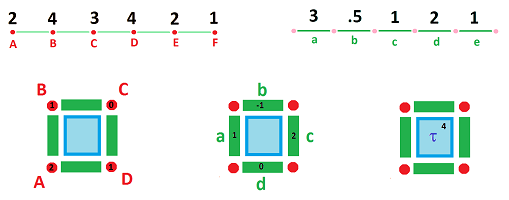
We can also use letters to label the cells, just as before. Each cell is then assigned two symbols: one is its name (a latter) and the other is the value of the cochain at that location (a number):
Here we have:
- $Q(A)=2,\ Q(B)=4,\ Q(C)=3, ...$;
- $s(AB)=3,\ s(BC)=.5,\ s(CD)=1, ...$.
We can simply label the cells with numbers, as follows:
Exercise. Another way to visualize cochains is with color. Implement this idea with a spreadsheet.
Cochains as integrands
It is common for a student to overlook the distinction between chains and cochains and to speak of the latter as linear combinations of cells. The confusion is understandable because they “look” identical. Frequently, one just assigns numbers to cells in a complex as we did above. The difference is that these numbers aren't the coefficients of the cells in some chain but the values of the $1$-cochain on these cells. The idea becomes explicit when we think in calculus terms:
- cochains are integrands, and
- chains are domains of integration.
In the simplest setting, we deal with the intervals in the complex of the real line ${\mathbb R}$. Then the cochain assigns a number to each interval to indicate the values to be integrated and the chain indicates how many times the interval will appear in the integral, typically once:
Here, we have: $$\begin{array}{lllllllll} h(a)&= \displaystyle\int _a h \\ &=\displaystyle\int _{[0,1]} h &+ \displaystyle\int _{[1,2]} h &+\displaystyle\int _{[2,3]} h &+\displaystyle\int _{[3,4]} h&+\displaystyle\int _{[4,5]} h\\ &=3&+.5&+1&+2&+1. \end{array}$$
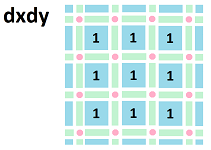
The simplest cochain of this kind is the cochain that assigns $1$ to each interval in the complex ${\mathbb R}$. We call this cochain $dx$. Then any cochain $h$ can be built from $dx$ by multiplying -- cell by cell -- by a discrete function that takes values $3,.5,1,2,1$ on these cells:
The main property of this new cochain is: $$\displaystyle\int _{[A,B]}dx=B-A.$$
Exercise. What is the antiderivative of $dx$?
Exercise. Show that every $1$-cochain in ${\mathbb R}^1$ is a “multiple” of $dx$: $h=Pdx$.
Next, ${\mathbb R}^2$:
In the diagram,
- the names of the cells are given in the first row;
- the values of the cochain on these cells are given in the second row; and
- the algebraic representation of the cochains is in the third. $\\$
The second row gives one a compact representation of the cochain when you don't want to name the cells.
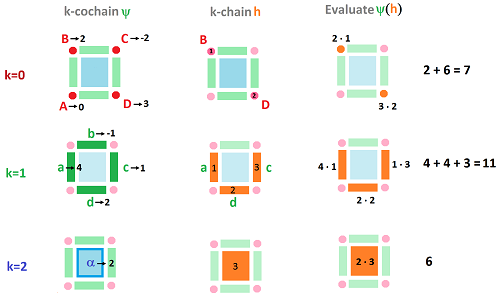
Cochains are real-valued, linear functions defined on chains:
One should recognize the second line as a line integral: $$\psi (h)= \displaystyle\int _h \psi .$$
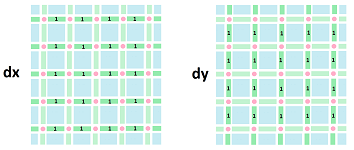
What is $dx$ in ${\mathbb R}^2$? Naturally, its values on the edges parallel to the $x$-axis are $1$'s and on the one parallel to the $y$-axis are $0$'s:
Of course, $dy$ is the exact opposite. Algebraically, their representations are as follows:
- $dx\Big([m,m+1]\times \{n\}\Big)=1,\ dx\Big(\{m\} \times [n,n+1] \Big)=0$;
- $dy\Big([m,m+1]\times \{n\}\Big)=0,\ dy\Big(\{m\} \times [n,n+1] \Big)=1$.
Now we consider a general $1$-cochain: $$P dx + Q dy,$$ where $P,Q$ are discrete functions, not just numbers, that may vary from cell to cell. For example, this could be $P$:
Exercise. Show that every $1$-cochain in ${\mathbb R}^2$ is such a “linear combination” of $dx$ and $dy$.
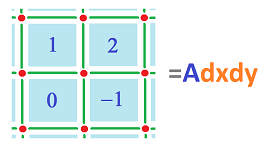
At this point, we can integrate this cochain. As an example, suppose $S$ is the chain that represents the $2\times 2$ square in this picture going clockwise. The edges are oriented, as always, along the axes. Let's consider the line integral computed along this curve one cell at a time starting at the left lower corner: $$\displaystyle\int _S Pdx = 0\cdot 0 + 1\cdot 0 + (-1)\cdot 1 + 1\cdot 1 + 0\cdot 0 + 2\cdot 0 + 3\cdot (-1) + 1\cdot (-1).$$ We can also compute: $$\displaystyle\int _S Pdy = 0\cdot 1 + 1\cdot 1 + (-1)\cdot 0 + 1\cdot 0 + 0\cdot (-1) + 2\cdot (-1) + 3\cdot 0 + 1\cdot 0.$$ If $Q$ is also provided, the integral $$\displaystyle\int _S Pdx+Qdy$$ is a similar sum.
Next, we illustrate $2$-cochains in ${\mathbb R}^2$:
The double integral over this square, $S$, is $$\displaystyle\int _S Adxdy = 1+2+0-1=2.$$ And we can understand $dx \hspace{1pt} dy$ as a $2$-cochain that takes the value of $1$ on each cell:
Exercise. Evaluate $\int_S dxdy$, where $S$ is an arbitrary collection of $2$-cells.
The algebra of cochains
We already know that the cochains, as cochains, are organized into vector spaces, one for each degree/dimension. Let's review this first.
If $p,q$ are two cochains of the same degree $k$, it is easy to define algebraic operations on them.
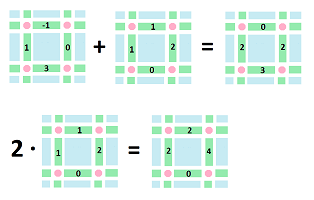
First, their addition. The sum $p + q$ is a cochain of degree $k$ too and is computed as follows: $$(p+q)(a) := p(a) + q(a),$$ for every $k$-cell $a$.
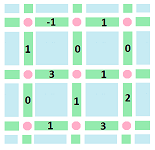
As an example, consider two $1$-cochains, $p,q$. Suppose these are their values defined on the $1$-cells (in green):
Then $p+q$ is found by $$1+1=2,\ -1+1=0,\ 0+2=2,\ 3+0=3,$$ as we compute the four values of the new cochain one cell at a time.
Next, scalar multiplication is also carried out cell by cell: $$(\lambda p)(a) := \lambda p(a), \ \lambda \in {\bf R},$$ for every $k$-cell $a$.
We know that these operations satisfy the required properties: associativity, commutativity, distributivity, etc. Subsequently, we have a vector space: $$C^k=C^k({\mathbb R}^n),$$ the space of $k$-cochains on the cubical grid of ${\bf R}^n$.
There is, however, an operation on cochains that we haven't seen yet.
Can we make $dxdy$ from $dx$ and $dy$? The answer is provided by the wedge product of cochains: $$dxdy=dx\wedge dy.$$ Here we have:
- a $1$-cochain $dx \in C^1({\mathbb R}_x)$ defined on the horizontal edges,
- a $1$-cochain $dy \in C^1({\mathbb R}_y)$ defined on the vertical edges, and
- a $2$-cochain $dxdy \in C^2({\mathbb R}^2)$ defined on the squares. $\\$
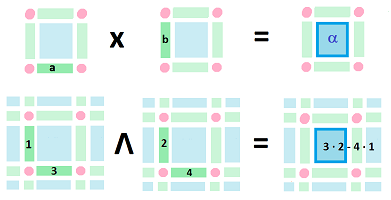
But squares are products of edges: $$\alpha=a \times b.$$ Then we simply set: $$(dx\wedge dy) (a\times b):=dx(a)\cdot dy(b).$$ What about $dydx$? To match what we know from calculus: $$\displaystyle\int _\alpha dy dx=-\displaystyle\int_\alpha dxdy,$$ we require anti-commutativity of cubical cochains under wedge products: $$dy\wedge dx =-dx\wedge dy.$$
Now, suppose we have two arbitrary $1$-cochains $p,q$ and we want to define their wedge product on the square $\alpha:= a\times b$. We can't use the simplest definition: $$(p \wedge q)(a \times b) \stackrel{?}{=} p(a) \cdot q(b) ,$$ as it fails to be anti-commutative: $$(q \wedge p)(a \times b) = q(a) \cdot p(b) = p(b) \cdot q(a).$$ Since we need both of these terms: $$p (a) q(b) \quad p (b) q(a),$$ let's combine them.
Definition. The wedge product of two $1$-cochains is a $2$-cochain given by $$(p \wedge q)(a \times b):=p (a) q(b) - p (b) q(a).$$
The minus sign is what gives us the anti-commutativity: $$(p \wedge p)(a \times b):=q (a) p(b) - q (b) p(a)=-(p (a) q(b) - p (b) q(a)).$$
Proposition. $$dx \wedge dx=0,\ dy \wedge dy=0.$$
Exercise. Prove the proposition.
Here is an illustration of the relation between the product of cubical chains and the wedge product of cubical cochains:
The general definition is as follows.
Recall that, for our cubical grid ${\mathbb R}^n$, the cells are the cubes given as products: $$Q=\displaystyle\prod _{k=1}^nA _k,$$ with each $A_k$ either a vertex or an edge in the $k$th component of the space. We can derive the formula for the wedge product in terms of these components. If we omit the vertices, a $(p+q)$-cube can be rewritten as $$Q=\displaystyle\prod _{i=1}^{p}I _i \times \displaystyle\prod _{i=p+1}^{p+q}I _i,$$ where $I_i$ is its $i$th edge. The two summands are a $p$-cube and a $q$-cube respectively and can be the inputs of a $p$-cochain and a $q$-cochain respectively.
Definition. The wedge product of the a $p$-cochain and a $q$-cochain is a $(p+q)$-cochain given by its value on the $(p+q)$-cube, as follows: $$\big( \varphi ^p \wedge \psi ^q \big)(Q):= \displaystyle\sum _s (-1)^{\pi (s)}\varphi ^p\Big(\displaystyle\prod _{i=1}^{p}I _{s(i)}\Big) \cdot \psi ^q\Big(\displaystyle\prod _{i=p+1}^{p+q}I _{s(i)}\Big),$$ with summation over all permutations $s\in {\mathcal S}_{p+q}$ with $\pi (s)$ the parity of $s$ (the superscripts are the degrees of the cochains).
Exercise. Verify that $Pdx=P\wedge dx$. Hint: what is the dimension of the space?
Proposition. The wedge product satisfies the skew-commutativity: $$\varphi ^m \wedge \psi ^n= (-1)^{mn} \psi ^n \wedge \varphi ^m.$$
Under this formula, we have the anti-commutativity when $m=n=1$, as above.
Exercise. Prove the proposition.
Unfortunately, the wedge product isn't associative!
Exercise. (a) Give an example of this: $$\phi ^1 \wedge (\psi ^1 \wedge \theta ^1) \ne (\phi ^1 \wedge \psi ^1) \wedge \theta ^1 .$$ (b) For what class of cochain is the wedge product associative?
The crucial difference between the linear operations and the wedge product is that the former two act within the space of $k$-cochains: $$+,\cdot : C^k \times C^k \to C^k;$$ while the latter acts outside: $$\wedge : C^k \times C^m \to C^{k+m}.$$ We can make both operate within the same space if we define them on the graded space of all cochains: $$C^*:=C^0 \oplus C^1 \oplus...$$
The exterior derivative of a $1$- and $1$-cochains in dimension $2$
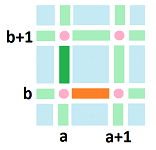
Next we consider the case of the space of dimension $2$ and cochains of degree $1$. Given a $0$-cochain $f$ (in red), we compute its exterior derivative $df$ (in green):
Once again, it is computed by taking differences.
Let's make this computation more specific. We consider the differences horizontally (orange) and vertically (green):
According to our definition, we have:
- (orange) $df\Big([a,a+1] \times \{b\}\Big) := f\Big(\{(a+1,b)\}\Big) - f\Big(\{(a,b)\}\Big)$
- (green) $df\Big(\{a \} \times [b,b+1] \Big) := f\Big(\{(a, b+1)\}\Big) - f\Big(\{(a,b)\}\Big)$. $\\$
Therefore, we have: $$df = \langle \operatorname{grad} f , dA \rangle,$$ where $$dA := (dx,dy), \quad \operatorname{grad} f := (d_xf,d_yf).$$ The notation is justified if we interpret the above as “partial exterior derivatives”:
- $d_xf \Big([a,a+1] \times \{b\}\Big) := f(a+1,b) - f(a,b),$
- $d_yf \Big(\{a \} \times [b,b+1] \Big) := f(a, b+1) - f(a,b)$.
What about the higher degree cochains?
Let's start with $1$-cochains in ${\mathbb R}^2$. The exterior derivative is meant to represent the change of the values of the cochain as we move around the space. This time, we have possible changes as we move in both horizontal and vertical directions. Then we will be able to express these quantities by a single number as a combination of the changes:
If we concentrate on a single square, these differences are computed on the opposite edges of the square.
Just as in the last subsection, the question arises: where to assign this value? Conveniently, the resulting value can be given to the square itself.
We will justify the negative sign in the cochainula below.
With each $2$-cell given a number in this fashion, the exterior derivative of a $1$-cochain is a $2$-cochain.
Exercise. Define and compute the exterior derivative of $1$-cochains in ${\mathbb R}$.
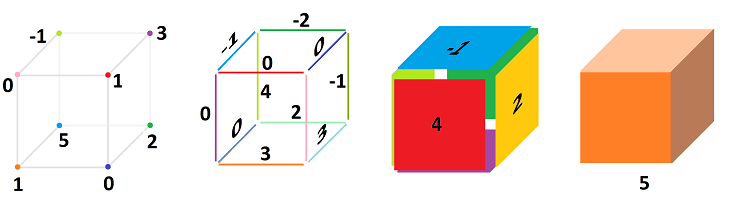
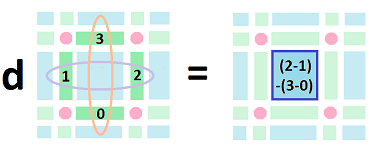
Let's consider the exterior derivative for a $1$-cochain defined on the edges of this square oriented along the $x$- and $y$-axes:
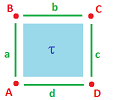
Definition. The exterior derivative $d\varphi$ of a $1$-cochain $\varphi$ is defined by its value at each $2$-cell $\tau$ as the difference of the changes of $\varphi$ with respect to $x$ and $y$ along the edges of $\tau$; i.e., $$d \varphi(\tau) = \Big(\varphi(c) - \varphi(a) \Big) - \Big( \varphi(b) - \varphi(d) \Big).$$
Why minus? Let's rearrange the terms: $$d \varphi(\tau) = \varphi(d) + \varphi(c) - \varphi(b) - \varphi(a).$$ What we see is that we go full circle around $\tau$, counterclockwise with the correct orientations. Of course, we recognize this as a line integral. We can read this formula as follows: $$\displaystyle\int_{\tau}d \varphi=\displaystyle\int _{\partial \tau} \varphi.$$ Algebraically, it is simple: $$d \varphi(\tau) = \varphi(d) + \varphi(c) + \varphi(-b) + \varphi(-a)= \varphi(d+c-b -a) = \varphi(\partial\tau). $$
Thus, the resulting interaction of the operators of exterior derivative and boundary takes the same cochain as for dimension $1$ discussed above: $$d\varphi =\varphi\partial.$$ Once again, it is an instance of the Stokes Theorem, which is used as the definition of $d$.
Let's represent our $1$-cochain as $$\varphi = A dx + B dy,$$ where $A,B$ are the coefficient functions of $\varphi$:
- $A$ is the numbers assigned to the horizontal edges: $\varphi (b),\varphi (d)$, and
- $B$ is the numbers assigned to the vertical edges: $\varphi (a),\varphi (c)$. $\\$
Now, if we think one axis at a time, we use the last subsection and conclude that
- $A$ is a $0$-cochain with respect to $y$ and $dA=\big(\varphi(b) - \varphi(d) \big)dy$, and
- $B$ is a $0$-cochain with respect to $x$ and $dB=\big(\varphi(c) - \varphi(a) \big)dx$. $\\$
Now, from the definition we have: $$\begin{array}{llllllll} d \varphi &= \Big(\big(\varphi(c) - \varphi(a) \big) - \big( \varphi(b) - \varphi(d) \big)\Big)dxdy\\ &= \big(\varphi(c) - \varphi(a) \big)dxdy - \big( \varphi(b) - \varphi(d) \big)dxdy\\ &= \big(\varphi(c) - \varphi(a) \big)dxdy + \big( \varphi(b) - \varphi(d) \big)dydx\\ &= \Big( \big(\varphi(c) - \varphi(a) \big)dx\Big)dy + \Big(\big( \varphi(b) - \varphi(d) \big)dy\Big)dx\\ &= dBdy+dA dx. \end{array}$$
We have proven the following.
Theorem. $$d (A dx + B dy) = dA \wedge dx + dB \wedge dy.$$
Exercise. Show how the result matches Green's Theorem.
In these two subsections, we see the same pattern: if $\varphi \in C^k$ then $d \varphi \in C^{k+1}$ and
- $d \varphi$ is obtained from $\varphi$ by applying $d$ to each of the coefficient functions involved in $\varphi$.
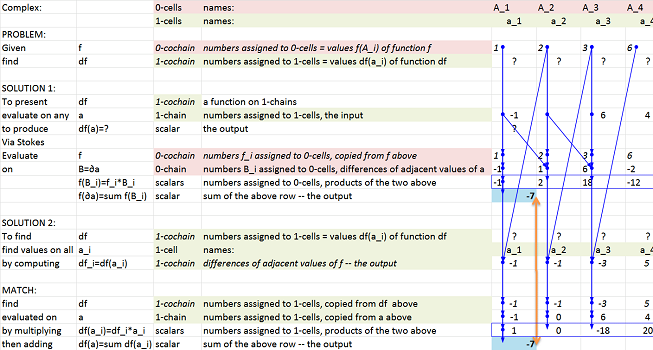
Representing cubical cochains with a spreadsheet
This is how $0$-, $1$-, and $2$-cochains are presented in a spreadsheet:
The difference of $k$-cochains from $k$-chains is only that this time there are no blank $k$-cells!
The exterior derivative in dimensions $1$ and $2$ can be easily computed according to the formulas provided above. The only difference from the algebra we have seen is that here we have to present the results in terms of the coordinates with respect to the cells. They are listed at the top and on the left.
The case of ${\mathbb R}$ is explained below. The computation is shown on the right and explained on the left:
The Excel formulas are hidden but only these two need to be explained:
- first, “$B=\partial a$, $0$-chain numbers $B\underline{\hspace{.2cm}}i$ assigned to $0$-cells, differences of adjacent values of a” is computed by
$$\texttt{ = R[-4]C - R[-4]C[-1]}$$
- second, “$df\underline{\hspace{.2cm}}i=df(a\underline{\hspace{.2cm}}i)$, $1$-cochain, differences of adjacent values of $f$ -- the output” is computed by
$$\texttt{ = R[-16]C - R[-16]C[1]}$$
Thus, the exterior derivative is computed in two ways. We can see how the results match.
Link to file: Spreadsheets.
Exercise. Create a spreadsheet for “antidifferentiation”.
Exercise. (a) Create a spreadsheet that computes the exterior derivative of $1$-cochains in ${\mathbb R}^2$ directly. (b) Combine it with the spreadsheet for the boundary operator to confirm the Stokes Theorem.
A bird's-eye view of calculus
We have now access to a bird's-eye view of the topological part of discrete calculus, as follows.
Suppose we are given the cubical grid ${\mathbb R}^n$ of ${\bf R}^n$. On this complex, we have the vector spaces of $k$-chains $C_k$. Combined with the boundary operator $\partial$, they form the chain complex $\{C_*,\partial\}$ of $K$: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{rrrrrrrrrrrrr} 0& \ra{\partial_{n+1}=0} & C_n & \ra{\partial_n}& ... &\ra{\partial_1} & C_0 &\ra{\partial_0=0} & 0 . \end{array} $$ The next layer is the cochain complex $\{C^*,d\}$, formed by the vector spaces of cochains $C^k=(C_k)^*,\ k=0,1, ...$: $$\newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{rrrrrrrrrrrrr} 0& \la{d_n=0} & C^n & \la{d_{n-1}} & ... & \la{d_0} & C^0 &\la{d_{-1}=0} &0 . \end{array} $$ Here $d$ is the exterior derivative. The latter diagram is the “dualization” of the former as explained above: $$d\varphi (x)=\varphi\partial (x).$$ The shortest version of this formula is as follows.
Theorem (Stokes Theorem). The exterior derivative is the dual of the boundary operator: $$\begin{array}{|c|} \hline \\ \quad \partial ^*=d \quad \\ \\ \hline \end{array}$$
Rather than using it as a theorem, we have used it as a formula that defines the exterior derivative.
The main properties of the exterior derivative follow.
Theorem. The operator $d: C^k \to C^{k+1}$ is linear.
Theorem (Product Rule - Leibniz Rule) $$d(\varphi \wedge \psi) = d \varphi \wedge \psi + (-1)^k \varphi \wedge d \psi .$$
Exercise. Prove the theorem for dimension $2$.
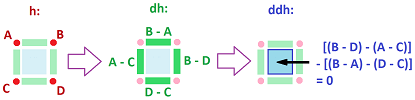
Theorem (Double Derivative Identity). $dd : C^k \to C^{k+2}$ is zero.
Proof. We prove only $dd=0 : C^0({\mathbb R}^2) \to C^2({\mathbb R}^2)$.
Suppose $A,B,C,D$ are the values of a $0$-cochain $h$ at these vertices:
We compute the values of $dh$ on these edges, as differences. We have: $$-(B-A) + (C-D) + (B-C) - (A-D) = 0,$$ where the first two are vertical and the second two are horizontal. $\blacksquare$
In general, the property follows from the double boundary identity.
The proof indicates that the two mixed partial derivatives are equal: $$\Phi_{xy} = \Phi_{yx},$$ just as in Clairaut's Theorem.
Exercise. Prove $dd : C^1({\mathbb R}^3) \to C^3({\mathbb R}^3)$ is zero.
Exercise. Compute $dd : C^1 \to C^3$ for the following cochain: