This site is being phased out.
Continuity of functions of several variables
Before we consider continuity of functions of several variables, let's recall how the issue is handled in Calc1 as there is a subtle difference.
Problem. For the function $$f(x) = \sqrt{x}$$
discuss continuity.
- at $x = 0$, $f$ is not continuous. However it is right-continuous at $\{0 \}$ as $x = 0$ is the end point of $D(f)$.
- at $x > 0$, $f$ is continuous.
- for $x < 0$, f is undefined.
Thus $f$ is continuous on on $( 0, \infty )$ or continuous in the extended sense on $[ 0, \infty )$.
Recall the definition. A function $$f \colon {\bf R} \rightarrow {\bf R}$$
is continuous at point $a \in {\bf R}$ if for any $\epsilon > 0$ there is a $\delta > 0$ such that $| x - a | < \delta \rightarrow |f(x)-f(a)| < \epsilon$.
Note that the definition implicitly assumes that $x, a \in$ $D(f)$.
How does the definition change in the $n$-dimensional case?
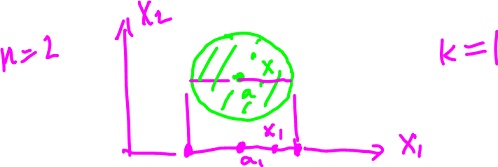
Definition. A function $$f \colon {\bf R}^n \rightarrow {\bf R}, f(\vec{x}) = y,$$ is continuous at point $\vec{a} \in D(f)$ if for any $\epsilon > 0$ there is a $\delta > 0$ such that $|| \vec{x} - \vec{a} || < \delta$ and $\vec{x} \in D(f) \rightarrow || f(\vec{x}) - f(\vec{a}) || < \epsilon$.
First, we have replaced the absolute value with the norm and unidimensional $x$ with multidimensional $\vec{x}$. This simply reflect the way we measure "closeness" in ${\bf R}$ versus in ${\bf R}^n$ (see Continuous functions).
Second, $x$ is required to be in the domain of $f$. This makes a difference. With the new definition, $\sqrt{x}$ is continuous on $[ 0, \infty )$ (verify). Thus one-side continuity is no longer an issue.
Now for ${\rm dim} > 1$.
Example. Consider $$f( x, y ) = ( x + y )^{\frac{1}{2}},$$ $$D(f) = { ( x, y ): x + y ≥ 0 }.$$
Without actually verifying the definition, we see that the function is continuous on the whole domain - the half-plane including the border.
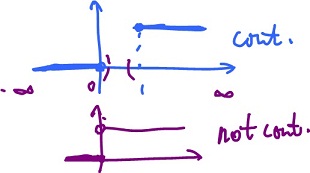
Example. Let $$f(x) = \left\{ \begin{array}{ll} 0 &: x \leq 0 \\ 1 &: x \geq 0 \end{array} \right. .$$
Is $f$ continuous? Yes! It is surprising, but since the domain is "disconnected", the function can't be (unlike the second example on the right).
Example. Let $$f(x) = c$$ a constant function. Then $$|| f(x) - f(a) || = || c - c || = 0 < \epsilon,$$
so $f$ is continuous.
Theorem. Let $$f \colon {\bf R}^n \rightarrow {\bf R}$$ $$f_k(x) = x_k,$$ be the projection, where $$x = ( x_1, \ldots , x_n ).$$
Then $f$ is continuous.
(For example, if $n = 3$, $f_2( 1, 5, 7 ) = 5$.)
Proof. Consider $$f_k(x) = a_k,$$ where $a = ( a_1, ..., a_n )$.
In order to show this, we have to find $\delta$ for a given $\epsilon > 0$. We hence want to show that for $$|| x - a || < \delta$$ it follows that $$| f_k(x) - f_k(a) | = | x_k - a_k | < \epsilon.$$
We rewrite $$((x_1 - a_1)^2 + (x_2-a_2)^2 + \ldots)^{\frac{1}{2}} < \delta,$$ and $$((x_1-a_1)^2+(x_2-a_2)^2+ \ldots)^{\frac{1}{2}} \geq ((x_k-a_k)^2)^{\frac{1}{2}} = |x_k-a_k| < \epsilon$$
Choose $\delta = \epsilon$. Then if $$((x_1-a_2)^2+(x_2-a_2)^2+ \ldots)^{\frac{1}{2}} < \delta = \epsilon$$ then $$| x_k - a_k | < \epsilon.$$
A more topological discussion follows.
The continuity of function $f$ of one variable at point $x=a$ can be defined in terms of closeness (proximity):
This is the usual definition of continuity of a real valued function of single variable $f$ at point $x=a$:
The second part can be easily rewritten for a function several variables with the norm replacing the absolute value:
Definition 1. Given a function $f \colon {\bf R}^n \rightarrow {\bf R}^m$, it is continuous at $x=a$ if
This definition still follows the proximity idea above.
However, this is not the way the continuity of a function of $n$ variables is defined.
Definition 2. A function $f \colon {\bf R}^n \rightarrow {\bf R}^m$ is represented as a combination of $m$ functions of $n$ variables: $$f(x) = (f_1(x), f_2(x), \ldots , f_m(x)), {\rm \hspace{3pt} where \hspace{3pt}} x = (x_1, x_2, \ldots , x_n).$$
Then $f$ is called continuous if each of the functions $$f_1, f_2, ..., f_m \colon {\bf R}^n → {\bf R}$$ is continuous. Now, a function $g \colon {\bf R}^n \rightarrow {\bf R}$ is called continuous at $x=a$ if it is continuous with respect to each of these variables:
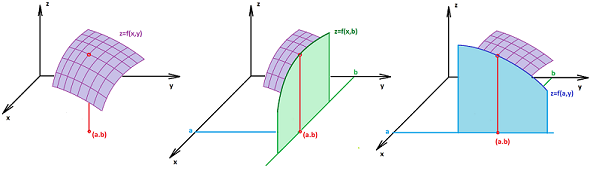
- for each combination $a_1, a_2, \ldots, a_n$ and each $k$, the function $h \colon {\bf R}^n \rightarrow {\bf R}$ given by
$$h(u) = g(a_1, a_2, ..., a_{k-1}, u, a_{k+1}, ..., a_n)$$ is continuous at $u=a_k$ as a function of single variable.
For example, define $f \colon {\bf R}^2 \rightarrow {\bf R}^2$ by $$f(x,y)=({\rm sin}(xy), x+y).$$
It is continuous because for each $a,b$ the functions $${\rm sin}(ay), {\rm sin}(xb), a+y, {\rm \hspace{3pt} and \hspace{3pt}} x+b$$ are continuous functions of $x$ or $y$ respectively.
This means, in particular, that if the graph of ${\rm sin}(xy)$ is cut by a plane parallel to the $xz$-plane or the $yz$-plane, the result is a continuous curve. Meanwhile, Definition $1$ suggests that this graph is a continuous surface. One would expect that the latter implies the former, but, as it turns out, these two definitions are equivalent.
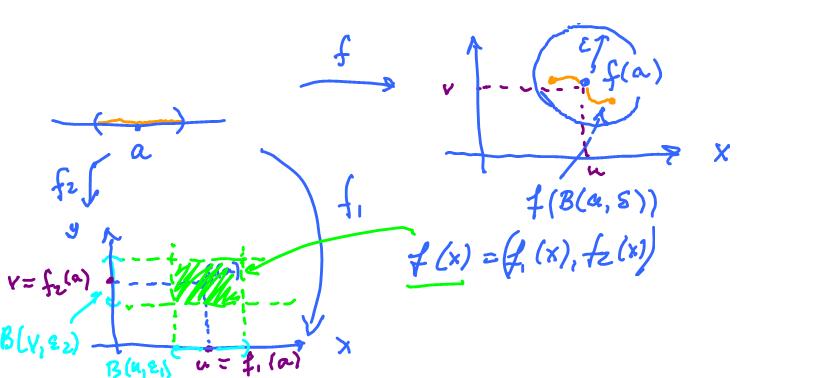
To illustrate let's show that for a function $f \colon {\bf R} \rightarrow {\bf R}^2$ (a parametric curve) Definition $2$ implies Definition $1$. The idea of the proof comes from the purely topological approach to continuity (see Continuous functions). The definition can be re-written one more time with: $${\rm if \hspace{3pt}} x \in B(a,\delta), {\rm \hspace{3pt} then \hspace{3pt}} f(x) \in B(f(a),\epsilon),$$ where $B(p,d)= \{u \colon ||u-p|| < d\}.$
Now we use the observation that no matter how small a circle is, one can always inscribe a square inside: $${\rm if \hspace{3pt}} q < \frac{\epsilon}{\sqrt{2}}, {\rm \hspace{3pt} then \hspace{3pt}} \{(x,y) \colon |x-a| < q, |y-b| < q \} \subset B((a,b), \epsilon) = \{(x,y) \colon ||(x,y)-(a,b)|| < \epsilon \}.$$
Also, for the converse, it suffices to consider the opposite situation. Expressed in other words, these two collections form two bases of the same topology on ${\bf R}^2$, see Introduction to point-set topology.
Suppose a is a real number. Given $\epsilon >0$, we need to prove that there is $\delta >0$ such that $${\rm if \hspace{3pt}} |x - a| < \delta, {\rm \hspace{3pt} then \hspace{3pt}} || f(x) - f(a) || < \epsilon.$$
Suppose $f = (f_1, f_2)$. For $i=1,2$, since $f_i$ is continuous at $a$, there is $\delta_i$ such that $${\rm if \hspace{3pt}} |x - a| < \delta_i {\rm \hspace{3pt} then \hspace{3pt}} | f_i(x) - f_i(a) | < \epsilon' = \frac{\epsilon}{\sqrt{2}}.$$
Let $$\delta = {\rm min}\{ \delta_1, \delta_2 \}.$$ Then $${\rm if \hspace{3pt}} |x - a| < \delta {\rm then \hspace{3pt}} | f_i(x) - f_i(a) | < \epsilon' = \frac{\epsilon}{\sqrt{2}}.$$
As explained above, we need these inequalities to conclude that $$(f_1(x) - f_1(a))^2 + (f_2(x) - f_2(a))^2 < \epsilon^2.$$ The right-hand side is the square of the norm, hence $${\rm if \hspace{3pt}} |x - a| < \delta {\rm \hspace{3pt} then \hspace{3pt}} || f(x) - f(a) || < \epsilon.$$ $\blacksquare$