Computing homology

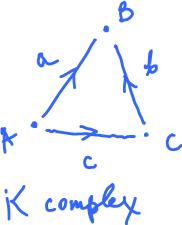
Homology in dimension 1

Recall that given a cell complex $K$, a $k$-chain is a "formal" linear combination of finitely many oriented $k$-cells, such as $3a + 5b - 17c$ with, typically, integer coefficients. Then the set of all $k$-chains $C_k(K)$ is an abelian group with respect to chain addition generated by the $k$-cells of $K$: $$C_k(K) = \left\{ \displaystyle\sum_i s_i \sigma_i \colon s_i \in {\bf Z}, \sigma_i {\rm \hspace{3pt} is \hspace{3pt} a \hspace{3pt}} k{\rm -cell \hspace{3pt} in \hspace{3pt}} K \right\}.$$

Now a relation will be established between cells/chains of different dimensions in order to capture the topology of the cell complex. This relation is given by the boundary operator.

The boundary of a vertex empty, so the boundary operator of a $0$-chain is $0$: $$\partial (A) = 0 {\rm \hspace{3pt} for \hspace{3pt} any \hspace{3pt}} A \in C_0(K).$$

The boundary of a $1$-cell consists of its two end-points, so in the binary setting this was simple: $$\partial (a) = \partial (AB) = A + B.$$

In the integral setting, the direction of the edge matters ($AB \neq BA$), so we define: $$\partial (a) = \partial (AB) = B - A {\rm \hspace{3pt} for \hspace{3pt} any \hspace{3pt}} a = AB \in C_1(K).$$ On the other hand, $$\partial (BA) = A - B,$$ which makes sense since $BA = -AB$.

Let's define the boundary operator. First,

the boundary of a oriented (directed) $1$-cells is the $0$-chain: endpoint - initial point.

Or $$\partial (AB) = B - A$$

Now extend this definition to the whole chain complex, by assuming that $\partial$ is a homomorphism (or a linear operator in the vector space case):

if $a = \displaystyle\sum_i s_i \sigma_i, s_i \in {\bf Z}, $ then $\partial(a) = \displaystyle\sum_i s_i \partial(\sigma_i)$.

In other words we define the boundary operator on the generators (cells) of the group and then extend it to the whole group by linearity.

In the above example, the boundary operator evaluated on the generators: $$\partial (a) = \partial (AB) = B - A,$$ $$\partial (b) = \partial (CB) = B - C,$$ $$\partial (c) = \partial (AC) = C - A;$$

on other chains: $$\partial (a + b) = \partial (a) + \partial (b) = B - A + B - C = 2B - A - C,$$ $$\partial (a + b + c) = \partial (a) + \partial (b) + \partial (c) = B - A + B - C + C - A = 2B - 2A.$$

It may appear that in the above picture, that $a, b$, and $c$ form a circle. They do unless take into account their directions. To confirm this algebraically we need to see what's the boundary of the chain $a + b + c$: $$\partial (a + b + c) = B - A + B - C + C - A = -2A + 2B.$$

This isn't zero so $a + b + c$ isn't a cycle.

Which chain is? It's $a - b - c$: $$\partial (a - b - c) = 0.$$

But so is $2a - 2b - 2c, 3a - 3b - 3c$, and all other of its multiples. So, the cycles is a subgroup generated by $a - b - c$: $$Z_1(K) = <a - b - c>.$$

Definition. A chain is called a cycle if its boundary is $0$.

Theorem. The cycles form a subgroup $Z_k(K)$ of the chain group $C_k(K)$ which is the kernel of the boundary operator: $$Z_k(K) = {\rm ker}( \partial ).$$

This subgroup is called the cycle group.

In the above example, we have: $$Z_1(K) = <a - b - c> = {\bf Z} < C_1(K) = {\bf Z}^3.$$

We showed that all of these chains are cycles, but how do we know that we've found all of them? Let's solve the problem properly.

Topology problem. Evaluate $Z_1(K)$ for $K$ given above.

For simplicity we assume that these are real chains: $$\displaystyle\sum_i s_i \sigma_i, s_i \in {\bf R}.$$

Then this is what we know: $$\partial \colon C_1(K) \rightarrow C_0(K) = {\bf R}^3$$ is a linear operator between two copies of ${\bf R}^3$ with bases $\{a, b, c \}$ and $\{A, B, C \}$ respectively. The values of $\partial$ on the basis elements are given above. Now to solve our problem, we observe that: $$x \in C_1(K) {\rm \hspace{3pt} is \hspace{3pt} a \hspace{3pt} cycle \hspace{3pt} iff \hspace{3pt}} \partial x=0.$$ But $x$ can be expressed as a linear combination of the elements of the basis: $$x = ua + vb + wc.$$ Then the condition above can be rewritten as new $$\partial (ua + vb + wc) = 0,$$ or $$\partial (ua) + \partial (vb) + \partial (wc) = 0$$ or $$u(B - A) + v(B - C) + w(C - A) = 0.$$ After collecting similar terms, we can restate or problem.

Linear algebra problem. Find real numbers (turns out integers) $u, v$, and $w$ such that $$(-u-w)A + (u+v)B + (-v+w)C = 0.$$

Since $\{A, B, C \}$ is a basis, these elements are linearly independent. Hence each of their coefficients is $0$: $$-u - w = 0,$$ $$u + v = 0,$$ $$-v + w = 0.$$

This is a (homogeneous) system of linear equations. It can be solved in a number of ways. For example, take $w = v$ from the last equation and substitute it into the first, then we have $$-u - v = 0,$$ $$u + v = 0.$$ Substitute again and we have $u = -v$. Then, the solutions are $$u = -t, v = t, w = t {\rm \hspace{3pt} for \hspace{3pt}} t \in {\bf R}.$$ Or, the solution set is span$\{(-1, 1, 1) \}$.

Now, back to topology: $$Z_1(K) = {\rm span}\{(-a+b+c)\}.$$ Since there are no $2$-cells, no two $1$-chains are homologous. So $$H_1(K) = Z_1(K) = {\rm span}\{(-a + b + c) \},$$ or, in the group case, $$H_1(K) = <(-a + b + c)>.$$

Adding however a face to this triangle will make $-a + b + c$ homologous to $0$. See Homology in dimension 2.

Exercise. Compute the homology (by solving a system of linear equations) of the figure eight, represented by a cell complex with (a) $5$ edges, (b) $2$ edges.

For a more concrete way of capturing $0$- and $1$-cycles, see Homology of images.

Homology in dimension 2

Definition. The $k$-boundary group of cell complex $K$ is the set of all boundaries of the $(k+1)$-chains in $K$, i.e., it's the image of the $(k+1)$-chain group: $$B_k(K) = \partial (C_{k+1}(K)).$$

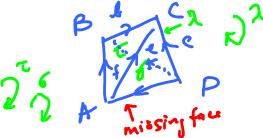
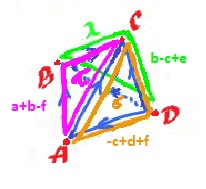
Let's consider another example. Suppose $K$ is a $3$-face pyramid (no bottom face):

• $\dim 0: A, B, C, D;$
• $\dim 1: a, b, c, d, e, f$;
• $\dim 2: \lambda, \sigma, \tau$.

Topology problem. Find all $1$-cycles that are boundaries of $2$-chains.

In other words, we need to compute the boundary group $B_1(K)$. This is what we know: $$\partial \lambda = a + b - f,$$ $$\partial \sigma = f - c + d,$$ $$\partial \tau = -c + e + b.$$

In the vector space environment, $$C_2(K) = {\bf R}^3, C_1(K) = {\bf R}^6,$$ so the boundary operator $$\partial \colon C_2(K) \rightarrow C_1(K)$$ is represented by a $6 \times 3$ matrix.

Exercise. (a) Without finding the matrix, what are the possible outcomes for the image of $\partial$? (b) Find the matrix of $\partial$.

Linear algebra problem. Find the image of the linear operator $\partial$.

We need to find all $u = \partial ( \alpha ), \alpha \in C_2(L)$. Suppose $$u = x\lambda + y\sigma + z\tau, {\rm \hspace{3pt} for \hspace{3pt} some \hspace{3pt}} x, y, z \in {\bf R}.$$

Then $$\begin{array}{l} \partial u &= x \partial \lambda + y \partial \sigma + z \partial \tau \\ &= x(a + b - f) + y(f - c + d) + z(-c + e + b) \\ &= xa + (x + z)b + (-y - z)c + yd + ze + (-x + y)f \end{array}$$

Or, $$\partial \colon [x,y,z] \rightarrow [x, x + z, -y - z, y, z, -x + y].$$

Is there a $1$-chain ($6$-vector) that's not here?

Let's try $a = [1, 0, 0, 0, 0, 0]$. Is this a boundary?

Compute: $$x = 1 \rightarrow z = -1, y = 1,$$ so, no!

What about $t = [1, 0, 0, 1, -1, 0]$? At the first sight it may seem that since $t$ is the boundary of the missing face, it's not a boundary in $K$. We can see why this is wrong by looking at the image on the right or, even better, we can just let algebra do the work.

From the equations, $$\begin{array}{} x = 1, \\ x + z = 0 \rightarrow z = -1, \\ -y - z = 0 \rightarrow y = 1, \\ y = 1, \\ z = -1, \\ -x + y = 0. \end{array}$$

So, $$t = \partial [1, 1, -1].$$

This is what we have to deal with: $$\begin{array}{} x_1 = x, \\ x_2 = x + z, \\ x_3 = -y - z, \\ x_4 = y, \\ x_5 = z, \\ x_6 = -x + y. \end{array}$$

To capture all possible vectors $[x_1, ..., x_6]$ we can treat $x, y$, and $z$ as parameters. Since $$\partial ([x,y,z]) = \partial (xa + yb + zc),$$ the image of $\partial$ is spanned by $$p = \partial (a) = [1, 1, 0, 0, 0, -1]$$ $$q = \partial (b) = [0, 0, -1, 1, 0, 1], $$ $$r = \partial (c) = [0, 1, -1, 0, 1, 0].$$

Next, by solving a homogeneous system of linear equations, we show that $p, q, r$, are linearly independent. Therefore, $\{p, q, r \}$ is a basis of $B_1(K)$.

A topological interpretation of this result is simple:

Exercise. Represent the torus as a cell complex with two $2$-cells, compute the boundary group $B_1(K)$ by solving a system of linear equations (as above).

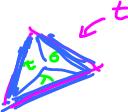
Example. Compute the homology of sphere with membrane.

Cells of $K$:

• $2$-cells: $\mu, \sigma, \tau$,
• $1$-cells: $e$,
• $0$-cells: $A$.

Chain groups:

• $C_2(K) = {\rm span}\{\mu, \sigma, \tau \} = {\bf R}^3,$
• $C_1(K) = {\rm span}\{e \} = {\bf R},$
• $C_0(K) = {\rm span}\{A \} = {\bf R}.$

The boundary operator: $$\partial \colon 0 \rightarrow {\bf R}^3 \rightarrow {\bf R} \rightarrow {\bf R} \rightarrow 0.$$

• $\dim 0$:

$$Z_0(K) = C_0(K).$$

Always, since $\partial \colon {\bf R} \rightarrow 0$, its kernel is the whole domain. So $$Z_0(K) = {\rm span}\{A \}.$$

Next, $$\partial e = A - A = 0,$$ so $$B_0(K) = {\rm span}\{∂e \} = 0,$$ so $$H_0(K) = Z_0(K) / B_0(K) = {\rm span}\{A \} / 0 = {\rm span}\{A \}.$$

So, there is only one piece here.

• $\dim 1$:

Since $\partial e = 0$, the boundary operator $$\partial \colon C_1(K) = {\rm span}\{e \} \rightarrow C_0(K) = {\rm span}\{A \}$$ is zero.

Hence, $$Z_1(K) = {\rm ker \hspace{3pt}} \partial = {\rm span}\{e \}.$$

Observe: $$\begin{array}{l} \partial \mu = -e, \\ \partial \sigma = e, \\ \partial \tau = e. \end{array}$$

Then $$B_1(K) = {\rm span}\{ \partial \mu, \partial \sigma, \partial \tau \} = {\rm span}\{e \},$$ and $$H_1(K) = Z_1(K) / B_1(K) = {\rm span}\{e \} / {\rm span}\{e \} = 0.$$

So, there are no non-trivial loops here.

• $\dim 2$:

Since the dimension of the image of the boundary operator $$\partial \colon C_2(K) = {\rm span}\{ \partial \mu, \partial \sigma, \partial \tau \} \rightarrow C_1(K) = {\rm span}\{e \}$$ is $1$, then the dimension of its kernel is $3 - 1 = 2$.

Let's find its basis by solving the system of linear equations $\partial x = 0$. By examination: $$\partial (\mu + \tau) = e - e = 0,$$ $$\partial (\mu + \sigma) = e - e = 0,$$ so $\{\mu + \tau, \mu + \sigma \}$ is a basis of $Z_2(K)$. Finally, $$H_2(K) = Z_2(K) / B_2(K) = {\rm span}\{\mu + \tau,\mu + \sigma \} / 0 = {\rm span}\{ \mu + \tau,\mu + \sigma \}.$$

These two elements represent the two voids in the sphere. (Note: $\mu - \tau, \sigma + \mu$, etc may also form a basis.)

Exercise. Compute the homology of the sphere with a string from $N$ to $S$.

Examples of homology of cubical complexes

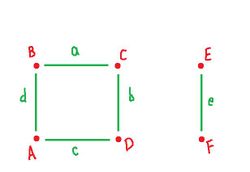
Let's construct a cubical complex for the disjoint union of a circle and an line segment and compute its homology, $X$.

The simplest way to capture the topology of $X$ is by considering a square and an edge as on the right. Its cubical representation includes $5$ edges and $5$ vertices. We name them as shown.

More specifically below we present the cubical complex $K$ of $X$:

• Part $1$, list of all cells:
  • $0$-cells: $\{A, B, C, D, E, F \}$
  • $1$-cells: $\{a, b, c, d, e \}$
• Part 2, list of the boundaries of all cells:
  • $0$-cells: ${\partial}A = 0, {\partial}B = 0, {\partial}C = 0, {\partial}D = 0, {\partial}E = 0, {\partial}F = 0$
  • $1$-cells: ${\partial}a = B + C, {\partial}b = C + D, {\partial}c = D + A, {\partial}d = A + B, {\partial}e = E + F$

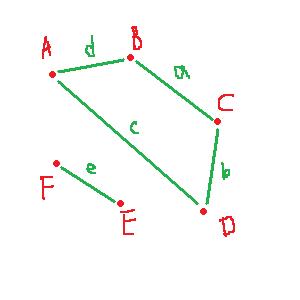
As an exercise let's reconstruct $X = |K|$ from $K$. First we randomly throw the $0$-cells (Part 1) on the plane:

(This is called the $0$-skeleton of $K$.)

Then we add the $1$-cells (Part 1) according to their boundaries (Part 2):

This is the $1$-skeleton of $K$.

The outcome is different from $X$ but homeomorphic to it. Note that if the order of $0$-cells was different, we'd have to put them in 3D space to avoid intersections of cells. This is possible for any complex if we choose the ambient space of high enough dimension.

Next we compute the homology. First dimension $0$. From the boundaries of $1$-cells (Part 2) we know:

$$B \sim C, C \sim D, D \sim A, A \sim B, E \sim F.$$

Therefore we have two equivalence classes:

$[A] = \{A, B, C, D \}$ and $[E] = \{E, F \}$,

as well as their sum. So, the homology group $H_0(K)$ of $K$ is generated by these two classes:

$$H_0(K) = <[A], [E]>.$$

Now dimension $1$. From examination of the boundaries of $1$-cells, ones sees that the only non-zero $1$-cycle is $q = a + b + c + d$. Now, since there are no $2$-cells, this cycle isn't homologous to $0$. So,

$$H_1(K) = <[q]>.$$

Thus the Betti numbers are $2$ and $1$.

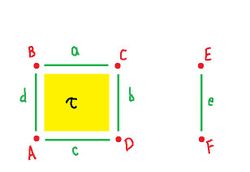
Further, what happens if there is a $2$-cell $\tau$ on the left?

This is the new complex:

• Part $1$, list of all cells:
  • $0$-cells: $\{A, B, C, D, E, F \}$
  • $1$-cells: $\{a, b, c, d, e \}$
  • $2$-cells: $\{ \tau \}$
• Part 2, list of the boundaries of all cells:
  • $0$-cells: ${\partial}A = 0, {\partial}B = 0, {\partial}C = 0, {\partial}D = 0, {\partial}E = 0, {\partial}F = 0 $
  • $1$-cells: ${\partial}a = B + C, {\partial}b = C + D, {\partial}c = D + A, {\partial}d = A + B, {\partial}e = E + F$
  • $2$-cells: ${\partial} \tau = a + b + c + d = q$

Then there are no changes in dimension $0$:

$$H_0(K) = <[A], [E]>.$$

And in dimension $1$ the only non-zero cycles, $q$, is now homologous to $0$, so $$H_1(K) = 0.$$

This is a cube (empty), i.e., a topological sphere.

The list of cell is already given. To present the cubical complex, write the boundaries.

Exercise. Compute its homology.

How to compute Betti numbers

One can acquire the Betti numbers from the homology groups (and cohomology) by taking their dimensions/ranks. However, sometimes we need only to count the topological features. The we should compute the Betti numbers directly.

In this article, we re-write How to compute homology with simplification that this approach allows us.

We summarize the procedure for computing the Betti numbers of a cell complex, by hand.

Step 1: present the cell complex

List the cells of the complex $K$. Try to find the most economical representation - start with the highest dimension. Then merge the cells whenever possible and use cell collapse as well. Indicate the orientations. List the boundaries of the cells.

Step 2: find the chain groups

The $k$-chain group $C_k(K)$ is given as a vector space with basis consisting of the cells of the complex:

$C_k(K) =$ span$\{k$-cells in $K\}$.

Its dimension is then obvious.

Step 3: find the matrices of the boundary operators

The $k$-boundary operator

$${\partial}_k: C_k(K) {\rightarrow} C_{k-1}(K)$$

is a linear operator. As such it is determined by its values on the elements of the basis of the domains space $C_k(K)$, the $k$-cells, as they are expressed as linear combinations of the elements of the basis of the target space $C_{k-1}(K)$, the $(k-1)$-cells. The coefficients of these linear combinations form the columns of the matrix.

Step 4: find the dimensions of the cycle groups

The $k$-cycle group is the kernel of the $k$-boundary operator:

$$Z_k(K) = \ker {\partial}_k.$$

As such it is the solution of the matrix equation:

find all $x \in C_k(K)$ such that ${\partial}_k(x) = 0$.

It is a subspace of the chain group $C_k(K)$. One finds it by finding the rank of the matrix of ${\partial}_k$:

$$\dim Z_k(K) = \dim C_k(K) - {\rm \hspace{3pt} rank \hspace{3pt}} {\partial}_k. $$

Shortcuts:

• if ${\partial}_k$ is $0$, its kernel is the whole domain space and:

$$\dim Z_k(K) = \dim C_k(K).$$

• if ${\partial}_k$ is one-to-one, its kernel is $0$:

$$\dim Z_k(K) = 0.$$

Step 5: find the dimensions of the boundary groups

The $k$-boundary group is the image of the $(k+1)$-boundary operator:

$$B_k(K) = {\partial}_{k+1}.$$

As such it is spanned by the images of the basis of the $(k+1)$-cycle group, $(k+1)$-cells:

$B_k(K) = {\rm \hspace{3pt} span}\{ \partial_{k+1}(s_i): s$ is a $(k+1)$-cell in $K \}$.

It is a subspace of the cycle group $Z_k(K)$. One finds it by finding the rank of the matrix:

$$\dim B_k(K) = {\rm \hspace{3pt} rank \hspace{3pt}} {\partial}_{k+1}. $$

Shortcuts:

• if ${\partial}_{k+1}$ is onto, its image is the whole target space and:

$$\dim B_k(K) = \dim C_k(K).$$

• if ${\partial}_{k+1}$ is $0$, its image is $0$:

$$\dim B_k(K) = 0.$$

Step 6: find the Betti numbers

The homology group is the quotient vector space of cycles over boundaries:

$$H_k(K) = Z_k(K) / B_k(K).$$

It is a vector space of dimension

$$b_k(K) = \dim Z_k(K) - \dim B_k(K).$$

Shortcuts: $$\dim Z_k(K) = \dim B_k(K) \rightarrow b_k(K) = 0,$$

$$\dim B_k(K) = 0 \rightarrow b_k(K) = \dim Z_k(K).$$

Example

Step 1: present the cell complex

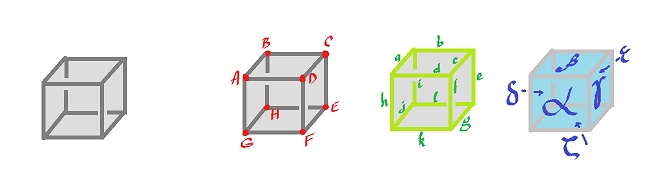
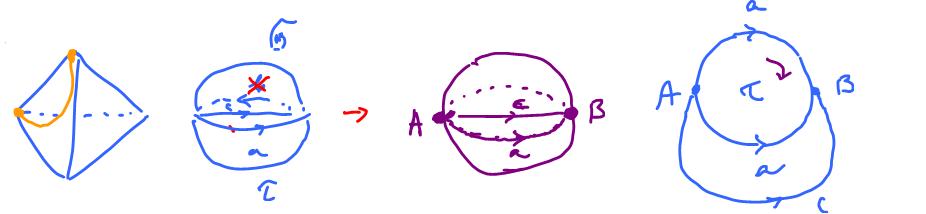
One may choose to triangulate the sphere and then add the string (first image). A more efficient way is to cut the sphere into two hemispheres (second image). Turns out, one can remove one of the edges and merge the hemispheres. One $2$-cells is enough (third image).

Cells and their boundaries: $$\dim 2: {\tau}, {\partial}_2{\tau} = a - a = 0;$$ $$\dim 1: a, c, {\partial}_1a = B - A, {\partial}_1c = B - A;$$ $$\dim 0: A, B, {\partial}_0A = 0, {\partial}_0B = 0.$$

Step 2: find the chain groups

$$C_2(K) = {\rm \hspace{3pt} span \hspace{3pt}} \{\tau \} = {\bf R},$$ $$C_1(K) = {\rm \hspace{3pt} span \hspace{3pt}}\{a, c \} = {\bf R}^2,$$ $$C_0(K) = {\rm \hspace{3pt} span \hspace{3pt}} \{A, B \} = {\bf R}^2.$$

Step 3: find the matrices of the boundary operators

$${\partial}_2: C_2(K) {\rightarrow} C_1(K), {\bf R} {\rightarrow} {\bf R}^2,$$

$${\partial}_2 = [0, 0]^T = \left| \begin{array}{} 0 \\ 0 \end{array} \right| ;$$

$${\partial}_1: C_1(K) {\rightarrow} C_0(K), {\bf R}^2 {\rightarrow} {\bf R}^2,$$

$${\partial}_1 = \left| \begin{array}{rr} -1 & -1 \\ 1 & 1 \end{array} \right| ;$$

$${\partial}_0: C_0(K) {\rightarrow} 0, {\bf R}^2 {\rightarrow} 0,$$

$${\partial}_0 = [0, 0]^T = \left| \begin{array}{} 0 \\ 0 \end{array} \right| .$$

Chain complex:

$$0 {\rightarrow} C_0(K) {\rightarrow} C_0(K) {\rightarrow} C_0(K) {\rightarrow} 0.$$

Step 4: find the dimensions of the cycle groups

$${\partial}_2 = 0 \rightarrow \dim Z_2(K) = 1.$$

$${\partial}_1a = {\partial}_1c = B - A \rightarrow {\rm \hspace{3pt} rank \hspace{3pt}} {\partial}_1 = 1 \rightarrow \dim Z_1(K) = 1.$$

$${\partial}_0 = 0 \rightarrow \dim Z_0(K) = 2.$$

Step 5: find the dimensions of the boundary groups

$$\dim B_2(K) = 0,$$ $$\dim B_1(K) = 0,$$ $$\dim B_0(K) = 1.$$

Step 6: find the Betti numbers

$$b_2(K) = \dim Z_2(K) - \dim B_2(K) = 1;$$ $$b_1(K) = \dim Z_1(K) - \dim B_1(K) = 1;$$ $$b_0(K) = \dim Z_0(K) - \dim B_0(K) = 1.$$

How to compute homology

In this article we summarize the procedure for computing the homology of a cell complex, by hand.

Step 1: present the cell complex

List the cells of the complex $K$. Try to find the most economical representation - start with the highest dimension. Then merge the cells whenever possible and use cell collapse as well. Indicate the orientations. List the boundaries of the cells.

Step 2: find the chain groups

The $k$-chain group $C_k(K)$ is given as a vector space with basis consisting of the cells of the complex:

$C_k(K) =$ span$\{k$-cells in $K \}$.

Its dimension is then obvious.

Step 3: find the matrices of the boundary operators

The $k$-boundary operator

$${\partial}_k: C_k(K) {\rightarrow} C_{k-1}(K)$$

is a linear operator. As such it is determined by its values on the elements of the basis of the domains space $C_k(K)$, the $k$-cells, as they are expressed as linear combinations of the elements of the basis of the target space $C_{k-1}(K)$, the $(k-1)$-cells. The coefficients of these linear combinations form the columns of the matrix.

Step 4: find the cycle groups

The $k$-cycle group is the kernel of the $k$-boundary operator:

$$Z_k(K) = \ker {\partial}_k.$$

As such it is the solution of the matrix equation:

find all $x{\in}C_k(K)$ such that ${\partial}_k(x) = 0$.

It is a subspace of the chain group $C_k(K)$. One finds it by finding its basis.

Shortcuts:

• if ${\partial}_k$ is $0$, its kernel is the whole domain space:

$$Z_k(K) = C_k(K).$$

• if ${\partial}_k$ is one-to-one, its kernel is $0$:

$$Z_k(K) = 0.$$

Otherwise the problem is reduced to solving the homogeneous system of linear equations that corresponds to the matrix equation.

Step 5: find the boundary groups

The $k$-boundary group is the image of the $(k+1)$-boundary operator:

$$B_k(K) = {\partial}_{k+1}.$$

As such it is spanned by the images of the basis of the $(k+1)$-cycle group, $(k+1)$-cells:

$B_k(K) = {\rm \hspace{3pt} span \hspace{3pt}} \{\partial_{k+1}(s_i): s$ is a $(k+1)$-cell in $K \}.$

It is a subspace of the cycle group $Z_k(K)$. One finds it by finding its basis.

Shortcuts:

• if ${\partial}_{k+1}$ is onto, its image is the whole target space:

$$B_k(K) = C_k(K).$$

• if ${\partial}_k$ is $0$, its image is $0$:

$$B_{k+1}(K) = 0.$$

Otherwise the problem is solved by removing vectors from the spanning set to make it linearly independent. The problem is reduced to solving the homogeneous system of linear equations:

find $a_i$ such that $\displaystyle\sum_ia_i{\partial}_{k+1}(s_i) = 0.$

Step 6: find the homology groups

The homology group is the quotient vector space of cycles over boundaries:

$$H_k(K) = Z_k(K) / B_k(K).$$

It is a vector space of dimension

$$\dim H_k(K) = \dim Z_k(K) - \dim B_k(K),$$

which gives us the Betti numbers of $K$. This vector space is the space of equivalence classes on the cycle group:

for $x,y{\in}Z_k(K), x {\sim} y$ if $x - y{\in}B_k(K)$.

Shortcuts:

$$Z_k(K) = B_k(K) \rightarrow H_k(K) = 0,$$ $$B_k(K) = 0 \rightarrow H_k(K) = Z_k(K).$$

Otherwise, one has to remove the elements of the basis of the cycle group that are equivalent to $0$.

Example

Step 1: present the cell complex

One may choose to triangulate the sphere and then add the string (first image). A more efficient way is to cut the sphere into two hemispheres (second image). Turns out, one can remove one of the edges and merge the hemispheres. One $2$-cells is enough (third image).

Cells and their boundaries: $$\dim 2: {\tau}, {\partial}_2{\tau} = a - a = 0;$$

$$\dim 1: a, c, {\partial}_1a = B - A, {\partial}_1c = B - A;$$

$$\dim 0: A, B, {\partial}_0A = 0, {\partial}_0B = 0.$$

Step 2: find the chain groups

$$C_2(K) = {\rm \hspace{3pt} span \hspace{3pt}}\{\tau \} = {\bf R},$$ $$C_1(K) = {\rm \hspace{3pt} span \hspace{3pt}}\{a, c \} = {\bf R}^2,$$ $$C_0(K) = {\rm \hspace{3pt} span \hspace{3pt}}\{A, B \} = {\bf R}^2.$$

Step 3: find the matrices of the boundary operators

$${\partial}_2: C_2(K) {\rightarrow} C_1(K), {\bf R} {\rightarrow} {\bf R}^2,$$

$${\partial}_2 = [0, 0]^T = \left| \begin{array}{} 0 \\ 0 \end{array} \right| ; $$

$${\partial}_1: C_1(K) {\rightarrow} C_0(K), {\bf R}^2 {\rightarrow} {\bf R}^2,$$

$${\partial}_1 = \left| \begin{array}{rr} -1 & -1 \\ 1 & 1 \end{array} \right| ;$$

$${\partial}_0: C_0(K) {\rightarrow} 0, {\bf R}^2 {\rightarrow} 0,$$ $${\partial}_0 = [0, 0]^T = \left| \begin{array}{} 0 \\ 0 \end{array} \right|.$$

Chain complex:

$$0 {\rightarrow} C_0(K) {\rightarrow} C_0(K) {\rightarrow} C_0(K) {\rightarrow} 0.$$

Step 4: find the cycle groups

$${\partial}_2 = 0 \rightarrow Z_2(K) = \ker {\partial}_2 = C_2(K) = {\rm \hspace{3pt} span \hspace{3pt}} \{\tau \}.$$

$${\partial}_1a = {\partial}_1c = B - A \rightarrow {\partial}_1(a - c) = 0 \rightarrow a - c{\in}Z_1(K).$$

rank ${\partial}_1 = 1 \rightarrow Z_1(K) = {\rm \hspace{3pt} span \hspace{3pt}}\{a - c \}$.

$${\partial}_0 = 0 \rightarrow Z_0(K) = \ker {\partial}_0 = C_0(K) = {\rm \hspace{3pt} span \hspace{3pt}} \{A, B \}$$

Step 5: find the boundary groups

$$B_2(K) = {\partial}_3(0) = 0,$$ $$B_1(K) = {\rm \hspace{3pt} span \hspace{3pt}} \{{\partial}_2({\tau}) \} = {\rm \hspace{3pt} span \hspace{3pt}} \{0 \} = 0,$$ $$B_0(K) = {\rm \hspace{3pt} span \hspace{3pt}} \{{\partial}_1(a), {\partial}_1(c) \} = {\rm \hspace{3pt} span \hspace{3pt}} \{B - A, B - A \} = {\rm \hspace{3pt} span \hspace{3pt}} \{B - A \}.$$

Step 6: find the homology groups

$$H_2(K) = Z_2(K) / B_2(K) = {\rm \hspace{3pt} span \hspace{3pt}} \{{\tau} \} / 0 = {\rm \hspace{3pt} span \hspace{3pt}} \{{\tau} \};$$

$$H_1(K) = Z_1(K) / B_1(K) = {\rm \hspace{3pt} span \hspace{3pt}} \{a - c \} / 0 = {\rm \hspace{3pt} span \hspace{3pt}} \{a - c \};$$

$$H_0(K) = Z_0(K) / B_0(K) = {\rm \hspace{3pt} span \hspace{3pt}} \{A, B \} / {\rm \hspace{3pt} span \hspace{3pt}} \{B - A \} = {\rm \hspace{3pt} span \hspace{3pt}} \{A \}.$$