Combinatorial cell complexes

Gluing cells together

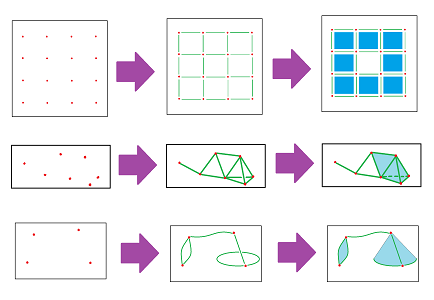
With such a tool as the quotient available to us, we can construct anything imaginable starting from almost anything. We would like, however, to learn how to build things from the elementary pieces, cells, and do it in a gradual and orderly manner.

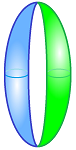
One can see examples of things created from elementary pieces appear in real life, such as these balls sewn (or otherwise formed) from patches of leather:

In either of these examples, we orderly glue edges to each other at their endpoints. But, those endpoints are $0$-cells. Furthermore, we glue $2$-cells to each other along their edges. And, those edges are $1$-cells. And so on.

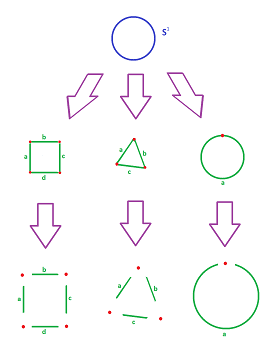
Example (circle). The simplest cubical complex we could use to represent the circle consists of four edges arranged in a square. But why should we need four pieces when we know that a circle can be built from a single segment with the endpoints glued together? In fact, the number one example of identification is gluing the endpoints of a segment to create a circle. The latter will have just one $1$-cell in contrast to the realizations we have seen, i.e., $4$ for a cubical complex and $3$ for a simplicial complex:

$\square$

We are already familiar with gradual and orderly building -- via skeleta -- of cubical and simplicial complexes:

The only difference is that now we have more flexibility about the cells. They are balls of various dimensions:

Definition. A (closed) $n$-cell $a$ is a topological space homeomorphic to the closed $n$-ball $${\bf B}^n:=\{x\in {\bf R}^n:\ ||x|| \le 1 \}.$$ The image of the frontier of ${\bf B}^n$ in ${\bf R}^n$ under this homeomorphism $h:{\bf B}^n \to a$ is called the boundary of the cell $$\partial a := h(\operatorname{Fr}({\bf B}^n)).$$ Also, the image of the interior, and the complement of the boundary, is denoted by $$\dot{a} := a \setminus \partial a,$$ and may simply be called the “interior” of the cell.

Proposition. The definition of the boundary is topological in the sense that under homeomorphisms of cells, boundary is mapped to boundary.

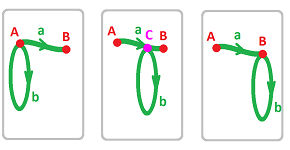
Example (ladle). Let's consider a specific example. Suppose we want to build something that looks like a ladle, which is the same topologically as a Ping-Pong bat:

We want to build a simple topological space from the ground up, using nothing but cells attached to each other in the order of increasing dimensions. In our box, we have: the parts, the glue, the schematics, and a set of instructions of how to build it.

Here is the schematics:

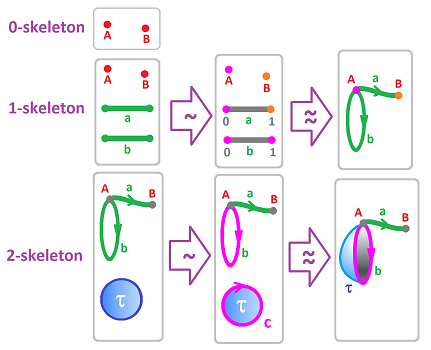
Let's narrate the instructions. We start with the list $K$ of all cells arranged according to their dimensions:

• dimension $0$: $A,B$;
• dimension $1$: $a,b$;
• dimension $2$: $\tau$. $\\$

These are the building blocks. At this point, they may be arranged in a number of ways.

Now, the two points $A,B$ are united into one topological space -- as the disjoint union. That's the $0$-skeleton $K^{(0)}$ of $K$.

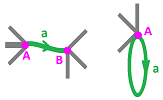
Next, we take this space $K^{(0)}$ and combine it, again as the disjoint union, with all $1$-cells in $K$. To put them together, we introduce an equivalence relation on this set. But, to keep this process orderly, we limit ourselves to an equivalence relation between the vertices (i.e., the elements of $K^{(0)}$, and the boundaries of the $1$-cells we are adding. In other words, we identify the endpoints of $a$ and $b$ to the points $A$ and $B$. This can happen in several ways. We make our choice by specifying the attaching map for each $1$-cell thought of as a segment $[0,1]$: $$f_a:\partial a\to K^{(0)},\ f_b:b\to K^{(0)} ,$$ by specifying the values on the endpoints: $$f_a(0)=A,\ f_a(1)=B,\ f_b(0)=A,\ f_b(1)=A.$$ We use these maps following the attaching rule: $$x\sim y \Longleftrightarrow f_a(x)=y.$$ The result is the $1$-skeleton $K^{(1)}$.

The rule we have followed is to choose

an equivalence relation on the last skeleton combined with the boundaries of the new cells.

Next, we take this space $K^{(1)}$ and combine it, again as the disjoint union, with all $2$-cells in $K$. To put them together, we introduce an equivalence relation following the rule above. For this dimension, we identify the edge of $\tau$ with a $1$-cell $a$, point by point. This can happen in several ways and we make our choice by specifying the attaching map for the $2$-cell: $$f_{\tau}:\tau\to K^{(1)} .$$ We only need to specify the values on the boundary and we assume that $f_{\tau}:\partial\tau\to b$ is a homeomorphism. We again use the attaching rule: $$x\sim y \Longleftrightarrow f_{\tau}(x)=y.$$ The result is the $2$-skeleton $K^{(2)}$, which happens to be the realization of the whole $K$. $\square$

Exercise. Present cell complex structures for these two arrangements:

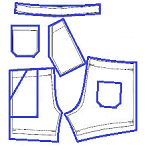
Exercise. (a) Present a cell complex structure for the sewing pattern below (shorts). (b) Do the same for a pair of breakaway pants.

The formal definition of cell complex does not rely on illustrations. It is inductive.

Definition. Suppose we have a finite collection of (unrelated to each other) cells $K$. Suppose $C^n$ denotes the set of all $n$-cells in $K$. Next, the $0$-skeleton $K^{(0)}$ is defined as the disjoint union of all $0$-cells: $$K^{(0)} = \bigsqcup C^0 .$$

Now suppose that the $n$-skeleton $K^{(n)}$ has been constructed. Then the $(n+1)$-skeleton $K^{(n+1)}$ is constructed as follows. Suppose for each $(n+1)$-cell $a$, there is an attaching map $$f_a : \partial a \to K^{(n)}.$$ Then the $(n+1)$-skeleton $K^{(n+1)}$ is defined as the quotient of the disjoint union of the $n$-skeleton $K^{(n)}$ and all the $(n+1)$-cells: $$K^{(n+1)} = (K^{(n)} \bigsqcup C^{n+1})/ _{\sim},$$ with $\sim$ defined by the following condition:

$x \sim f_a(x)$ for all $x \in \partial a$ and all $a \in C^{n+1}$.

The attaching maps must satisfy an extra condition:

the image $f_a(\partial a)$ is the union of a collection of $n$-cells of $K$.

Furthermore, we can assume without loss of generality that the attaching map is extended to $$f_a : a \to K^{(n)},$$ with the only requirement:

• $f_a\Big|_{\dot{a}}$ is a homeomorphism. $\\$

In fact, this map may be seen as a restriction of the identification map. Further, with the inclusions of the skeleta into the complex provided, the attaching map can also be thought of as $$f_a : a \to |K|.$$

Thus, a cell complex $K$ is a combination of the following:

• 1. the collection of cells $K$,
• 2. the skeleta $K^{(0)} \subset K^{(1)} \subset \ ... \ \subset K^{(N)}=|K|$, and
• 3. the attaching maps $f_a:a\to K^{(n)}$, for each $a$ an $n$-cell in $K$. $\\$

If this was a building, these three would be the inventory, the blueprints, and the daily work orders.

Exercise. Provide an illustration similar to the one above for a topological space that looks like (a) an air-balloon with a thread hanging, (b) a candy apple.

Exercise. Find the cell complex representation of the figure eight.

Exercise. Represent the sphere as a cell complex with two $2$-cells, list all cells, and describe/sketch the gluing maps.

Algebra

The way we attach the cells to each other is purposeful. Remember we want to be able to compute the boundary operator in just as orderly a fashion as we build the cell complex. This is the reason why we never attach $k$-cells to other $k$-cells but -- along their boundaries -- to the preexisting $(k-1)$-cells:

the image $f_a(\partial a)$ of an $n$ cell is the union of a collection of $(n-1)$-cells of $K$.

Note that, without this extra constraint, the result may look very different from what we expect:

The middle option is unacceptable.

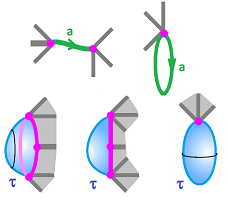
Let's illustrate the acceptable attaching maps.

A $1$-cell may be attached to $0$-cells as a rope or as a noose:

Meanwhile, a $2$-cell may be attached to $1$-cells as a soap film, a zip-lock bag, or an air-balloon.

For either dimension, the first of these attaching maps is a homeomorphism and the last is constant. Generally, a cell can be attached along its boundary in a number of ways that include collapses to lower dimensional cells.

The point of the extra constraint on attaching maps is to allow us to proceed directly to algebra as shown below. If the (topological) boundary of an $(n+1)$-cell $\tau$ is the union of several $n$-cells $a, b, c, ...$: $$\partial \tau = a \cup b \cup c \cup ...,$$ then the boundary operator evaluated at $\tau$ is some linear combination of these cells: $$\partial _{n+1}(\tau) = \pm a\pm b\pm c\pm...$$

What are the signs? They are determined by the orientation of the cell $\tau$ as it is placed in the cell complex and attached to its $n$-cells. Let's consider this matching in lower dimensions.

In dimension $1$, the meaning of orientation is simple. It is the direction of the $1$-cell as we think of it as a parametric curve. Then the boundary is the last vertex it is attached to minus the first vertex.

Here, if the (topological) boundary of the $1$-cell $a$ is identified, by the attaching maps, with the union of two $0$-cells $A, B$ (or just $A$), while the (algebraic) boundary of $a$ is the sum (or a linear combination) of $A, B$: $$\begin{array}{lllllll} f_a(\partial a) &= \{A,B\} &\leadsto &\partial _1 (a) = B-A;\\ f_a(\partial a) &= \{A\} &\leadsto &\partial _1 (a) = A-A=0. \end{array}$$

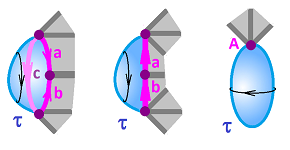
For a $2$-cell, a direction is chosen for its circular boundary, clockwise or counterclockwise. As we move along the boundary following this arrow, we match the direction to that of each $1$-cell we encounter:

Here, we have three cases: $$\begin{array}{lllllll} f_{\tau}(\partial \tau) &= a \cup b \cup c &\leadsto& \partial _2\tau &= a - b - c;\\ f_{\tau}(\partial \tau) &= a \cup b &\leadsto& \partial _2\tau &= -a - b +a+b=0;\\ f_{\tau}(\partial \tau) &= A &\leadsto & \partial _2\tau &= 0. \end{array}$$

Initially, we can understand the orientation of a cell as an ordering of its vertices, just as we did for simplicial complexes.

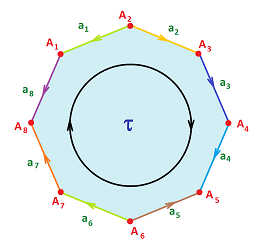
Example. Let's evaluate the boundary operator for this $2$-cell, with the orientations of $1$-cells randomly assigned.

We have: $$\partial \tau = -a_1 + a_2 + a_3 + a_4 - a_5 + a_6 + a_7 - a_8.$$ Further, $$\begin{array}{llll} \partial (\partial \tau) &=& \partial( -a_1 + a_2 + a_3 + a_4 - a_5 + a_6 + a_7 - a_8 ) \\ &=& -\partial a_1 + \partial a_2 + \partial a_3 + \partial a_4 - \partial a_5 + \partial a_6 + \partial a_7 - \partial a_8 \\ &=& -(A_1 - A_2) + (A_3 - A_2) + (A_4 - A_3) + (A_5 - A_4) \\ && - (A_5 - A_6) + (A_7 - A_6) + (A_8 - A_7) - (A_8 - A_1) \\ &=& 0. \end{array}$$$\square$

Theorem. The $k$th homology of a cell complex is fully determined by its $(k+1)$-skeleton.

Exercise. Prove the theorem.

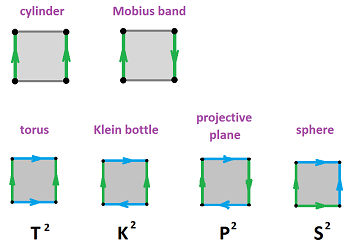
What we can make from a square

Let's see what we can construct from the square by gluing one or two pairs of its opposite edges. We will compute the homology of these surfaces:

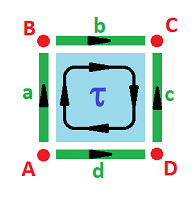
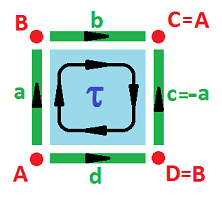
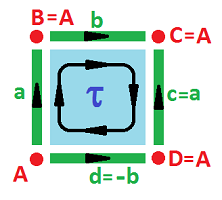
Example (square). Here is the simplest cell complex representation of the square (even though the orientations can be arbitrarily reversed):

The complex $K$ of the square is:

• $0$-cells: $A, B, C, D$;
• $1$-cells: $a, b, c, d$;
• $2$-cells: $\tau$;
• boundary operator: $\partial \tau = a + b + c - d; \ \partial a = B-A, \partial b = C-B$, etc. $\square$

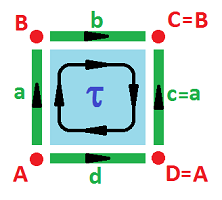
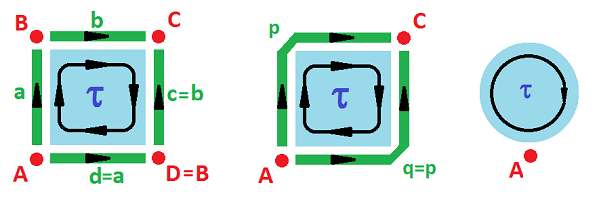
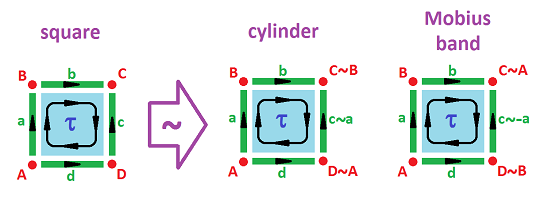
Example (cylinder). We can construct the cylinder $C$ by gluing two opposite edges with the following equivalence relation: $(0,y) \sim (1,y)$. The result of this equivalence relation of points can be seen as equivalence of cells: $$a \sim c;\ A \sim D,\ B \sim C.$$

We still have our collection of cells (with some of them identified as before) and only the boundary operator is different:

• $\partial \tau = a + b + (-a) - d = b - d ;$
• $\partial a = B-A,\ \partial b = B-B=0,\ \partial d = A-A = 0.$ $\\$

The chain complex is $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_2 & \ra{\partial} & C_1 & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b,d > & \ra{?} & < A,B > \\ & & \tau & \mapsto & b - d \\ & & & & a & \mapsto & B-A \\ & & & & b & \mapsto & 0 \\ & & & & d & \mapsto & 0 \\ {\rm kernels:} & & Z_2 = 0 && Z_1 = < b,d > & & Z_0 = < A,B > \\ {\rm images:} & & B_2 = 0 && B_1 = < b - d > & & B_0 = < B-A > \end{array}$$ Here, “kernels” are the kernels of the maps to their right, “images” are the images of the maps to their left.

So, the homology is identical to that of the circle! $\square$

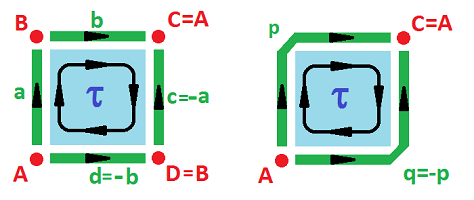
Example (Möbius band). In order to build the Möbius band ${\bf M}^2$, we use the equivalence relation: $(0,y) \sim (1,1-y)$. Once again, we can interpret the gluing as equivalence of cells, $a$ and $c$. But this time they are attached to each other with $c$ upside down. It makes sense then to interpret this as equivalence of cells but with a flip of the sign: $$c \sim -a.$$ Here $-c$ represents edge $c$ with the opposite orientation:

In other words, this is an equivalence of chains. Further, $$A \sim D, \ B \sim C.$$ The boundary operator is:

• $\partial \tau = a + b - (-a) - d = 2a + b - d;$
• $\partial a = B-A, \ \partial b = A-B, \ \partial d = B-A.$ $\\$

The chain complex is $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_2 & \ra{\partial} & C_1 & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b,d > & \ra{?} & < A,B > \\ & & \tau & \mapsto & 2a + b - d \\ & & & & a & \mapsto & B-A \\ & & & & b & \mapsto & A-B \\ & & & & d & \mapsto & B-A \\ {\rm kernels:} & & Z_2 = 0 && Z_1 = < a+b,a-d > & & Z_0 = < A,B > \\ {\rm images:} & & B_2 = 0 && B_1 = < 2a+b-d > & & B_0 = < B-A > \end{array}$$ $\square$

Example (sphere). We can either build the sphere as a quotient of the square or, easier, we just combine these pairs of the consecutive edges:

Then we have only two edges left. Even better, the last option gives us a complex with no $1$-cells whatsoever! $\square$

Example (projective plane). The projective plane comes from a certain quotient of the disk, ${\bf B}^2/_{\sim}$, where $u \sim -u$ is limited to the boundary of the disk. It can also be seen as a quotient of the square:

As we see, the edge of the disk is glued to itself, with a twist. Its algebraic representation is almost the same as before: $p\sim -p$.

• $2$-cells: $\tau$ with $\partial\tau = 2p$;
• $1$-cells: $p$ with $\partial p = 0$;
• $0$-cells: $A$ with $\partial A = 0$.

For these three different rings: $$\begin{array}{llllll} H_1({\bf P}^2; {\bf Z}) &= < p > / < 2p > &= {\bf Z} / 2{\bf Z} &\cong {\bf Z}_2 ,\\ H_1({\bf P}^2;{\bf Z}_2) &= < p > / < 2p > &= < p > / 0 &\cong {\bf Z}_2 ,\\ H_1({\bf P}^2;{\bf R}) &= \operatorname{span}(p) / \operatorname{span}(2p) &= \operatorname{span}(p) / \operatorname{span}(p) &\cong 0. \end{array}$$

$$\begin{array}{llllllll} {\bf Z}: \quad &\partial \tau = 2p & &&\Longrightarrow &\text{so what?}\\ {\bf Z}_2: \quad &\partial \tau = 2p &\Longrightarrow &\partial \tau = 0 &\Longrightarrow &\tau \text{ is a cycle, so what?}\\ {\bf R}:\quad &\partial \tau = 2p &\Longrightarrow &\partial \Big(\tfrac {1}{2}\tau \Big)=p &\Longrightarrow &p \text{ is a boundary!} \end{array}$$

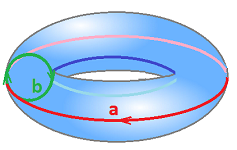
Example (torus). What if after creating the cylinder by identifying $a$ and $c$ we then identify $b$ and $d$? Like this: $$c \sim a,\ d \sim -b.$$ The result is the torus ${\bf T}^2$:

Note how all the corners of the square come together in one. Then the chain complex has very few cells to deal with: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_2 & \ra{\partial} & C_1 & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b > & \ra{?} & < A > \\ & & \tau & \mapsto & 0 \\ & & & & a & \mapsto & 0 \\ & & & & b & \mapsto & 0 \\ {\rm kernels:} & & Z_2 = < \tau > && Z_1 = < a,b > & & Z_0 = < A > \\ {\rm images:} & & B_2 = 0 && B_1 = 0 & & B_0 = 0 \end{array}$$

$\square$

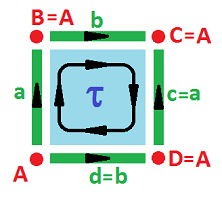
Example (Klein bottle). What if we flip one of the edges before gluing? Like this: $$c \sim a,\ d \sim -b.$$

The corners once again come together in one and the chain complex has very few cells to deal with: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_2 & \ra{\partial} & C_1 & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b > & \ra{?} & < A > \\ & & \tau & \mapsto & 2a \\ & & & & a & \mapsto & 0 \\ & & & & b & \mapsto & 0 \\ {\rm kernels:} & & Z_2 = 0 && Z_1 = < a,b > & & Z_0 = < A > \\ {\rm images:} & & B_2 = 0 && B_1 = < 2a > & & B_0 = 0 \end{array}$$ Thus, unlike the two tunnels in the torus, this time there is only one and the other topological feature is a twist. $\square$

This is how we can construct $3$-dimensional complexes. We start with a cube. First, we glue its top and bottom, with each point identified to the one directly underneath. Then we cut the cube into two by a horizontal square.

Then we consider the relations listed above to identify the edges of this square, just as we did for the torus, etc. These relations tell us how the opposite faces of the cube are glued together.

The $n$-dimensional balls and spheres

Cell complexes use very few cells in comparison to cubical and simplicial complexes but the trade-off is the complexity of some of the concepts we will need. In order to develop a complete theoryfor cell complexes, we have to add one missing part: we would need to figure out the meaning of orientation of cells, beyond dimension $2$. With that, we would be able to define the boundary operator $\partial :C_n\to C_{n-1}$ and to prove the property that makes all of this work: $\partial\partial =0$. We will omit these steps and rely, informally, on what we have already developed.

The issue of orientation has been previously developed in full for the following cases:

• $K$ is a cubical complex, and
• $K$ is a simplicial complex. $\\$

In addition, the issue is simply moot when

• $K$ is any cell complex but the ring of coefficients is $R={\bf Z}_2$.

For the general cell complexes and arbitrary coefficients, there are two simple enough cases that we can handle. They appear in the highest dimension $n=\dim K$. For an $n$-cell $\sigma$, we have:

• $\partial _n(\sigma)=0$ when there are no $(n-1)$-cells in $\partial \sigma$;
• $\partial _n(\sigma)=\pm s$ when $s$ is the $(n-1)$-cell in $K$ that forms the boundary $\partial \sigma$ of $\sigma$, and the sign is “+” when there are no other $n$-cells adjacent to $s$.

We use these two cases to compute the chain complexes of the $n$-ball ${\bf B}^n$ and the $(n-1)$-sphere ${\bf S}^{n-1},\ n>2$.

Example (balls). We represent ${\bf B}^n$ as a cell complex as follows.

Cells:

• $n$-cells: ${\sigma}$,
• $(n-1)$-cells: $a$,
• $0$-cells: $A$. $\\$

The boundary operator:

• ${\partial}{\sigma} = a,$
• ${\partial}a = 0,$
• ${\partial}A = 0.$

The chain complex and the computation of homology are below: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccccccccccccc} & C_n & \ra{\partial} & C_{n-1} & \ra{\partial} & C_{n-2} & \to ... \to & C_0 \\ & < \sigma > & \ra{\cong} & < a > & \ra{0} & 0 & \to ... \to & < A > \\ & {\sigma} & \mapsto & a & \mapsto & 0 & & A & \\ {\rm kernels:} & Z_n = 0 & & Z_{n-1} = < a > & & Z_{n-2} = 0 & ... & Z_0 = < A > \\ {\rm images:} & B_n = 0 & & B_{n-1} = < a > & & B_{n-2} = 0 & ... & B_0 = 0 &\square \end{array}$$ %$\square$

Example (spheres). The sphere ${\bf S}^{n-1}$ has the same cell complex representation as the ball except the $n$-cell is missing.

The cells:

• $(n-1)$-cells: $a$,
• $0$-cells: $A$. $\\$

The boundary operator:

• ${\partial}a = 0,$
• ${\partial}A = 0.$

The chain complex and homology are: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccccccc} & C_n & \ra{\partial} & C_{n-1} & \ra{\partial} & C_{n-2} & \to ... \to & C_0 \\ & 0 & \ra{0} & < a > & \ra{0} & 0 & \to ... \to & < A > & \\ & & & a & \mapsto & 0 & & A & \\ {\rm kernels:} & Z_n = 0 & & Z_{n-1} = < a > & & Z_{n-2} = 0 & ... & Z_0 = < A > \\ {\rm images:} & B_n = 0 & & B_{n-1} = 0 & & B_{n-2} = 0 & ... & B_0 = 0 &\quad\square \end{array}$$ %$\square$

Quotients of chain complexes

Next, we explore how to compute the chain complex and the homology groups of a cell complex in the way it is built -- gradually.

Example (circle). Recall how we computed the homology of the circle. Its chain complex is $$\partial = 0 \colon C_1 = < a > \to C_0 =< A >.$$ Then it follows that $$H_1 = < a > \cong {\bf Z}, \ H_0 = < A > \cong {\bf Z}.$$ The cell complex is built from the segment via the quotient construction, point-wise or cell-wise. But we have also seen examples when these identifications are interpreted algebraically, chain-wise.

Let's follow this alternative route. We assume that we initially have the (cubical) complex $K$ of the segment:

• $0$-cells: $A, B$,
• $1$-cells: $a$,
• boundary operator: $\partial a = B-A$. $\\$

Its chain complex is $$\partial : C_1(K)=< a > \to C_0(K)=< A,B >.$$ Now to build the circle, we identify $A$ and $B$, $A \sim B$, but this time not as points but as $0$-chains. The outcome of this construction is not the quotient of topological space $|K|$ or even of cell complex $K$ but the quotient of the chain group $C_0(K)$! The result is easy to present and compute algebraically: $$C_0 (K) / _{\sim} = < A,B > / < A-B > = < A,B|A=B > \cong < A >.$$ The new boundary operator is the quotient of the old and it is trivial: $$\partial' =q\partial =0: C_1(K)=< a > \to C_0(K)/ _{\sim} = < A >.$$ Here $q$ is the identification function of this equivalence relation. It immediately follows that $$H_0=< A >.$$

Meanwhile, since $C_1=< a >$, we have the homology: $$H_1=\ker \partial _1= < a > \cong {\bf R}.$$ That the hole!

The results are the same as that of the original analysis. $\square$

Things are more complicated in higher dimensions.

Example (cylinder). Let's make the cylinder from the square, algebraically.

The complex $K$ of the square is:

• $0$-cells: $A, B, C, D$;
• $1$-cells: $a, b, c, d$;
• $2$-cells: $\tau$;
• boundary operator: $\partial (\tau) = a + b - c - d;\ \partial (a) = B-A,\ \partial (b) = C-B,\ \partial (c) = C-D$, etc.

We construct a chain complex for the cylinder by identifying a pair of opposite $1$-cells: $$a \sim c.$$ This produces the quotients of the chain groups of $K$ since $a$ and $c$ are their generators.

Now the quotients of the boundary operators between these quotients are to be considered: $$[\partial _n]: C_n(K) / _{\sim} \to C_{n-1}(K) / _{\sim}.$$ As was discussed previously, the quotient of an operator is well-defined only if the operator maps equivalence classes to equivalence classes; i.e., this diagram commutes: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{cccccccccc} C_n(K) & \ra{\partial _n} & C_{n-1}(K) \\ \da{q} & & \da{q} \\ C_n(K) / _{\sim} & \ra{[\partial _n]} & C_{n-1}(K) / _{\sim} \end{array}$$ Here, $q$ is the identification function. So, for $n=1$, the equivalence of edges forces the equivalence of vertices: $$A \sim D, B \sim C.$$ The relations are illustrated below:

We compute the quotients of the chain groups: $$\begin{array}{ll} C_2(K) / _{\sim} = < \tau >;\\ C_1(K) / _{\sim} = < a,b,c,d > / < a-c > = < [a],[b],[d] >;\\ C_0(K) / _{\sim} = < A,B,C,D > / < A-D,B-C > = < [A],[B] >. \end{array}$$

Then we compute the values of the quotients of the boundary operators: $$\begin{array}{lllllll} &[\partial_2](\tau) &= [\partial_2(\tau)]&= [a + b - c - d] &= [b - d];\\ &[\partial_1]([a]) &= [\partial_1(a)]& &= [B-A];\\ &[\partial_1]([b]) &= [\partial_1(b)]& = [C-B] &= 0;\\ &[\partial_1]([d]) &= [\partial_1(d)] &= [D-A] &= 0. \end{array}$$

Now, these operators and groups form a chain complex and we compute its homology: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & < \tau > & \ra{[\partial _2]} & < [a],[b],[d] > & \ra{[\partial _1]} & < [A],[B] >\\ {\rm kernels:} & & Z_2 = 0 && Z_1 = < [b],[d] > & & Z_0 = < [A],[B] > \\ {\rm images:} & & B_2 = 0 && B_1 = < [b - d] > & & B_0 = < [B-A] >

\end{array}$$ The results are the same as before. $\square$

Exercise. Verify the claims made in the above example:

• the quotient operators are well-defined;
• the square diagram above is commutative for all $n$;
• the sequence of quotient groups is a chain complex.

Exercise. Provide such a computation for the Möbius band.

The approach is applicable to any cell complex $K$. As we build the complex $K$ skeleton-by-skeleton: $$K^{(0)} \leadsto K^{(1)} \leadsto ...\leadsto K^{(N)} = K,$$ we also build the chain complex for $K$ step-by-step as follows. $$C(K^{(0)}) \leadsto C(K^{(1)}) \leadsto ...\leadsto C(K^{(N)}) = C(K).$$ For each $n=1,2,…,N$, the attaching maps yield equivalence relations. Each $n$-cell $\sigma$ to be added to $K^{(n)}$ is treated as a generator to be added to $C(K^{(n)})$ because its boundary $(n-1)$-cells are already present. Then the current chain groups (and the boundary operators) of $K$ are modified via quotient modulo subgroups generated by these boundary cells of $\sigma$.

Exercise. Use this approach to compute the chain complex of the double banana:

Exercise. Use this approach to compute the chain complexof the “book with $n$ pages”:

Triangulations of manifolds

Next, we study manifolds represented by data; given a simplicial complex $K$, what are the necessary and sufficient conditions that its realization $|K|$ is an $n$-manifold $M^n$ (without boundary)? When this is the case, we will call $K$ a combinatorial $n$-manifold.

First, let's take care of the point-set topological issues. Since the realization is the union of finitely many $n$-balls and, therefore, second-countable, then so is $|K|$. For Hausdorff, two points are either in the same cell, which is itself Hausdorff, or in two disjoint stars, which serve as the required disjoint neighborhoods.

Exercise. Provide the details of this proof and state the theorem.

So, we only need to deal with the question whether $|K|$ is locally Euclidean: does every point in $M^n$ have a neighborhood homeomorphic to ${\bf R}^n$?

The first observation is simple.

Theorem. If $|K|\approx M^n$ then $\dim K =n$.

Now, suppose we have an $n$-dimensional simplicial complex $K$. How do we know that $K$ is a combinatorial $n$-manifold? Can we answer this question just by examining the list of simplices of $K$? The answer is Yes.

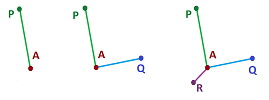
We start with dimension $n=1$. We could use the two “global” results given previously, but instead we start from the definition. First, by the above theorem, $K$ has to be a graph. Furthermore, the star of a vertex with more than one adjacent edge isn't homeomorphic to the open interval; that's why we require:

• each vertex is shared by exactly two edges.

The condition can be restated in terms of vertices only.

Theorem. A graph $K$ is a combinatorial $1$-manifold if and only if the following condition is satisfied:

• (A1) for any vertex $A\in K$, there are exactly two vertices $P,Q\in K$ with $AP, AQ\in K$.

Next, dimension $n=2$. The first requirement a complex has to meet to be a surface is similar to the one above:

• each edge is shared by exactly two faces.

Once again, this condition can fail in three ways:

• an edge isn't contained in any face,
• an edge is contained in exactly one face,
• an edge is shared by more than two faces. $\\$

In the first case, we might have a curve. In the second, possibly, a surface with boundary.

Exercise. To justify the above statement, prove that three copies of ${\bf R}^n_+$ glued together by the hyperplane $\{x_1=0\}$ is not homeomorphic to ${\bf R}^n$. Hint: same as idea as for “T” $\not\approx$ “I”.

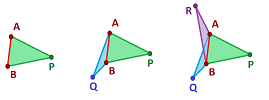
Now, we restate this condition combinatorially, i.e., for a $2$-dimensional simplicial complex $K$ given by a list vertices and simplices as sets of vertices: $$K=\{A,B,C, ...,AB,BC, ...,ABC, ...\}.$$ In terms of these sets, every face is a triple, such as $ABC$, and every edge is a double, such as $AB$. The above condition can then be rephrased in terms $K$:

• (A2) for any edge $AB\in K$, there are exactly two vertices $P,Q\in K$ with $ABP, ABQ \in K$.

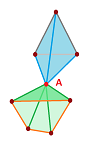
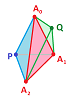
This condition does not guarantee that the realization of $K$ is a surface, as the image below shows.

As we can see, condition (A2) is satisfied here for all edges but the vertex in the middle does not have a neighborhood homeomorphic to the disk.

Exercise. To justify the above statement, prove that two copies of ${\bf R}^n$ glued together by the origin $0$ is not homeomorphic to ${\bf R}^n$.

Then we have to require that the faces around each vertex are arranged in, and can be listed as, a circular fashion to form a disk-like subcomplex.

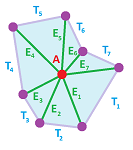
Given a vertex $A$ the faces (triangles) that contain $A$ must form a “cycle”:

$T_1$ glued to $T_2$ glued to $T_2$ ... $T_m$ glued to $T_1$.

We can state this as a condition on faces:

• For each vertex $A$, suppose
  • all edges that contain $A$ are $E_1, E_2, ..., E_k$, and
  • all triangles that contain $A$ are $T_1, T_2, ..., T_m$.
• Then $k=m$ and the two sets can be reindexed in such a way that:
  • $E_1$ is shared by $T_1, T_2$;
  • $E_2$ is shared by $T_2, T_3$;
  • ...
  • $E_m$ is shared by $T_m, T_1$. $\\$

Of course, we recognize this collection of simplices as the star of vertex $A$.

Restated in terms of subsets of $K=\{A, B, C, ...\}$, the above condition will take the following form:

• (B2) for each vertex $A\in K$, the set of adjacent vertices $\{B\in K: AB \in K \}$ can be represented as $\{B_1, B_1, ..., B_m\}$ with

$$AB_1B_2, AB_2B_3, ..., AB_mB_1 \in K.$$ We have proved the following.

Theorem. A $2$-dimensional simplicial complex $K$ is a combinatorial $2$-manifold if and only if it satisfies conditions (A2) and (B2).

Exercise. Is this a triangulation of the projective plane?

Exercise. Prove an analog of the above theorem for manifolds with boundary.

Exercise. When is a cubical complex in ${\mathbb R}^3$ a surface?

The reason why we impose these conditions on a complex is clear now: we have to check that the star of every simplex of every dimension forms an $n$-ball. The difficulty is that there will be $n$ such conditions and we will have to set them up one at a time for each dimension from $0$ to $n$. Let's consider just one of them.

In light of our discussion of conditions (A1) and (A2), the easiest way things can go wrong is when three pieces that are already homeomorphic to the $n$-ball are glued to each other. In other words, if an $(n-1)$-simplex is shared by three distinct $n$-simplices, this is not an $n$-manifold.

Condition (A3) is illustrated below:

Unlike the theorem above for $n=2$, the next one gives us only a necessary condition.

Theorem. If $K$ is a combinatorial $n$-manifold then the following condition holds:

• (A$n$) if $A_0A_1...A_{n-1}\in K$ then there are exactly two vertices $P,Q\in K$ with

$$A_0A_1 ...A_{n-1}P\in K \quad \text{and}\quad A_0A_1 ...A_{n-1}Q\in K .$$

What conditions (A1),(A2), ...,(A$n$) have in common is not the dimensions of these cells but rather their codimensions: $$\operatorname{codim} \sigma:=n-\dim \sigma.$$ These conditions are about cells of codimension $1$.

Exercise. Suggest condition (B3) and illustrate it with a sketch. Hint: what's the codimension?

Exercise. Give an example of a simplicial complex that satisfies conditions (A3) and (B3) but is not a combinatorial $3$-manifold.