This site is being phased out.
Chain complexes
Contents
Modules
We now review what it takes to have arbitrary ring of coefficients $R$.
Recall that
- with $R={\bf Z}$, the chain groups are abelian groups,
- with $R={\bf R}$ (or other fields), the chain groups are vector spaces, and now
- with an arbitrary $R$, the chain groups are modules.
Informally,
The following definitions and results can be found in the standard literature such as Hungerford, Algebra (Chapter IV).
Definition. Given a commutative ring $R$ with the multiplicative identity $1_R$, a (commutative) $R$-module $M$ consists of an abelian group $(M, +)$ and a scalar product operation $R \times M \to M$ such that for all $r,s \in R$ and $x, y \in M$, we have:
- $r(x+y) = rx + ry$,
- $(r+s)x = rx + sx$,
- $(rs)x = r(sx)$,
- $1_Rx = x$. $\\$
The scalar multiplication can be written on the left or right.
If $R$ is a field, an $R$-module is a vector space.
The rest of the definitions are virtually identical to the ones for vector spaces.
A subgroup $N$ of $M$ is a submodule if it is closed under scalar multiplication: for any $n \in N$ and any $r\in R$, we have $rn \in N$.
A group homomorphism $f: M \to N$ is a (module) homomorphism if it preserves the scalar multiplication: for any $m,n \in M$ and any $r, s \in R$, we have $f(rm + sn) = rf(m) + sf(n)$. When $R$ is a division ring, $f$ is called a linear operator.
A bijective module homomorphism is an (module) isomorphism, and the two modules are called isomorphic.
We will need the following classification theorem as a reference.
Theorem (Fundamental Theorem of Finitely Generated Abelian Groups). Every finitely generated abelian group $G$ is isomorphic to a direct sum of primary cyclic groups and infinite cyclic groups: $${\bf Z}^n \oplus {\bf Z}_{q_1} \oplus ... \oplus {\bf Z}_{q_s},$$ where $n \ge 0$ is the rank of $G$ and the numbers $q_1, ...,q_s$ are powers of (not necessarily distinct) prime numbers. Here ${\bf Z}^n$ is the free part and the rest is the torsion part of $G$.
The kernel of a module homomorphism $f : M \to N$ is the submodule of $M$ consisting of all elements that are taken to zero by $f$. The isomorphism theorems of group theory are still valid.
A module $M$ is called finitely generated if there exist finitely many elements $v_1,v_2, ...,v_n \in M$ such that every element of $M$ is a linear combination of these elements (with coefficients in $R$).
A module $M$ is called free if it has a basis. This condition is equivalent to: $M$ is isomorphic to a direct sum of copies of the ring $R$. Every submodule $L$ of such a module is a summand; i.e., $$M=L\oplus N,$$ for some other submodule $N$ of $M$.
Of course, ${\bf Z}^n$ is free and finitely generated. This module is our primary interest because that's what a chain group over the integers has been every time. It behaves very similarly to ${\bf R}^n$ and the main differences lie in these two related areas. First, the quotients may have torsion, such as in ${\bf Z}/ 2{\bf Z} \cong {\bf Z}_2$. Second, some operators invertible over ${\bf R}$ may be singular over ${\bf Z}$. Take $f(x)=2x$ as an example.
We will refer to finitely generated free modules as simply modules.
The definitions
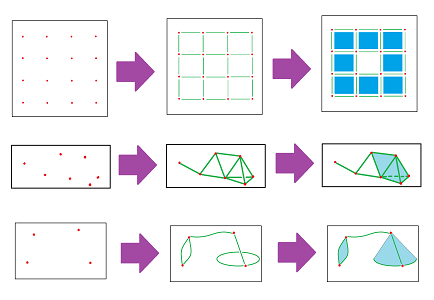
We have seen chain complexes appearing from the adjacency relation (i.e., the topology) of the cubical domain and simplicial complexes.
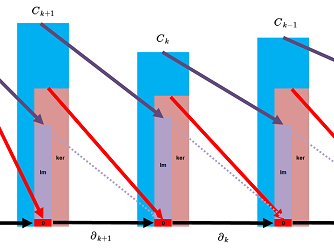
Definition. Suppose we have a sequence of modules and homomorphisms $$\partial _k : C_{k} \to C_{k-1},\ k=0,1,2, ...,$$ with zero groups (and zero homomorphisms) at the ends: $$C_{-1}=C_{N+1}=...=0.$$ The $k$th element is called the $k$-th chain group and the $k$-th boundary operator respectively. If written consecutively, they form a sequence: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} ...&\ra{}&C_{k+1}&\ra{\partial_{k+1}}&C_{k}&\ra{\partial_k}&...&\ra{\partial_1}&C_0&\ra{\partial_0=0}&0. \end{array}$$ This sequence of groups and homomorphisms is called a chain complex denoted by $$\{C_k\}:=\{C_k,\partial\}.$$ provided the composition of two consecutive boundary operators is zero: $$\partial_k\partial_{k+1}=0.$$
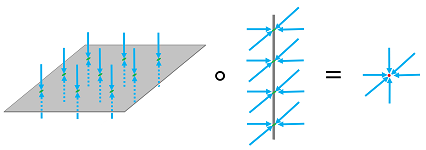
Example. As an illustration of the last condition, consider this example of two operators below. Neither operator is $0$, but their composition is:
Here,
- $A$ is the projection on the $xy$-plane, which isn't $0$;
- $B$ is the projection on the $z$-axis, which isn't $0$;
- $BA$ is $0$. $\square$
Example. A trivial chain complex: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} ...&\ra{0}&C_{k+1}&\ra{0}&C_{k}&\ra{0}&...&\ra{0}&C_0&\ra{0}&0; \end{array}$$ a "short" chain complex: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} ...&\ra{0}&C_{k+1}&\ra{}&C_{k}&\ra{0}&...&\ra{0}&C_0&\ra{0}&0; \end{array}$$ not a chain complex: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} ...&\ra{}&C_{k+1}&\ra{Id}&C_{k}&\ra{Id}&...&\ra{Id}&C_0&\ra{0}&0, \end{array}$$ unless $C_i=0$. $\square$
Definition. For a given $k=0,1,2,3,...$,
- the $k$th cycle group of $\{C_k\}$ is the subgroup of $C_k$ defined to be
$$Z_k:=\ker \partial_k;$$
- the $k$th boundary group of $\{C_k\}$ is the subgroup of $C_k$ defined to be
$$B_k:=\operatorname{Im} \partial_{k+1}.$$
Proposition. Every boundary is a cycle; i.e., for any chain complex $\{C_k\}$, $$B_k\subset Z_k,\ \forall k=0,1,2, ...$$
Proposition. For a finitely generated chain complex, the modules $C_k,Z_k,B_k$ are direct sums of finitely many copies of $R$: $$R \oplus R \oplus ... \oplus R .$$
Exercise. Prove the proposition.
Cubical complexes
We would like to be able to study functions defined on subsets of the Euclidean space.
Suppose the Euclidean space ${\bf R}^N$ is given and so is its cubical grid ${\bf Z}^N$. Suppose also that we have its decomposition ${\mathbb R}^N$, a list of all (closed) cubical cells in our grid.
Notation:
- ${\mathbb R}^N$ is the set of all cells (of all dimensions) in the grid,
- $C_k(L)$ is the set of all $k$-chains in a given collection $L\subset {\mathbb R}^N$ of cells, and, in particular,
- $C_k:=C_k({\mathbb R}^N)$ is the set of all $k$-chains in ${\mathbb R}^N$.
Proposition. The chain groups $C_k(L),\ k=0,1,2, ...$, are subgroups of $C_k=C_k({\mathbb R}^N)$.
Moreover, the chain complex comprised of these groups can be constructed in the identical way as the one for the whole ${\mathbb R}^N$ -- if we can make sense of how the boundary operators is defined: $$\partial ^L _{k}:C_{k}(L)\to C_{k-1}(L),\ \forall k=1,2,3, ....$$
One way to build them is to recognize that these are the same cells and they have the same boundaries, so we have: $$\partial ^L _{k} :=\partial _k\Big|_{C_{k}(L)}.$$ To make sure that these are well-defined, we need the boundaries of the chains in $C_k(L)$ to be chains in $C_{k-1}(L)$: $$\partial_k(C_k(L)) \subset C_{k-1}(L).$$
Definition. A cubical complex is a collection of cubical cells $K\subset {\mathbb R}^N$ that includes all faces of the cells it contains.
$N=2:$
$N=3:$
Example. The cubical complex $K$ of the pixel at the origin is given by a list of cells of all dimensions:
- 0. $\{0 \} \times \{0 \},\ \{1 \} \times \{0 \},\ \{0 \} \times \{1 \}, \{1 \} \times \{1 \}$;
- 1. $\{0 \} \times [0,1],\ [0,1] \times \{0 \},\ [0,1] \times \{1 \},\ \{1 \} \times [0,1]$;
- 2. $[0,1] \times [0,1]$. $\\$
Now, their boundaries are defined within the complex:
- 0. $\partial \Big( \{(0, 0) \} \Big) = 0$, etc.,
- 1. $\partial \Big( \{0 \} \times [0,1] \Big) = \{(0,0) \} + \{(0,1) \}$, etc.,
- 2. $\partial \Big( [0,1] \times [0,1]\Big) = [0,1] \times \{0 \} + \{0 \} \times [0,1] + [0,1] \times \{1 \} + \{1 \} \times [0,1]$. $\square$
Proposition. The boundary operator on a cubical complex is well-defined.
Proposition. The chain groups and the boundary operators of a cubical complex form a chain complex: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} ...& \ra{\partial_{k+2}} & C_{k+1}(K)& \ra{\partial_{k+1}} & C_{k}(K)& \ra{\partial_{k}} & C_{k-1}(K) & \ra{\partial_{k-1}} & ... & \ra{\partial_1} & C_1(K)& \ra{\partial_0} & 0. \end{array} $$
Definition. The dimension $\dim K$ of a cubical complex $K$ is the highest among the dimensions of its cells.
Just keep in mind that the shared vertices, edges, faces, etc. appear only once.
Exercise. Find the cubical complex representation of the regular, hollow, torus.
The rest of the definitions apply.
Definition. For a given $k=0,1,2,3,...$,
- the $k$th cycle group of $K$ is the subgroup of $C_k=C_k(K)$ defined to be
$$Z_k=Z_k(K):=\ker \partial_k;$$
- the $k$th boundary group of $K$ is the subgroup of $C_k(K)$ defined to be
$$B_k=B_k(K):=\operatorname{Im} \partial_{k+1}.$$
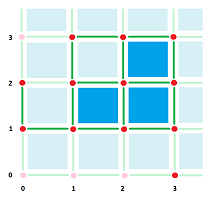
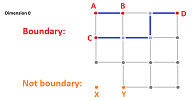
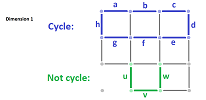
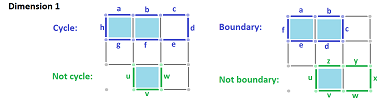
This is how cycles and boundaries are visualized.
Example. We choose to have only $0$- and $1$-cells. This is how we visualize boundaries and cycles, in the only two relevant dimensions:
$\square$
Exercise. Use the example above to show that the cycles and boundaries with respect to a cubical complex are different from those with respect to ${\mathbb R}^N$.
Exercise. For the complexes shown in this subsection, sketch a few examples of cycles and boundaries.
Examples of chain complexes of cubical complexes
Over $R={\bf Z}_2$, all these groups are just lists. Indeed, $C_k(K)$ is generated by the finite set of $k$-cells in $K$ and $Z_k(K),B_k(K)$ are its subgroups. Therefore, they all have only finite number of elements.
We will start with these three, progressing from the simplest to more complex, in order to reuse our computations:
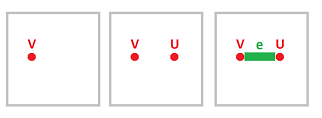
Example (single vertex). Let $K:=\{V\}$. Then $$\begin{array}{llll} C_0&=< V > &=\{0,V\},\\ C_i& &=0, &\forall i>0. \end{array}$$ Then we have the whole chain complex here: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} 0 & \ra{\partial_2=0} & C_1=0& \ra{\partial_1=0} & C_0 =< V > & \ra{\partial_0=0} & 0. \end{array} $$ From this complex, working algebraically, we deduce: $$\begin{array}{lllllll} Z_0:=&\ker \partial _0 &= < V > &=\{0,V\},\\ B_0:=&\operatorname{Im} \partial _1 & &=0. \end{array}$$ $\square$
Example (two vertices). Let $K:=\{V, U\}$. We copy the last example and make small corrections: $$\begin{array}{llllll} C_0&=< V,U > &=\{0,V,U,V+U\},\\ C_i& &=0, &\forall i>0. \end{array}$$ Then we have the whole chain complex here: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} 0 & \ra{\partial_2=0} & C_1=0 & \ra{\partial_1=0} & C_0 =< V,U > & \ra{\partial_0=0} & 0. \end{array} $$ Now using only algebra, we deduce: $$\begin{array}{llllll} Z_0:=&\ker \partial _0 &= < V,U > &=\{0,V,U,V+U\},\\ B_0:=&\operatorname{Im} \partial _1 & &=0. \end{array}$$ $\square$
Example (two vertices and an edge). Let $K:=\{V, U, e\}$. We copy the last example and make some corrections: $$\begin{array}{llllll} C_0&=< V,U >&=\{0,V,U,V+U\},\\ C_1&=< e >&=\{0,e\},\\ C_i&=0, &\forall i>1. \end{array}$$ Then we have the whole chain complex shown: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} 0 & \ra{\partial_2=0} & C_1=< e >& \ra{\partial_1=?} & C_0 =< V,U > & \ra{\partial_0=0} & 0. \end{array} $$ First we compute the boundary operator: $$\partial _1 (e)=V+U.$$ Hence, $$\partial _1 =[1,1]^T.$$ Now the groups.
Dimension $0$ (no change in the first line): $$\begin{array}{llllll} Z_0:=&\ker \partial _0 &= < V,U >&=\{0,V,U,V+U\},\\ B_0:=&\operatorname{Im} \partial _1 &=< V+U >&=\{0,V+U\}. \end{array}$$ Notice the inexactness of our chain complex: $Z_0 \ne B_0$ (not every cycle is a boundary!).
Dimension $1$: $$\begin{array}{llllll} Z_1:=&\ker \partial _1 &= 0,\\ B_1:=&\operatorname{Im} \partial _2 &=0. \end{array}$$ $\square$
Two, slightly more complex, examples:
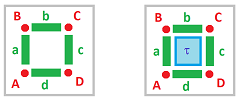
Example (hollow square). Let $K:=\{A, B,C,D, a,b,c,d\}$. Then we have (too many cells to list all elements): $$\begin{array}{llllll} C_0&=< A,B,C,D >,\\ C_1&=< a,b,c,d >,\\ C_i&=0, \quad\forall i>1. \end{array}$$ Note that we can think of these two lists of generators as ordered bases.
We have the chain complex below: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} 0 & \ra{\partial_2=0} & C_1=< a,b,c,d > & \ra{\partial_1=?} & C_0 =< A,B,C,D > & \ra{\partial_0=0} & 0. \end{array} $$ First we compute the boundary operator: $$\begin{array}{llllll} \partial _1 (a)&=A+B,\\ \partial _1 (b)&=B+C,\\ \partial _1 (c)&=C+D,\\ \partial _1 (d)&=D+A. \end{array}$$ Hence, $$\partial _1 =\left[ \begin{array}{ccccccccccccc} 1,&0,&0,&1\\ 1,&1,&0,&0\\ 0,&1,&1,&0\\ 0,&0,&1,&1 \end{array} \right].$$ The chain complex has been found, now the groups.
Dimension $0$: $$\begin{array}{llllll} Z_0:=&C_0 & &= < A,B,C,D >,\\ B_0:=&\operatorname{Im} \partial _1 &=< A+B,B+C,C+D,D+A > &=< A+B,B+C,C+D > \end{array}$$ (because $D+A$ is the sum of the rest of them).
Dimension $1$: $$\begin{array}{llllll} Z_1:=&\ker \partial _1 &= ?,\\ B_1:=&\operatorname{Im} \partial _1 &=0. \end{array}$$ To find the kernel, we need to find all $e=(x,y,z,u)\in C_1$ such that $\partial _1 e=0$. That's a (homogeneous) system of linear equations: $$\left\{ \begin{array}{ccccccccccccc} x & & &+u &=0,\\ x &+y & & &=0,\\ & y & +z& &=0,\\ & & z &+u &=0. \end{array} \right .$$ Solving from bottom to the top: $$z=-u \Longrightarrow y=u \Longrightarrow x=-u,$$ so $e=(-u,u,u,-u)^T,\ u\in {\bf R}$. Then, as signs don't matter, $$Z_1=< e >=<(1,1,1,1)>=<a+b+c+d>.$$ $\square$
Example (solid square). Let $K:=\{A, B,C,D, a,b,c,d, \tau \}$. We copy the last example and make some corrections. We have: $$\begin{array}{llllll} C_0&=< A,B,C,D >,\\ C_1&=< a,b,c,d >,\\ C_2&=<\tau>,\\ C_i&=0, \quad\forall i>2. \end{array}$$ We have the chain complex: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} 0 & \ra{\partial_3=0} & C_2=<\tau >&\ra{\partial_2=?} & C_1=< a,b,c,d > & \ra{\partial_1} & C_0 =< A,B,C,D >& \ra{\partial_0=0} & 0. \end{array} $$ First we compute the boundary operator: $$\partial _2 (\tau)=a+b+c+d,$$ therefore, $$\partial _2 =[1,1,1,1]^T.$$ As $\partial _1$ is already known, the chain complex has been found. Now the groups:
Dimension $0$. Since the changes in the chain complex don't affect these groups, we have answers ready: $$\begin{array}{llllll} Z_0:=&C_0 &= < A,B,C,D >,\\ B_0:=&\operatorname{Im} \partial _1 &=< A+B,B+C,C+D >.\\ \end{array}$$
Dimension $1$ (no change in the first line): $$\begin{array}{llllll} Z_1:=&\ker \partial _1 & &= <a+b+c+d>,\\ B_1:=&\operatorname{Im} \partial _1 &=< \partial _2(\tau) > &=<a+b+c+d>. \end{array}$$ $\square$
Exercise. Represent the sets below as realizations of cubical complexes. In order to demonstrate that you understand the algebra, for each of them:
- (a) find the chain groups and find the boundary operator as a matrix;
- (b) using only part (a) and algebra, find $Z_k,B_k$ for all $k$, including the generators.
Exercise. Compute the chain complex of a “train” with $n$ cars:
Cubical and simplicial domains
Can we have a discrete representation of a punctured plane, etc? Unfortunately, removing a vertex from ${\mathbb R}^N$ leave us with a collection of cells that is not a cubical complex. Are there other subsets of chains that form chain complexes? Yes, the complements of the cubical complexes.
Definition. A cubical domain $K$ is a set of cells $K\subset {\mathbb R}^N$ that is a cubical complex or the complement of a cubical complex.
Considering that in the latter case some boundary faces are missing, is the boundary operator well defined?
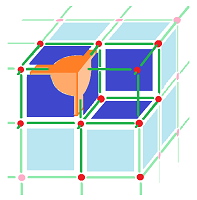
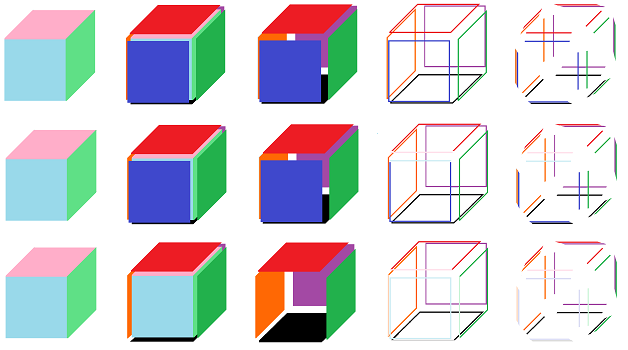
Example. Below we start with the complex $K$ of the cube in the left-most column. We then remove a three simple subcomplexes from this complex and visualize the boundary of the boundary of the $3$-cell $Q$, i.e., $\partial\partial Q$, in the left-most column.
When a vertex is removed, there is no difference. When an edge -- with its end-points -- is removed, it does not appear in $\partial\partial Q$ while the rest of the edges are paired up and cancel. Finally, when face -- with its boundary edges -- is removed, these four edges don't appear in $\partial\partial Q$, while the rest are still paired up. $\square$
The idea is explained algebraically as follows.
Suppose $K$ is a cubical complex in ${\mathbb R}^N$ and $U$ is its complement: $$U:={\mathbb R}^N \setminus K.$$ Then $$C_k({\mathbb R}^N)=C_k(K)\oplus C_k(U).$$ Therefore, the projection $$p_k:C_k({\mathbb R}^N) \to C_k(U)$$ is well-defined.
Definition. We define the boundary operator on the cubical domain $U$ $$\partial_k^U:C_k(U)\to C_{k-1}(U),\ k=0,1,...$$ by $$\partial_k^U :=p_k \partial_k.$$
Proposition. The boundary operator on a cubical domain is well-defined.
Proposition. The chain groups and the boundary operators of a cubical domain form a chain complex.
Exercise. Prove the proposition. Hint: $C(U) \cong C / C(K)$.
We have a similar development for the simplicial case.
Definition. A simplicial domain $K$ is a subset of of a simplicial complex $M$ that is a simplicial complex or the complement of a simplicial complex.
Suppose $K$ is a subcomplex of a simplicial complex $M$ and $U$ is its complement: $$U:=M \setminus K.$$ Then $$C_k(M)=C_k(K)\oplus C_k(U).$$ Therefore, the projection $$p_k:C_k(M) \to C_k(U)$$ is well-defined.
Definition. We define the boundary operator on the simplicial domain $U$ $$\partial_k^U:C_k(U)\to C_{k-1}(U),\ k=0,1,...$$ by $$\partial_k^U :=p_k \partial_k.$$
Proposition. The boundary operator on a simplicial domain is well-defined.
Proposition. The chain groups and the boundary operators of a simplicial domain form a chain complex.
The rest of the definitions apply: cycles and boundaries.
Examples of chain complexes
We are already familiar with gradual and orderly building -- via skeleta -- of cubical and simplicial complexes:
The only difference is that now we have more flexibility about the cells. We will assume that they are balls of various dimensions:
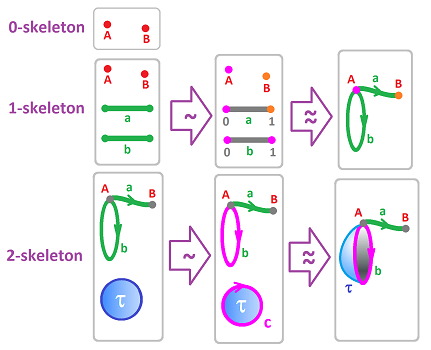
Example (ladle). Let's consider a specific example. Suppose we want to build something that looks like a ladle, which is the same topologically as a Ping-Pong bat:
We want to build a simple topological space from the ground up, using nothing but cells attached to each other in the order of increasing dimensions. In our box, we have: the parts, the glue, the schematics, and a set of instructions of how to build it.
Here is the schematics:
Let's narrate the instructions. We start with the list $K$ of all cells arranged according to their dimensions:
- dimension $0$: $A,B$;
- dimension $1$: $a,b$;
- dimension $2$: $\tau$. $\\$
These are the building blocks. At this point, they may be arranged in a number of ways.
Now, the two points $A,B$ are united into one set. That's the $0$-skeleton $K^{(0)}$ of $K$.
Next, we take this space $K^{(0)}$ and combine it, again as the disjoint union, with all $1$-cells in $K$. To put them together, we introduce an equivalence relation on this set. But, to keep this process orderly, we limit ourselves to an equivalence relation between the vertices (i.e., the elements of $K^{(0)}$) only, and the boundaries of the $1$-cells we are adding. In other words, we identify the endpoints of $a$ and $b$ to the points $A$ and $B$. This can happen in several ways. We make our choice by specifying the attaching map for each $1$-cell thought of as a segment $[0,1]$: $$f_a:\partial a\to K^{(0)},\ f_b:b\to K^{(0)} ,$$ by specifying the values on the endpoints: $$f_a(0)=A,\ f_a(1)=B,\ f_b(0)=A,\ f_b(1)=A.$$ We use these maps following the attaching rule: $$x\sim y \Longleftrightarrow f_a(x)=y.$$ The result is the $1$-skeleton $K^{(1)}$.
The rule we have followed is to choose
Next, we take this space $K^{(1)}$ and combine it, again as the disjoint union, with all $2$-cells in $K$. To put them together, we introduce an equivalence relation following the rule above. For this dimension, we identify the edge of $\tau$ with a $1$-cell $a$, point by point. This can happen in several ways and we make our choice by specifying the attaching map for the $2$-cell: $$f_{\tau}:\tau\to K^{(1)} .$$ We only need to specify the values on the boundary and we assume that $f_{\tau}:\partial\tau\to b$ is a bijection. We again use the attaching rule: $$x\sim y \Longleftrightarrow f_{\tau}(x)=y.$$ The result is the $2$-skeleton $K^{(2)}$, which happens to be the whole $K$. $\square$
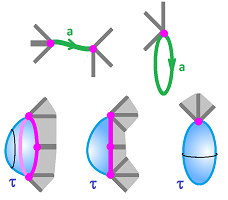
A $1$-cell may be attached to $0$-cells as a rope or as a noose:
Meanwhile, a $2$-cell may be attached to $1$-cells as a soap film, a zip-lock bag, or an air-balloon.
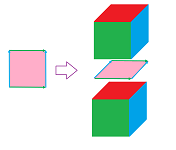
We proceed to algebra. If the (topological) boundary of an $(n+1)$-cell $\tau$ is the union of several $n$-cells $a, b, c, ...$: $$\partial \tau = a \cup b \cup c \cup ...,$$ then the boundary operator evaluated at $\tau$ is some linear combination of these cells: $$\partial _{n+1}(\tau) = \pm a\pm b\pm c\pm...$$
What are the signs? They are determined by the orientation of the cell $\tau$ as it is attached to $n$-cells. Let's consider this matching in lower dimensions.
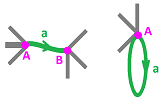
In dimension $1$, the meaning of orientation is simple. It is the direction of the $1$-cell as we think of it as a parametric curve. Then the boundary is the last vertex it is attached to minus the first vertex.
Here, if the (topological) boundary of the $1$-cell $a$ is identified, by the attaching maps, with the union of two $0$-cells $A, B$ (or just $A$), while the (algebraic) boundary of $a$ is the sum (or a linear combination) of $A, B$: $$\begin{array}{lllllll} f_a(\partial a) &= \{A,B\} &\leadsto &\partial _1 (a) = B-A;\\ f_a(\partial a) &= \{A\} &\leadsto &\partial _1 (a) = A-A=0. \end{array}$$
For a $2$-cell, a direction is chosen for its circular boundary, clockwise or counterclockwise. As we move along the boundary following this arrow, we match the direction to that of each $1$-cell we encounter:
Here, we have three cases: $$\begin{array}{lllllll} f_{\tau}(\partial \tau) &= a \cup b \cup c &\leadsto& \partial _2\tau &= a - b - c;\\ f_{\tau}(\partial \tau) &= a \cup b &\leadsto& \partial _2\tau &= -a - b +a+b=0;\\ f_{\tau}(\partial \tau) &= A &\leadsto & \partial _2\tau &= 0. \end{array}$$
Initially, we can understand the orientation of a cell as an ordering of its vertices, just as we did for simplicial complexes.
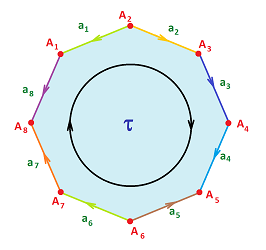
Example. Let's evaluate the boundary operator for this $2$-cell, with the orientations of $1$-cells randomly assigned.
We have: $$\partial \tau = -a_1 + a_2 + a_3 + a_4 - a_5 + a_6 + a_7 - a_8.$$ Further, $$\begin{array}{llll} \partial (\partial \tau) &=& \partial( -a_1 + a_2 + a_3 + a_4 - a_5 + a_6 + a_7 - a_8 ) \\ &=& -\partial a_1 + \partial a_2 + \partial a_3 + \partial a_4 - \partial a_5 + \partial a_6 + \partial a_7 - \partial a_8 \\ &=& -(A_1 - A_2) + (A_3 - A_2) + (A_4 - A_3) + (A_5 - A_4) \\ && - (A_5 - A_6) + (A_7 - A_6) + (A_8 - A_7) - (A_8 - A_1) \\ &=& 0. \end{array}$$$\square$
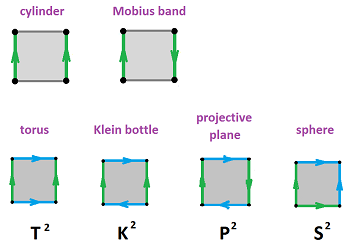
This is what we can construct from the square by gluing one or two pairs of its opposite edges:
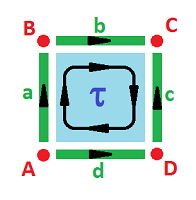
Example (square). Here is the simplest cell representation of the square (even though the orientations can be arbitrarily reversed):
The complex $K$ of the square is:
- $0$-cells: $A, B, C, D$;
- $1$-cells: $a, b, c, d$;
- $2$-cells: $\tau$;
- boundary operator: $\partial \tau = a + b + c - d; \ \partial a = B-A, \partial b = C-B$, etc. $\square$
Example (cylinder). We can construct the cylinder $C$ by gluing two opposite edges with the following equivalence relation: $(0,y) \sim (1,y)$. The result of this equivalence relation of points can be seen as equivalence of cells: $$a \sim c;\ A \sim D,\ B \sim C.$$
We still have our collection of cells (with some of them identified as before) and only the boundary operator is different:
- $\partial \tau = a + b + (-a) - d = b - d ;$
- $\partial a = B-A,\ \partial b = B-B=0,\ \partial d = A-A = 0.$ $\\$
The chain complex is $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_2 & \ra{\partial} & C_1 & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b,d > & \ra{?} & < A,B > \\ & & \tau & \mapsto & b - d \\ & & & & a & \mapsto & B-A \\ & & & & b & \mapsto & 0 \\ & & & & d & \mapsto & 0 \\ {\rm kernels:} & & Z_2 = 0 && Z_1 = < b,d > & & Z_0 = < A,B > \\ {\rm images:} & & B_2 = 0 && B_1 = < b - d > & & B_0 = < B-A > \end{array}$$ Here, “kernels” are the kernels of the maps to their right, “images” are the images of the maps to their left. $\square$
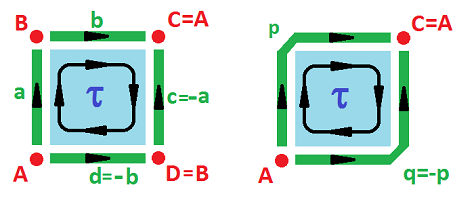
Example (Möbius band). In order to build the Möbius band ${\bf M}^2$, we use the equivalence relation: $(0,y) \sim (1,1-y)$. Once again, we can interpret the gluing as equivalence of cells, $a$ and $c$. But this time they are attached to each other with $c$ upside down. It makes sense then to interpret this as equivalence of cells but with a flip of the sign: $$c \sim -a.$$ Here $-c$ represents edge $c$ with the opposite orientation:
In other words, this is an equivalence of chains. Further, $$A \sim D, \ B \sim C.$$ The boundary operator is:
- $\partial \tau = a + b - (-a) - d = 2a + b - d;$
- $\partial a = B-A, \ \partial b = A-B, \ \partial d = B-A.$ $\\$
The chain complex is $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_2 & \ra{\partial} & C_1 & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b,d > & \ra{?} & < A,B > \\ & & \tau & \mapsto & 2a + b - d \\ & & & & a & \mapsto & B-A \\ & & & & b & \mapsto & A-B \\ & & & & d & \mapsto & B-A \\ {\rm kernels:} & & Z_2 = 0 && Z_1 = < a+b,a-d > & & Z_0 = < A,B > \\ {\rm images:} & & B_2 = 0 && B_1 = < 2a+b-d > & & B_0 = < B-A > \end{array}$$ $\square$
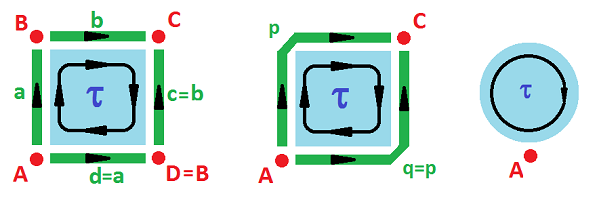
Example (sphere). We can either build the sphere as a quotient of the square or, easier, we just combine these pairs of the consecutive edges:
Then we have only two edges left. Even better, the last option gives us a representation with no $1$-cells whatsoever! $\square$
Example (projective plane). The projective plane comes from a certain quotient of the disk, ${\bf B}^2/_{\sim}$, where $u \sim -u$ is limited to the boundary of the disk. It can also be seen as a quotient of the square:
As we see, the edge of the disk is glued to itself, with a twist. Its algebraic representation is almost the same as before: $p\sim -p$.
- $2$-cells: $\tau$ with $\partial\tau = 2p$;
- $1$-cells: $p$ with $\partial p = 0$;
- $0$-cells: $A$ with $\partial A = 0$.
$\square$
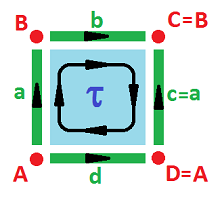
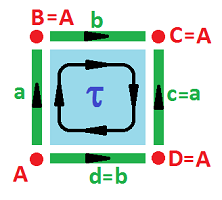
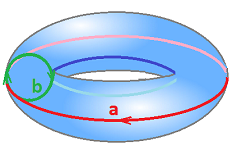
Example (torus). What if after creating the cylinder by identifying $a$ and $c$ we then identify $b$ and $d$? Like this: $$c \sim a,\ d \sim -b.$$ The result is the torus ${\bf T}^2$:
Note how all the corners of the square come together in one. Then the chain complex has very few cells to deal with: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_2 & \ra{\partial} & C_1 & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b > & \ra{?} & < A > \\ & & \tau & \mapsto & 0 \\ & & & & a & \mapsto & 0 \\ & & & & b & \mapsto & 0 \\ {\rm kernels:} & & Z_2 = < \tau > && Z_1 = < a,b > & & Z_0 = < A > \\ {\rm images:} & & B_2 = 0 && B_1 = 0 & & B_0 = 0 \end{array}$$
$\square$
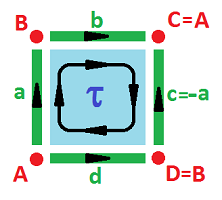
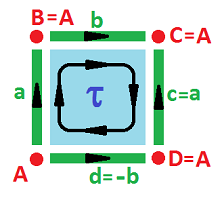
Example (Klein bottle). What if we flip one of the edges before gluing? Like this: $$c \sim a,\ d \sim -b.$$
The corners once again come together in one and the chain complex has very few cells to deal with: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_2 & \ra{\partial} & C_1 & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b > & \ra{?} & < A > \\ & & \tau & \mapsto & 2a \\ & & & & a & \mapsto & 0 \\ & & & & b & \mapsto & 0 \\ {\rm kernels:} & & Z_2 = 0 && Z_1 = < a,b > & & Z_0 = < A > \\ {\rm images:} & & B_2 = 0 && B_1 = < 2a > & & B_0 = 0 \end{array}$$ $\square$
This is how we can build in dimension $3$. We start with a cube. First, we glue its top and bottom, with each point identified to the one directly underneath. Then we cut the cube into two by a horizontal square.
Exercise. Consider the relations listed above to identify the edges of this square, just as we did for the torus, etc. Use these relations to glue the opposite faces of the cube and compute the resulting chain complex.
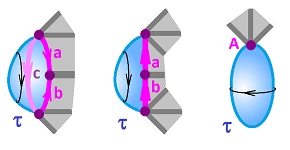
Example (balls). We represent ${\bf B}^n$: Cells:
- $n$-cells: ${\sigma}$,
- $(n-1)$-cells: $a$,
- $0$-cells: $A$. $\\$
The boundary operator:
- ${\partial}{\sigma} = a,$
- ${\partial}a = 0,$
- ${\partial}A = 0.$
The chain complex is below: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccccccccccccc} & C_n & \ra{\partial} & C_{n-1} & \ra{\partial} & C_{n-2} & \to ... \to & C_0 \\ & < \sigma > & \ra{\cong} & < a > & \ra{0} & 0 & \to ... \to & < A > \\ & {\sigma} & \mapsto & a & \mapsto & 0 & & A & \\ {\rm kernels:} & Z_n = 0 & & Z_{n-1} = < a > & & Z_{n-2} = 0 & ... & Z_0 = < A > \\ {\rm images:} & B_n = 0 & & B_{n-1} = < a > & & B_{n-2} = 0 & ... & B_0 = 0 &\square \end{array}$$
Example (spheres). The sphere ${\bf S}^{n-1}$ has the same representation as the ball except the $n$-cell is missing: The cells:
- $(n-1)$-cells: $a$,
- $0$-cells: $A$. $\\$
The boundary operator:
- ${\partial}a = 0,$
- ${\partial}A = 0.$
The chain complex is: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccccccc} & C_n & \ra{\partial} & C_{n-1} & \ra{\partial} & C_{n-2} & \to ... \to & C_0 \\ & 0 & \ra{0} & < a > & \ra{0} & 0 & \to ... \to & < A > & \\ & & & a & \mapsto & 0 & & A & \\ {\rm kernels:} & Z_n = 0 & & Z_{n-1} = < a > & & Z_{n-2} = 0 & ... & Z_0 = < A > \\ {\rm images:} & B_n = 0 & & B_{n-1} = 0 & & B_{n-2} = 0 & ... & B_0 = 0 &\quad\square \end{array}$$