Calculus on graphs

The algebra of plumbing, continued

We introduce more algebra with the familiar metaphor.

We think of a graph as a plumbing system that consists of a network of pipes and joints, and each joint and each pipe is equipped with an on-off switch.

The two plumbers “flip the switch” on a joint or a pipe which is recorded with binary numbers and the repeated flips are cancelled via binary addition. Since this activity is happening at every joint and every pipe, we have the two groups: the chains of nodes and the chains of edges: $$C_0\cong ({\bf Z}_2)^n,\ C_1\cong ({\bf Z}_2)^m.$$

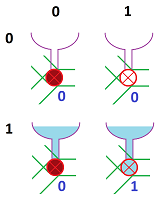
Let's concentrate on a single switch. We assume that it is closed in the beginning of the day. Then the combined request will tell us the state of each switch in the end of the day. We use $0$ for closed and $1$ for open.

We add water now.

Behind the switch is a reservoir. We look at:

• the state of the reservoir (full or empty),
• the request for the switch, and
• the resulting flow of water.

All of these are binary numbers, $0$ or $1$. How this works is obvious:

• pump on ($1$) and switch flipped ($1$), then water flows ($1$);
• pump off ($0$) and switch flipped ($1$), then water doesn't flow ($0$); etc. $\\$

We discover that this isn't binary addition but binary multiplication: $$1\times 1=1,\ 0\times 1=0,\ 1\times 0 =0,\ 0\times 0=0.$$

It is important that the two numbers in the left-hand side refer to two very different entities and it would be misleading to suggest that these are group operations. Instead, let's rename the states of the reservoir as $0^*$ and $1^*$. Then we have: $$1^*\times 1=1,\ 0^*\times 1=0,\ 1^*\times 0 =0,\ 0^*\times 0=0.$$ In fact, the best way to think of these two numbers is as functions: $$1^*(1)=1,\ 0^*(1)=0,\ 1^*(0) =0,\ 0^*(0)=0.$$ Furthermore, the distributive property proves that these are homomorphisms $$x^*:{\bf Z}_2 \to {\bf Z}_2.$$ These simple functions, $0^*$ and $1^*$, are defined for every switch and, therefore, for all chains; these functions are called cochains.

The dual of a group

What follows is the algebra we need in order to understand these binary cochains.

Given a group $L$, its dual $L^*$ (over ${\bf Z}_2$) is the set of all homomorphisms on $L$, $$s:L \to {\bf Z}_2.$$

Let's start with this simplest group: $$L=\{0,A\} \cong {\bf Z}_2,$$ with $A+A=0$, etc. There are only two such homomorphisms: the zero and the identity. The former may be thought of as the multiplication by $0$ and the latter by $1$. We can denote them by $0^*$ and $1^*$, just as in the last subsection. Then, $$L^*:=\{0^*,1^*\}.$$ In other words, we see the following again: $$0^*(0)=0,\ 0^*(1)=0,\ 1^*(0)=0,\ 1^*(0)=1.$$

A more general case is: $$L:= \underbrace{{\bf Z}_2\oplus{\bf Z}_2\oplus ... \oplus {\bf Z}_2}_\text{n times}=\Big( {\bf Z}_2 \Big)^n .$$ Every element of $L$ is written as $$x=(x_1,...,x_n), \ x_i\in{\bf Z}_2.$$ Then every element of $L^*$ is written as $$x=(x_1^*,...,x_n^*), \ x_i\in{\bf Z}_2.$$ Therefore, $$L^* \cong \Big( {\bf Z}_2 \Big)^n .$$

Since the sum of two homomorphisms is a homomorphism, we make the following conclusion.

Proposition. The dual of ${\bf Z}_2$ is a group isomorphic to ${\bf Z}_2$.

So, $L\cong L^*$! However, this doesn't mean that those two are the same thing.

The first crucial difference is that we can multiply the elements of the latter, because the product of two homomorphisms to a given group is also a homomorphism. We make the following conclusion.

Proposition. The dual $L^*$ is a ring.

Exercise. Prove the proposition.

Exercise. Define and find the dual over ${\bf Z}_2$ of the group ${\bf Z}_3$.

Further, what happens to the dual $L^*$ under homomorphisms of $L$?

As it turns out, this is a wrong question to ask. Suppose there is another group $K$ and suppose $h:L\to K$ is a homomorphism. Then, for any $s\in L^*$, what happens is seen in the following diagrams: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccccccccc} L &\ra{s} & {\bf Z}_2 &\quad & A\ \ & \mapsto & 0\text { or } 1\\ \ \ \da{h} & & || &\quad & \da{h} & & ||\ ? \\ K &\ra{t} & {\bf Z}_2 &\quad & h(A) & \mapsto & 0\text { or } 1 \end{array}$$ It would be natural to try to express the “new” function $t$ in terms of the “old” $s$, but it's impossible to combine $s$ with $h$. In fact, it is the opposite that we need to consider -- $th$ makes sense and $ht$ doesn't. Then we simply require the first diagram to be commutative or, which is the same thing, that the outputs of the two homomorphisms coincide on the right in the second diagram. As a result, $s$ is defined in terms of $t$: $$s(A):=th(A).$$ Then $t\in K^*$ is the input and $s\in L^*$ is the output of the new homomorphism.

To summarize, the dual homomorphism of a homomorphism $$h:L\to K$$ is the homomorphism (note the direction of the arrow) $$h^*:K^*\to L^*,$$ defined by the identity: $$h(y^*)(x):=y^*h(x),$$ for any $x\in L$ and any $y\in K$.

Exercise. For $L$ and $K$ chosen to be either ${\bf Z}_2$ or ${\bf Z}_2\oplus {\bf Z}_2$, provide a formula for $h^*$ for every possible $h$.

Exercise. How many homomorphisms $({\bf Z}_2)^n\to {\bf Z}_2$ are there?

Cochains of nodes and cochains of edges

We apply the algebra developed in the last subsection to cochains.

Suppose we are given a graph $G$ with the set of nodes $N$ and the set of edges $E $. Then the group of chains of nodes, or $0$-chains, and the group of chains of edges, or $1$-chains, are respectively: $$\begin{array}{lllll} C_0=C_0(G)&:=\Big\{\displaystyle\sum_{A\in Q} A: A \subset N\Big\} \cup \{0\} &=< N >,\\ C_1=C_1(G)&:=\Big\{\displaystyle\sum_{AB\in P} AB: P \subset E\Big\} \cup \{0\}&=< E >. \end{array}$$

Definition. A $k$-cochain on graph $G$ is a homomorphism $s:C_k(G) \to {\bf Z}_2$.

Since the sum of two homomorphisms is a homomorphism, we make the following conclusion.

Proposition. The $0$- and $1$-cochains on graph $G$ form groups, denoted by $C^0(G)$ and $C^1(G)$ respectively (not to be confused with the set of differentiable functions).

If we consider one node (or edge) at a time, we are in the setting of the last subsection. As we know, there are only two such homomorphisms: the zero $0^*$ and the identity $1^*$. Therefore,

• a $0$-cochain assigns a number, $0$ or $1$, to each node, and
• a $1$-cochain assigns a number, $0$ or $1$, to each edge. $\\$

Just like chains!

There is a special way to present the cochains in terms of the “basic chains”, i.e., the nodes and the edges. For every such chain $x\in C_k,\ k=0,1$, define a “basic cochain” $x^*:C_k\to {\bf Z}_2$, by $$x^*(t):=\begin{cases} 1 & \text{ if } t=x,\\ 0 & \text{ if } t\ne x. \end{cases}$$ Then every cochain is simply the sum of a set of the basic cochains.

Proposition. $$\begin{array}{lll} C^0&:=\Big\{\displaystyle\sum_{A^*\in Q} A: A \subset N\Big\} \cup \{0\} &\cong {\bf Z}_2,\\ C^1&:=\Big\{\displaystyle\sum_{AB^*\in P} AB: P \subset E\Big\} \cup \{0\}&\cong{\bf Z}_2. \end{array}$$

Proposition. The function $x\mapsto x^*$ generates an isomorphism between the groups of chains and cochains: $$C_k\cong C^k.$$

Since everything is expressed in terms of these generators, this isomorphism is given explicitly by $$\Big( \sum_i A_i \Big)^*:=\sum_i A_i^*.$$

Exercise. Prove the propositions.

Next, with ordered sets of nodes $N$ and edges $E$ fixed as bases of the groups of chains, both chains and cochains can be written coordinate-wise, as column-vectors and row-vectors.

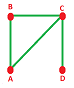
Example. Let's once again consider this graph $G$:

• $N=\{A,B,C,D\}$,
• $E=\{AB,BC,CA,CD\}$.

Then its chains of nodes are $$A=\left[ \begin{array}{llllll} 1 \\ 0 \\ 0\\ 0 \end{array} \right],\ B=\left[ \begin{array}{lllll} 0 \\ 1 \\ 0\\ 0 \end{array} \right],\ ...,\ A+B=\left[ \begin{array}{lllll} 1 \\ 1 \\ 0\\ 0 \end{array} \right],\ ... $$ Then the cochains of nodes are: $$A^*=[1,0,0,0],\ B^*=[0,1,0,0],\ ...,\ (A+B)^*=[1,1,0,0],\ ...$$ Similarly, the cochains of edges are: $$\hspace{.12in}AB^*=[1,0,0,0],\ BC^*=[0,1,0,0],\ ...,\ (AB+BC)^*=[1,1,0,0],\ ...\hspace{.12in}\square$$

Proposition. The value of a cochain $s$ at a given chain $a$ is the dot-product of the two: $$s(a)=\langle s,a \rangle.$$

We always put the cochain first in this dot product. This way, the output is simply the matrix product $sa$ of a $1\times n$ matrix $s$ and an $n\times 1$ matrix $a$.

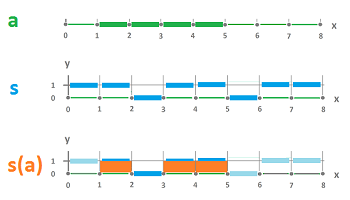
Example. To illustrate this formula, let's consider a very simple example:

• $G$, a graph with $8$ edges numbered from $0$ to $8$,
• $a$, a chain equal to the sum of the edges from $1$ to $5$, and
• $s$, a cochain with $1$s and $0$'s shown.

Then, $$a=[0,1,1,1,1,1,0,0,0]^T,\ s=[1,1,0,1,1,0,1,1].$$ We compute: $$\begin{array}{lllll} s(a)&=\langle s,a \rangle =\sum_i s_ia_i\\ &=1\cdot 0+1\cdot 1+0\cdot 1+1\cdot 1+1\cdot 1+0\cdot 0+1\cdot 0 +1\cdot 0\\ &=1\cdot 1+0\cdot 1+1\cdot 1+1\cdot 1 =1. \end{array}$$ This is the (binary) area under the graph of $s$! (One can also imagine the plumber keeping a binary count of how many times he has flipped the switch.) $\square$

The notation so justified is: $$s(a)= \displaystyle\int_a s, \quad \text{ or } s(AB)= \displaystyle\int_A^B s.$$ Meanwhile, in this context, cochains are called discrete differential forms, to be discussed later.

Exercise. Verify the counterparts of the Linearity, Additivity, and other properties of the Riemann integral.

Exercise. Provide a similar, integral interpretation of $0$-cochains.

Maps of cochains

Now, what happens to chains under graph maps is very simple. If $f:G\to J$ is such a map, its chain maps $$f_k:C_k(G)\to C_k(J)$$ are defined as follows. If $A$ is a node in $G$, then we have the following: $$f_0(A)=f(A).$$

What about the cochains? We already know that the arrows will be reversed, in a “dual” way.

Suppose $s$ is a $k$-cochain in $G$ and $t$ in $J$. Then the relation between them is seen in the following commutative diagram: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccccccccc} C_k(G)&\ra{s}& {\bf Z}_2 \\ \da{f_k}& & || \\ C_k(J)&\ra{t}& {\bf Z}_2 \end{array}$$

Definition. The $k$-cochain map, $k=0,1,...$, of a graph map $f:G\to J$ are the homomorphisms (note the direction of the arrow): $$f^k:C^k(J)\to C^k(G),$$ defined by $$f^k(t)(a):=tf_k(a),$$ for any $k$-chain $a$ in $G$ and any $k$-cochain $t$ in $J$.

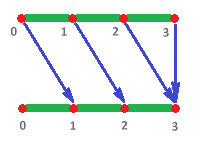
Example. Let's consider the formula for a specific $f:G\to G$, the shift (with one collapse) of the three-edge graph $G$:

• $G:=\{0,1,2,3;\ 01,12,23\}$,
• $f(0)=1,\ f(1)=2,\ f(2)=3,\ f(3)=3.$

First, the nodes. We have

• $f_0(0)=1,\ f_0(1)=2,\ f_0(2)=3,\ f_0(3)=3.$ $\\$

It suffices to compute the cochain map $f^0$ for

• all basic $0$-chains of $G$, $a=p$, and
• all basic $0$-cochains of $G$, $t=q^*$; $\\$

with $p,q=0, ...,3$. We use the formula: $$f^0(q^*)(p):=q^*f_0(p),$$ with the latter equal to $0$ (the number, not the node) unless $q=f_0(p)$. Then, $f^0(q^*)(p)=0$ unless $q=p+1$ or $q=p=3$. The answer is:

• $f^0(0^*)=0$ (i.e., it's trivial);
• $f^0(q^*)=(q-1)^*,\ q=1,2$;
• $f^0(3^*)=3^*$. $\\$

We next compare the matrices: $$f_0=\left[ \begin{array}{ccccc} 0&0&0&0\\ 1&0&0&0\\ 0&1&0&0\\ 0&0&1&1 \end{array}\right], \quad f^0=\left[ \begin{array}{ccccc} 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ 0&0&0&1 \end{array}\right]. $$ The second matrix is the transposes of the first!

Second, the edges. We have

• $f_1(01)=12,\ f_1(12)=23,\ f_1(23)=0.$ $\\$

It suffices to compute the cochain map $f^1$ for

• all basic $1$-chains of $G$, $a=p$, and
• all basic $1$-cochains of $G$, $t=q^*$; $\\$

with $p,q=01,12,23$. We use the above formula: $$f^1(q^*)(p):=q^*f_1(p),$$ which is equal to $0$ unless $q=f_1(p)\ne 0$. The answer is:

• $f^1(01^*)=0$;
• $f^1\big( [m,m+1]^* \big)=[m-1,m]^*,\ m=2,3$. $\\$

Compare the matrices: $$f_1=\left[ \begin{array}{cccc} 0&0&0\\ 1&0&0\\ 0&1&0 \end{array}\right], \quad f^1=\left[ \begin{array}{cccc} 0&1&0\\ 0&0&1\\ 0&0&0 \end{array}\right]. $$ Once again, they are the transposes of each other. $\square$

Exercise. Compute the cochain maps of other specific choices of $f$ -- shift, flip, fold -- for the graph in the last example.

To make sense of the formula in the definition, let's use the integral notation above ($k=1$): $$ \displaystyle\int_a f^1(t)= \displaystyle\int_{f_1(a)}t.$$ Then, if we set $a=AB$, we have $$ \displaystyle\int_A^B f^1(t)= \displaystyle\int_{f(A)}^{f(B)}t.$$ But this is just the formula of integration by substitution...

The coboundary operator

Recall that the boundary operator $$\partial: C_1(G) \to C_0(G) $$ is set by its value for each edge: $$\partial (AB) = A+B.$$ What happens to the cochains? Just as in the last subsection, we expect that the arrows will be reversed, in a “dual” way.

Suppose $s$ is a $1$-cochain in $G$ and $Q$ a $0$-cochain. Then the relation between them is seen in the following commutative diagram, similar to the one in the last subsection: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccccccccc} C_1(G)&\ra{s}& {\bf Z}_2 \\ \da{\partial}& & || \\ C_0(G)&\ra{Q}& {\bf Z}_2 \end{array}$$

Definition. The coboundary operator of a graph $G$ is the homomorphism: $$d=\partial ^*:C^0(G)\to C^1(G),$$ defined by $$d(Q)(a):=Q\partial (a),$$ for any $1$-chain $a$ and any $0$-cochain $Q$ in $G$.

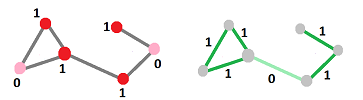
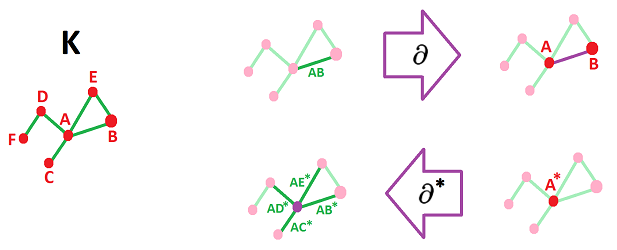
Example. Here is an example:

Our claim is that $$dA^*=AB^*+AC^*+AD^*+AE^*.$$ We prove it by evaluating $dA^*$ for each of the four basic $1$-chains: $$dA^*(AB)=(AB^*+AC^*+AD^*+AE^*)(AB)=1+0+0+0=1,$$ and, similarly: $$dA^*(AC)=1,\ dA^*(AD)=1,\ dA^*(AE)=1.$$ We can also use the definition with $Q=A^*$:

$\square$

Exercise. Generalize this example.

Example. Consider the boundary operator for this graph one more time:

Then: $$\begin{array}{lllll} \partial \Big([1,0,0,0]^T\Big)=[1,1,0,0]^T, &d \Big([1,0,0,0] \Big)=[1,0,1,0];\\ \partial \Big([0,1,0,0]^T\Big)=[0,1,1,0]^T, &d \Big([0,1,0,0] \Big)=[1,1,0,0];\\ \partial \Big([0,0,1,0]^T\Big)=[1,0,1,0]^T, &d \Big([0,0,1,0] \Big)=[0,1,1,1];\\ \partial \Big([0,0,0,1]^T\Big)=[0,0,1,1]^T, &d \Big([0,0,0,1] \Big)=[0,0,0,1]; \end{array}$$

Therefore, the matrices are $$\partial = \left[ \begin{array}{llllll} 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 \end{array} \right], \quad d = \left[ \begin{array}{llllll} 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \end{array} \right].$$ They are the transposes of each other. $\square$

Exercise. Provide the details of the computations above.

To make sense of the formula in the definition we use the integral interpretation again, with $a=AB$: $$ \displaystyle\int_{AB} dQ= \displaystyle\int_{\partial (AB)}Q= \displaystyle\int_{A+B}Q=Q(A)+Q(B).$$ But that's the (binary) Fundamental Theorem of Calculus! That's why, when we think of cochains as differential forms, $d$ is called the exterior derivative (or the differential). In this sense, $Q$ is an antiderivative of $dQ$.

We are in a position to conjecture that this isn't a coincidence...