This site is being phased out.
Calculus I -- Fall 2017
MTH 229 - Calculus with Analytic Geometry I (CT). An introduction to analytic geometry. Limits, derivatives, and integrals of the elementary functions of one variable, including the transcendental functions. (PR: MTH ACT of 27 or above, or MTH 130 and 122, or MTH 127 and 122, or MTH 132) This course meets a Core I/Critical Thinking requirement.
- Time and Place: 5:00 pm - 5:50 pm MW and 5:00 pm - 6:15 pm TR at 518 Smith Hall.
- Instructor: Peter Saveliev (call me Peter).
- Office: Smith Hall 713.
- Office Hours: MW 3:00 - 5:00, or by appointment.
- Office Phone: x4639.
- E-mail: saveliev@marshall.edu.
- Class Web-Page: math01.com.
- Prerequisites: fluency with algebra, good understanding of functions.
- Text: Calculus by Stewart and the lecture notes.
- Goals: good understanding of limits, the derivative and the integral, fluent differentiation.
- Computer Restrictions: graphic calculator TI-83 or TI-83+.
- Activities: the student will practice each outcome via the homework given in the textbook and online.
- Evaluation: the student achievement of each outcome will be assessed via:
- in-class quizzes: taken from the textbook's exercise sets;
- online quizzes: based on the course material, provided by Webwork, http://webwork.marshall.edu/webwork2/F17-Math-229-Saveliev/;
- in-class tests: based on the textbook's exercises;
- projects: written applications of calculus in science and engineering.
- Grade Breakdown:
- participation: $5\%$,
- quizzes: $25\%$,
- project: $20\%$,
- midterm: $20\%$,
- final exam: $30\% $,
i.e., the total score is the following weighted average of the five scores: $$\text{TOTAL }= .05 \times P + .25\times Q + .20\times P + .20\times M + .30\times F.$$
For other details, see Course policy.
Contents
Lectures
They will appear here as the course progresses.
Notes:
YouTube channel Calculus I
Chapters:
- Sequences and their limits
- Limits and continuity
- The derivative
- Differentiation
- Differentiable calculus
- Applications of differential calculus
- The integral
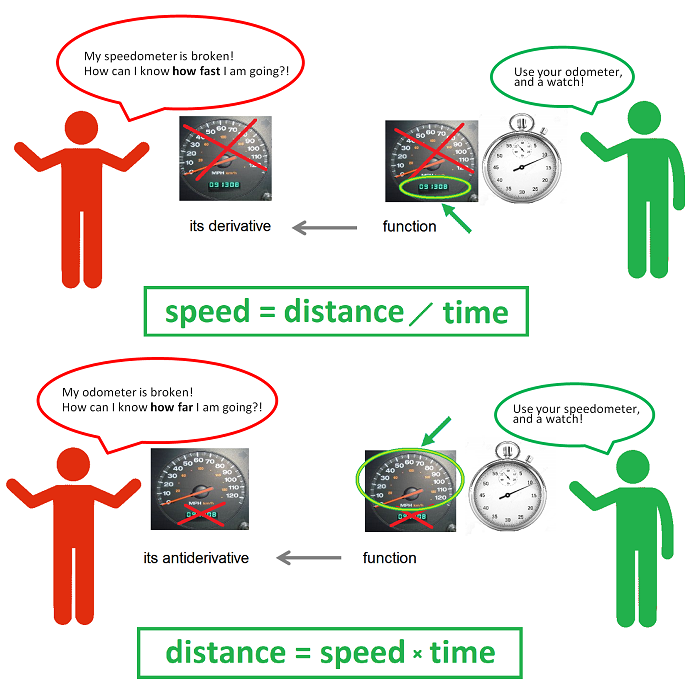
Calculus in one picture...
Projects
The details and the project statements are here: Calculus Illustrated -- Projects.
Instructions:
- A group should contain one person.
- There may be short presentations half-way.
- Your submission should be both on paper and in a digital format such as PDF (it will be linked here).
- It is a good idea to go digital from the beginning; for example, write with Latex or MS Word, draw with MS Paint, analyze data with MS Excel or Google spreadsheets.
- Include: the name, the title, introduction, conclusions, labeled pictures and tables, references, etc.
- The Excel file with the “free fall” equations is here for download, some explanations are here.
- Due date: one week before the last class: Thursday, November 30th
Assignments:
- 1. Gavin (11c). In this project, I will use Calculus to determine the best angle to use if you are trying to reach a point that is 10 miles north and 10 miles east of your starting location. If the first half of the hike was a steady mountain and the rest leveled off as the hill plateaued, which initial angle for ascension would be necessary to ensure the fastest hiking time? We can imagine that this could be a contest and the winner would receive a million dollars. There was one problem; everybody hiked at the same pace depending on the inclination of the earth. For this example, I will set the hill velocity at v₁=3 miles/hour and the flat ground velocity at v₂=6 miles/hour. The Pythagorean Theorem will be used to create equations for the two-line segments which represent the hiker’s path. The first line segment (the path that lies on the hill) will be labeled as A and the line that lies on flat ground will be labeled as B. As for the x variable that our equations will be incorporating, it will stand for the distance east that the hiker is at once he completely ascends the hill. The point at which the hill flattens out is 5 miles north from the origin. This means that the minimum distance of the hillside that the hiker will be climbing is 7.07 miles if traveling straight up the hill. This still does not take away at the total displacement of location. The displacement will remain 10 miles away from the origin. I plan to use excel graphs to accurately represent different trials of hikers to prove my answer. The hikers will choose different x values, which will ultimately affect their total hiking time.
- 2. Malik (11b)
- 3. Travis (10b) In this project, the objective is to determine if it was possible for Archimedes to have set fire to Roman ships by redirecting the sunlight with reflective shields. For testing/modeling purposes, I will generate a simulation to test the objective from an Excel and MicrostationV8i. Using the law of reflection and tangencies to accompany my findings, could it have been that Archimedes was successful in his defensive tactic using reflective shields to burn the Roman ships? Ultimately, I will test the objective myself and have a video reference.
- 4. Logan (5b). Can a sailing boat go in the direction opposite to the direction of the wind? For my final project in Calculus class, I have been assigned the action of a sailboat sailing against the flow direction of the wind. The sail of a boat works almost in the same fashion as wings do on a plane. When air flows over a wing from front to back, the wind that flows over the top of the wing travels farther than the wind that travels underneath, which creates a pressure difference, and this is what lifts the plane. For a sailboat, wind blowing at an angle against the boat inflates the sail. The sail forms a similar shape to a plane wing, which creates a difference in pressure that pushes the sail in a direction perpendicular to the wind. Theoretically, this can be done, but it still needs to be tested experimentally. To do this, one would have to calculate the lift/drag ratio, just like one would for a plane wing, where “lift” can be translated into “push”, as well as the angle of attack, α. A sail requires a relatively large value for α, between 15 and 25 degrees, to give enough drive to overcome the total amount of drag from the sail, hull, and keel of the boat.
- 5. Branden (2b). For my calculus project, I have been tasked with trying to find out if a man can run from one table to another without touching the floor by stepping on a bouncing ball. I will attempt to solve this problem by first finding the average and instantaneous velocity of the man as he makes the full run and as he steps on the ball respectively. I will also calculate when the ball must be dropped so that it does not hit the runner, and I will find out how high the ball must be dropped from so that its bounce will bring it to the exact height of the tables so that the runner can cross it. I will be using Microsoft excel to provide a visual representation of my math.
Description
List of topics
- Brief review of basic concepts of algebra
- Number systems. Distance formula. Slope of a line. Standard equations of lines.
- A library of functions
- The basic equations and qualitative behavior of linear functions, power functions, polynomial functions, rational functions, exponential and logarithmic functions, and trigonometric functions.
- Limits and applications
- The limit of a function at a point. One-sided limits. Continuity and the intermediate value theorem. Infinite limits. Limits at infinity. Applications of limits to engineering and science.
- Differentiation and applications
- Definition of the derivative at a point and on an interval. Slope of a tangent line. Derivatives of polynomials. Derivatives of trigonometric functions. Derivatives of exponential and logarithmic functions. Rules for differentiation. Mean value theorem. Implicit differentiation. Maxima and minima. Critical points and intervals of increase and decrease. Concavity and inflection points. Newton's Method. Differentials and linear approximation. Applications of derivatives to engineering and science.
- Integration and applications
- Area as an integral. Antiderivatives. Riemann sums. Definite integrals as limits of Riemann sums. The Fundamental Theorem of Calculus. The substitution method for integrals. Applications of integrals to engineering and science.
Learner outcomes
- 1. Students will be able to evaluate limits, derivatives, and integrals symbolically.
- 2. Students will be able to approximate limits, derivatives, and definite integrals from tabular and graphical data.
- 3. Students will be familiar with the definitions of limits, derivatives, and integrals; be able to apply these definitions to test properties of these concepts; and be able to produce verbal arguments and examples showing that basic properties hold or do not hold.
- 4. Students will be able to apply the techniques of calculus to answer questions about the analytic geometry of functions, including vertical and horizontal asymptotes, tangent lines, local extrema, and global extrema.
- 5. Students will be able to verbally explain the meaning of limits, derivatives, and integrals in their own words, both in general terms and in the context of specific problems.
- 6. Students will be able to select or construct an appropriate function to model an applied situation for which calculus is applicable, based on a verbal description of the situation.
- 7. Students will be able to apply techniques of calculus to solve applied problems from fields such as engineering and the sciences.
- 8. Students will be able to interpret symbolic and numerical results in real-world terms, and analyze the validity of their results in a real-world setting.
Course goals
- To give students an understanding of the fundamental concepts of calculus and an appreciation of its many applications.
- To develop critical thinking skills by asking students to convert real-world problems into forms suitable for calculus, and interpret the results of calculus in real-world terms.
- To provide students with a deeper understanding of the mathematics that is used in their science and engineering courses.
- To develop facility in using graphing calculators and computers to solve mathematics problems.
- To satisfy program requirements.
Tutoring
The tutoring lab is in Smith Hall 625. It will be open Monday through Thursday from 10am to 4pm and 5:00pm to 6:30pm, and on Friday from 10:00am to noon. As usual, we offer free drop-in tutoring for math and statistics classes through Calc 3.
The lab will open on the second week of classes, beginning August 28 and running through the end of the semester. The lab is not open during finals week.
Also, the university tutoring center is in Smith Communications on the second floor.
Exams
- Calculus I -- Fall 2017 -- midterm: Wednesday, October 11.
- Calculus I -- Fall 2017 -- final: Monday, December 11, 5-7 pm, same place.
Each old exam below is a small sample of the types of problems that may appear:
- 2017: Calculus I -- Spring 2017 -- midterm, Calculus I -- Spring 2017 -- final
- 2016: Calculus I -- Fall 2016 -- midterm, Calculus I -- Fall 2016 -- final
- 2012: Calculus I -- Fall 2012 -- midterm, Calculus I -- Fall 2012 -- final exam
- 2010: Calculus 1: midterm 1, Calculus 1: midterm 2, Calculus 1: final
- 2008: Calculus 1: test 1, Calculus 1: test 2, Calculus 1: test 3, Calculus 1: final exam