This site is being phased out.
Calculus I -- Fall 2012 -- midterm
Midterm
Name:_________________________
- Show enough work to justify your answers
- Write the problems in the given order, each problem on a separate page.
1. Sketch the graph of a function $f$ with the following features: (a) it has a removable discontinuity at $x=-1$; (b) it has a vertical asymptote at $x=1$; (c) it is continuous but not differentiable at $x=3$; (d) it is differentiable everywhere else; (e) it has no horizontal asymptotes.
2. Compute the two one-sided limits of the function below at $x=-1$ and $x=3$: \[ f(x)=\left\{ \begin{align} {}% -x+1 & \text{ if } x<-1\\ x^{2}+1 & \text{ if } -1\leq x<3\\ e^x & \text{ if }x>3% \end{align} \ \right. . \]
3. (a) Represent function $h(x)=e^{x^3-1}$, as a composition of two functions f and g, (b) Provide the formulas for the two possible compositions of the functions: "take the logarithm of" and "take the square root of".
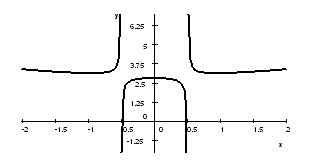
4. The graph of $f$ is given below. It has asymptotes. Describe them as limits. Hint: use both $+ \infty$ and $- \infty$.
5. (a) State the the $ɛ-δ$ definition of limit. (b) Use the definition to prove that $\lim _{x→2} (x/2-1)=0$.
6. From the definition, compute the derivative of $f(x)=2x²-1$ at $a=1$.
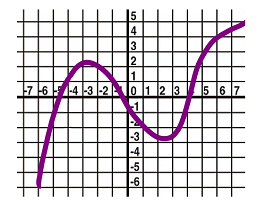
7. The graph of a function $f(x)$ is given below. Estimate the values of the derivative $f'(x)$ for $x=-3,1$, and $5$.
8. Find the horizontal asymptote of the function $$f(x)=\frac{3x^3-1}{x(5x²-7)}$$ by computing a certain limit.
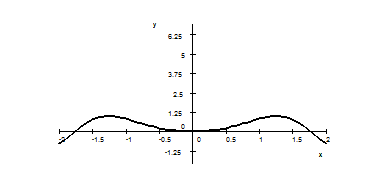
9. The graph of function $f$ is given below. Sketch the graph of the derivative $f^{\prime}(x)$ .
10. Calculate the derivative of $$ f(x) = x^{\pi} + \pi^{x} + x + \pi.$$ Indicate the rules you use.
11. Differentiate this $$g(t)=t \cos t \sin t.$$