Calculus III -- Spring 2015 -- midterm

Name:_________________________ $\qquad$ 8 problems, 10 points each

• Justify every step you make with as thorough an explanation as possible, in English.
• Unless requested, no decimal representation of the answers is necessary.
• Start every problem at the top of the page.

$\bullet$ 1. Sketch the following parametric curve: $x=|\cos t|,y=|\sin t|, -\infty <t <+\infty$. Describe the curve and the motion.

$\bullet$ 2. Find the best linear approximation of the function $f(x,y)=xy^2$ at the point $(0,1)$.

$\bullet$ 3. Find the directional derivative of the function $f(x,y)=2x^2-3y$ at the point $(1,1)$ in the direction of the vector $<1,0>$.

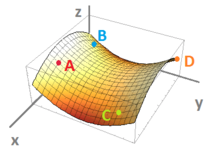
$\bullet$ 4. Sketch the contour (level) curves of the function shown below, along with points $A,B,C,D$, on the $xy$-plane:

$\bullet$ 5. Find the line tangent to the curve $r(t)=<t^{5},t^{4},t^{3}>$ at the point $(1,1,1)$.

$\bullet$ 6. Represent the function $h(x,y)= \sqrt{x^2y-1}$ as the composition of two functions. Find its derivatives using the Chain Rule.

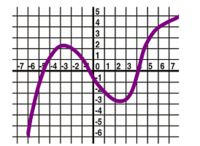
$\bullet$ 7. The graph of function $y=g(x)$ of one variable is shown below. Suppose now that $z=f(x,y)=g(x)$ is a function of two variables, which depends only on $x$, given by the same formula. Find all points where the gradient of $f$ is equal to $0$.

$\bullet$ 8. Find all critical points of the function $f(x,y)=2x^3-6x+y^2-2y+7$.