This site is being phased out.
Calculus III -- Spring 2015 -- final exam
Name:_________________________ $\qquad$ 12 problems, 10 points each
- Justify every step you make with as thorough an explanation as possible, in English.
- Unless requested, no decimal representation of the answers is necessary.
- Start every problem at the top of the page.
$\bullet$ 1. Sketch the following parametric curve: $x=t^3,y=t^5,\ -1\le t \le 1$. Is this a regular parametrization?
$\bullet$ 2. (a) Give the definition of the curvature (as a certain derivative). (b) Use the definition to compute the curvature of a circle of radius $R$.
$\bullet$ 3. Find the gradient of the function $f(x,y)=x^2y^{-3}$ at the point $(1,1)$. Use this information to sketch the graph of $f$ in the vicinity of this point. Explain.
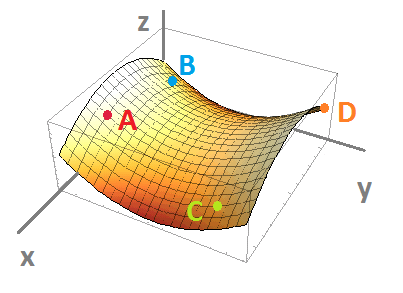
$\bullet$ 4. The graph of a function of two variables $z=f(x,y)$ is given below along with four points on the graph. Provide the signs of the partial derivatives of $f$ at these points. For example, $\frac{\partial f}{\partial x}<0$ at point $A$.
$\bullet$ 5. A function of two variables is given by $f(x,y)=xy^2$. (a) Find the linear approximation of $f$ around the point $(1,1)$. (b) Represent the graph of $f$ as a parametric surface and find the plane tangent to this surface at the point $(1,1,1)$.
$\bullet$ 6. State the chain rule, for the case of the composition of a function of two variables and a function of one variable.
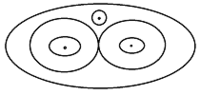
$\bullet$ 7. The contour (level) curves for a function are given below. They are equally spaced. Sketch a possible graph that produced it and describe it.
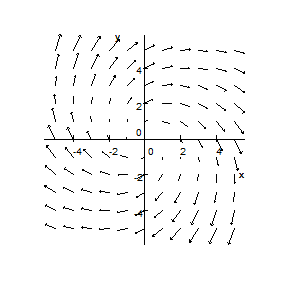
$\bullet$ 8. State the path-independence property. Does the vector field shown below satisfy the path-independence property? Explain.
$\bullet$ 9. Find all critical points of the function $f(x,y)=2x^3-6x+y^2-2y+7$.
$\bullet$ 10. This is the formula of Green's Theorem: $$\oint_{C} F\cdot dr = \iint_{D} \left(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}\right)\, dA. $$ Explain its parts and relations between them. Provide a sketch.
$\bullet$ 11. Compute this integral: $$\iiint_D(y+z)dV,$$ where region $D$ is bounded by: $y=0,y=x^2,x=1,z=0,z=2$.
$\bullet$ 12. (1) Represent the circle of radius $1$ centered at $0$ as a parametric curve. (2) Find the tangent line to this circle at the point $(\sqrt{2}/2,\sqrt{2}/2)$. (3) Compute the flux of the vector field $F=< 2,1 >$ across the part of the circle that lies in the first quadrant.
$\bullet$ Extra credit problem. (5 points, no partial credit) Suppose you are towing a trailer-home. During the first few minutes, every time you look at the rear view mirror you can see only the lower part of the home. Later, every time you look you can see only the top part. Discuss the profile of the road.