Applications of derivative: optimization

Farmer's fence revisited

Problem

Recall: A farmer with 100 yards of fencing needs to build a rectangular enclosure with the largest possible area, where $x$ is the width, $y$ is the depth and $A$ is the area.

We use geometry to connect these variables. $$ A = xy. $$ Then use the conditions to get more information: $$ x + y + x + y = 100. $$ The problem has become mathematical: $$\begin{aligned} \text{Given }2x + 2y &= 100, \quad x \geq 0, \quad y \geq 0 \\ \text{Maximize } A &= xy \end{aligned}$$

Solution.

We have $$ y = 50 - x .$$ Substitute to create a function of a single variable: $$ A = x(50-x) .$$ Find the global maximum on $[0,\infty)$ of $$A = -x^{2} + 50 x.$$ We turn to calculus: $$A^{\prime} = -2x + 50 = 0 $$ and solve for $x$. $$ x = 25. $$ Substituting $x$, we get $$\begin{aligned} y &= 50 - x \\ &= 50 - 25 = 25 \end{aligned}$$ The maximum area is $$ A = xy = 25\cdot 25 = 625 $$

Answer (in the language of the problem):

The enclosure should be $25 \times 25$ yards and its area is 625 sq. yards.

Optimization in algebra

Find two numbers whose difference is 100 and the product is a minimum.

Step 1

Deconstruct: (#1 two numbers) whose (#2 difference is 100) and (#3 the product is a minimum)

1. Introduce the variables: $x$ is the first number, $y$ is the second number.
2. $x - y = 100$
3. $P$ is the product: $P=xy$, minimize $P$.

That's a math problem now.

Step 2

Eliminate the extra variables to create a function of single variable to be maximized or minimized.

Equation connecting the variables: $$ x - y = 100.$$ A function of the variables: $$ P = xy$$

Solve the equation for $y$: $$ y = x - 100 .$$ Eliminate $y$ from $P$ by substitution: $$ P = xy = x(x - 100). $$

Step 3

Optimize this function $$\begin{aligned} P(x) & = x^{2} - 100x \\ P^{\prime} &= 2x - 100 \\ &= 2x - 100 = 0 \end{aligned}$$

That's a parabola:

Solve for $x$: $$x = 50.$$

Step 4

Provide the answer using the original language of the problem: Substitute $x$ into $y$, $$\begin{aligned} y &= x - 100 \\ &= 50 - 100 \\ &= -50 \end{aligned}$$

Answer:

50 and -50

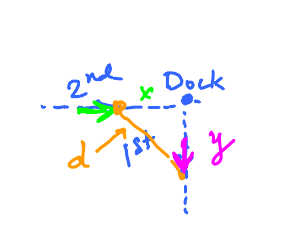
Distance between boats

1st Boat:

• Leaves at 2:00,
• goes south,
• at 20 km/h

2nd boat:

• Goes east,
• at 15km/h,
• reaches the dock at 3pm.

Q: When were they the closest to each other?

Solution.

We will "translate" the above items one by one into math.

We need variables for that. Let $t$ be the time, start 0 (noon).

We need to record their locations. These will be the variables:

1. $x$ is the distance of 2nd boat to the dock (green).
2. $y$ is the distance of 1st boat to the dock (pink).
3. $d$ is the distance between them (orange).

We have four variables, as $x$, $y$, $d$ are functions of $t$. From geometry, $$ x^{2} + y^{2} = d^{2} .$$ (Pythagorean Theorem)

Translate the setup items:

$$\left.\begin{aligned} y(2) & = 0 \\ y^{\prime}(t) &= 20 \end{aligned} \right\} \qquad \text{Point slope form: } y - 0 = 20(t - 2) $$

$$\left.\begin{aligned} x(3) & = 0 \\ x^{\prime}(t) &= 15 \end{aligned} \right\} \qquad \text{Point slope form: } x - 0 = 15(t - 3) $$

Task: Minimize $d$.

Rewrite $$\begin{aligned} y &= 20t - 40 \\ x &= 15 t - 45 \\ d^{2} & = x^{2} + y^{2}, \quad \text{minimize}. \end{aligned}$$

Substitute: $$ d = \sqrt{x^{2} + y^{2}} = \sqrt{(15t - 45)^{2} + (20t - 40)^{2}} $$ Find the global minimum of this function. $$\begin{aligned} d(t) &= \sqrt{ 225t^{2} - 1250t + 2025 + 400t^{2} - 1600t + 1600} \\ &= \sqrt{625t^{2} -2850 t + 3625} \\ \text{CR } d^{\prime}(t) &= \frac{1}{2\sqrt{625t^{2} -2850 t + 3625}}(1250 t - 2850) \\ &= 0 \end{aligned}$$ We solve: $$1250t - 2850 = 0,$$ so $$ t = \frac{2850}{1250} = 2.28. $$

Answer:

At approximately 2:20 pm.

Test the answer

at 2:30, the distance is $$\sqrt{7.5^{2} + 10^{2}} = 12.5,$$

which makes sense...

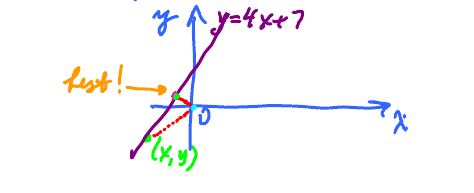
Optimization in geometry

Find a point on the line $y=4x + 7$ closest to the origin.

Let a point on the line be given by $(x,y)$, its coordinates. Then they are connected by the equation of the line: $$ y = 4x + 7 .$$ Let $d$ be the distance to $O$, then $$ d^{2} = x^{2} + y^{2}.$$ That's the function to minimize.

Substituting $$ d^{2} + x^{2} (4x + 7)^{2}. $$ So $$ d(x) = \sqrt{x^{2} + (4x + 7)^{2}} $$ Find the global maximum. Exercise...

Maximize Profit

Necklaces were sold last summer at $10 each and 20 per day. This summer, they were sold at $11 each and 18 per day.

What is the Demand Function?

We assume it's linear. Let $p$ be the price and $D$ be the sales or demand (for this price). Then

1. $D(10) = 20,$
2. $D(11) = 18.$

Find $D = D(p).$ The slope is $$\frac{\text{rise}}{\text{run}} = \frac{-2}{1} = -2. $$ The point-slope formula is $$\begin{aligned} y - 20 &= -2(p - 10) \\ y &= -2p + 20 + 20 \\ &= -2p + 40 \\ \therefore D(p) &= -2p + 40 \end{aligned}$$

Now, if the cost is $6 per necklace, what is the maximum profit can you make?

Let $C$ be the cost per necklace: $C=6$.
Let $D$ be the profit as a function of $p$.
Let $R$ be the revenue: $$\begin{aligned} R &= D(p)\cdot p \\ &= (-2p + 40) p \\ &= -2 p^{2} + 40p \end{aligned}$$ Then $$\begin{aligned} P &= R - \overbrace{C\cdot D}^{\text{total cost}} \\ &= -2 p^{2} + 40p - 6(-2p + 40) \\ &= -2 p^{2} + 40p + 12p -240 \\ P(p) &= \underbrace{-2 p^{2} + 52p -240}_{\text{upside down parabola}} \end{aligned}$$ Find its global maximum: $$\begin{aligned} P^{\prime} &= -4p + 52 \\ &= 0. \end{aligned}$$ Solve for $p$: $$p = \frac{52}{4} = 13. $$

Answer:

The price should be $13 per unit.