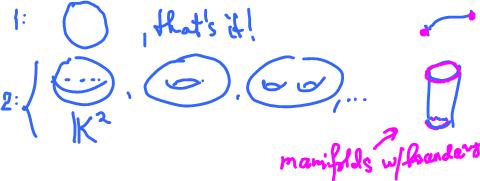This site is being phased out.
Surface
Redirect to:
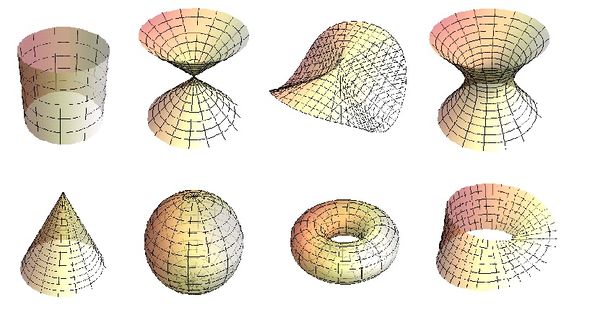
Well known examples of surfaces are:
- the plane,
- the paraboloid,
- the cylinder,
- the sphere,
- the torus,
- the Klein bottle,
- the projective plane.
What do they have in common? Locally, they look like disks. Just like the Earth looks like a plane if you don't move far.
Since disks are homeomorphic to the plane which is the $2$-dimensional Euclidean space ${\bf R}^2$, we can say that surfaces are "locally Euclidean".
Thus surfaces are $2$-dimensional manifolds.
Definition. A topological space $S$ is called a surface (without boundary) if $S$ is Hausdorff and every point in $S$ has a neighborhood homeomorphic to ${\bf R}^2$.
Exercise. One of the surfaces depicted above isn't, which one? Consider also something that looks like a book?
Theorem. The disjoint union of two surfaces is a surface.
Because of this theorem we concentrate on path-connected surfaces. We will also concentrate only on compact surfaces, since non-compact surfaces can't be represented as finite cell complexes.
While there is only one compact connected $1$-manifold, there is a variety of surfaces.
Clearly, there are many "surfaces" that aren't $2$-manifolds as defined:
- the closed disk,
- any of the surfaces listed at the top with holes punched through,
- the cylinder,
- the Mobius band.
The difference is that these surfaces have "edges" aka boundaries.
Definition. A topological space $S$ is called a surface with boundary, if $S$ is Hausdorff and every point in $S$ has a neighborhood homeomorphic to:
- either the whole $2$-dimensional Euclidean space ${\bf R}^2$
- or the half-space $\{x \in {\bf R}^2 \colon x_1 \geq 0 \}$.
(In other words, these are disks and half-disks.) The latter points form the boundary of the surface.
For more examples, see Quotients of manifolds.
A surface is called non-orientable is it contains the Mobius band:
- Mobius band, Klein bottle, projective plane, etc.
The rest are orientable:
Punching holes in a surface without boundary will create a variety of surfaces with boundary:
The boundaries of the holes are circles, hence the boundary of these surfaces are too. Are all surfaces with boundary like that?
Consider the Mobius band. You travel along the "lower edge" from $A$ to $B$, and next you are at $B$ on the "upper" edge, the you travel along it to $A$. You come back where you started. So, indeed, the boundary of the Mobius band is homeomorphic to the circle.
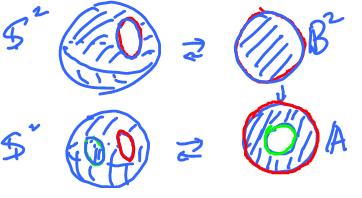
Theorem. The boundary of a compact surface $S$ is
- a closed subset of $S$,
- a compact $1$-manifold without boundary,
- the union of a finite number of circles.
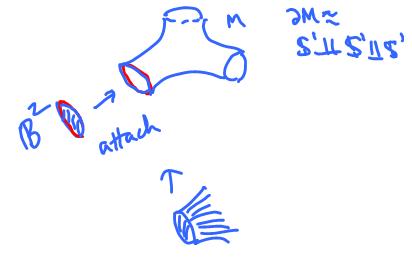
It follows that a surface with boundary can be easily turned into a surface without boundary by attaching a few disks:
Exercise. What happens if you attach the disk to the boundary of the Mobius band? Prove via a diagram. Solution: ![]()
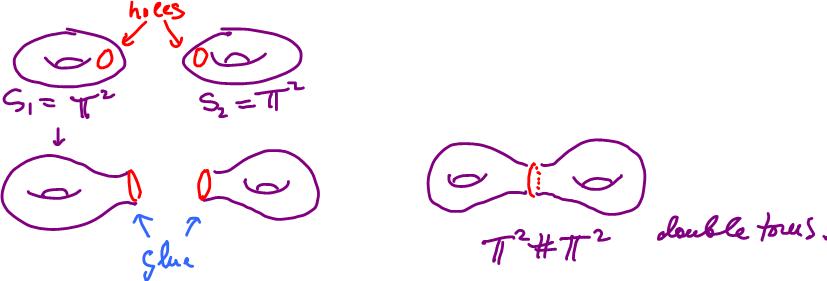
Further, any two surfaces can be attached to each other by punching holes in them and then gluing them together along these edges. For example, this is how you create the double torus by attaching two tori to each other in this fashion.
This construction is called the connected sum $S_1 \# S_2$ of surfaces $S_1, S_2$.
Theorem (Classification of surfaces). (1) A compact connected surface is homeomorphic to
- the sphere, or
- the connected sum of of $n$ tori, or
- the connected sum of of $n$ projective planes.
(2) These options are not homeomorphic.
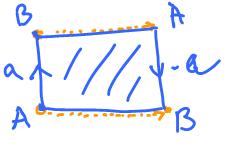
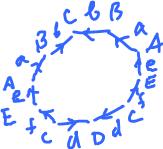
Every surface (without boundary) can be represented as polygon with the edges glued together as in this diagram:
Every edge has to appear twice (why?). What about vertices?
Exercise. Cut a hole in the middle of the projective plane and represent the result as a cell complex with a single $2$-cell (standard diagram for surfaces). What is it? Solution: ![]()
See also Triangulations of surfaces.