This site is being phased out.
Properties of the exterior derivative
Redirect to:
Contents
Leibniz formula, the product rule for exterior derivative
Since $d \colon \Omega^k \rightarrow \Omega^{k+1}$ is a function between vector spaces, so we already know that $d$ is a linear operator: $$d(a \varphi + b \psi) = a d\varphi + b d\psi, a, b \in {\bf R}, \varphi, \psi \in \Omega^k.$$
Now we are interested in an analogue of the Product Rule from Calc 1 for the wedge product.
In other words, find $d(\varphi \wedge \psi) = ?$ in terms of $d \varphi$, $d \psi$, $\varphi$, $\psi$.
First, for $\varphi, \psi \in \Omega^0$, we have the familiar Product Rule: $$(\varphi \psi)' = \varphi ' \psi + \varphi \psi '.$$ It can be rewritten for the exterior derivative: $$d(\varphi \psi) = d\varphi \psi + \varphi d \psi,$$ or $$d(\varphi \wedge \psi) = d\varphi \wedge \psi + \varphi \wedge d \psi,$$ This gives us an idea what the general rule should look like: the sum of the cross (wedge) products, in the same order.
Next, we continue with $\varphi \in \Omega^k$ and $\psi \in \Omega^m$. We assume that
- $\varphi = A dX$ and
- $\psi = B dY$,
where $A,B$ are continuously differentiable functions and $dX,dY$ are basis elements of $ \Omega^k,\Omega^m$ respectively. Those could be $dx,dy$, or $dxdy,dydz$, etc. Then, by definition of exterior derivative, we have
- $d\varphi = dA \wedge dX$ and
- $d\psi = dB \wedge dY$,
In addition to this, we'll use the skew-commutativity of $\wedge$: $$f^k \wedge g^m = (-1)^{km} g^m \wedge f^k.$$
Then, we compute $$\begin{align*} d(\varphi \wedge \psi) &= d(A dX \wedge B dY) \\ {\rm (linearity \hspace{3pt} of \hspace{3pt}} \wedge) &=d(AB dX \wedge dY) \\ {\rm (definition \hspace{3pt} of \hspace{3pt} d)} &=d(AB) \wedge dX \wedge dY \\ {\rm (Product \hspace{3pt} Rule)} &=(A dB + B dA) \wedge dX \wedge dY \\ &=A dB \wedge dX \wedge dY + B \wedge dA \wedge dX \wedge dY \\ &{\rm (note:} dB \in \Omega ^1,dX \in \Omega ^k) \\ {\rm (skew-commutativity)} &=(-1)^{1 k}A dX \wedge dB \wedge dY + dA \wedge dX \wedge B \wedge dY \\ {\rm (substitute)}&=(-1)^k \varphi \wedge d \psi + d \varphi \wedge \psi. \end{align*}$$
Since we have proved the formula for the basis elements, we have proved it for all forms:
Theorem (Product Rule - Leibniz Rule): For $\varphi \in \Omega^k$ and $\psi \in \Omega^m$, we have $$d(\varphi \wedge \psi) = d \varphi \wedge \psi + (-1)^k \varphi \wedge d \varphi.$$ or simply $$d(\varphi^k \wedge \psi^m) = d \varphi^k \wedge \psi^m + (-1)^k \varphi^k \wedge d \psi^m.$$
The topological property of the exterior derivative
The property that follows (via the Stokes Theorem) from the topological identity: $$\partial\partial=0$$ is $$dd=0,$$ or
(What? No second derivatives?!)
Theorem. $d(d\varphi) = 0$ for any $C^2$-form $\varphi \in \Omega^k$.
To clarify we make these two operators distinct, add subscripts, when necessary. Then our theorem is restated: $$d_k d_{k-1} = 0,k=1,2...$$
What we have is the composition of two linear operators: $$d_{k+1}d_k=0 \colon \Omega^k \rightarrow \Omega^{k+2}$$ and it is trivial.
Let's prove this property in $3$-space using the formulas above.
First, $0$-forms. Suppose $F$ is a continuously differential function of $3$ variables. Then, $$ddF = d(F_xdx+F_ydy+F_zdz)$$ ... by the first formula $$=dF_xdx+dF_ydy+dF_zdz$$ $$=(F_{xx}dx+F_{yx}dy+F_{zx}dz)dx+...$$ ... by the second formula $$=(F_{xx}dxdx+F_{yx}dydx+F_{zx}dzdx)+...$$ $$=(0+F_{yx}dydx+F_{zx}dzdx)+...$$ ... by anti-symmetry $$=(F_{yx}dydx+F_{zx}dzdx)+(F_{xy}dxdy+F_{zy}dzdy)+(F_{xz}dxdz+F_{yz}dydz)$$ $$=(-F_{yx}+F_{xy})dxdy+(-F_{zy}+F_{zy})dydz+(-F_{zx}+F_{xz})dxdz$$ ... by anti-symmetry $$=0dxdy+0dydz+0dxdz$$ $$=0$$ ... as all the mixed derivatives are equal by Clairaut's theorem.
For $1$-forms, let's just inspect the results of a single differentiation: $$d(F dx + G dy + H dz) = (G_x - F_y) dx \hspace{1pt} dy + (H_y - G_z) dy \hspace{1pt} dz + (F_z - H_x) dz \hspace{1pt} dx.$$ To get to $0$ we apply now the third formula, anti-symmetry, and Clairaut's theorem (below).
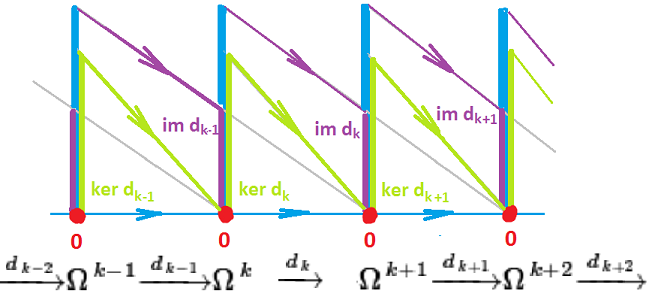
Recall the diagram of all exterior derivatives (from the last section) in this new form: $$ \ldots \stackrel{0}{\rightarrow} \Omega^0(R) \stackrel{d_0}{\rightarrow} \Omega^1(R) \stackrel{d_1}{\rightarrow} \Omega^2(R) \stackrel{d_2}{\rightarrow} \Omega^3(R) \stackrel{d_3}{\rightarrow} \ldots ,$$ where $R$ is a region. This sequence of vector spaces and linear operators (with the property) is called the de Rham complex of $R$. With the property $dd=0$, such a sequence is called a cochain complex. Warning: Unfortunately, $C^k$ stands both for $k$ times continuously differentiable functions and cochains of degree $k$.
Observe then that $dd=0$ is equivalent to $${\rm im} d_1 \subset {\rm ker} d_2 .$$ The construction is illustrated below.
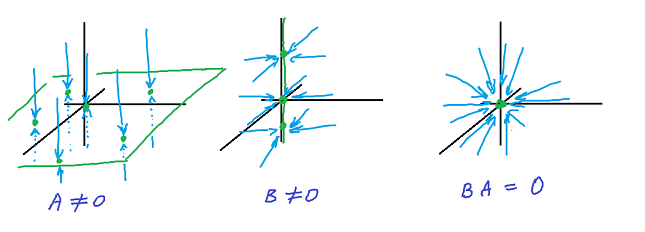
This is pure linear algebra!
Example: As an illustration, consider this example of two operators below. Neither operator is $0$, but their composition is:
Here,
- $A$ is the projection on the $xy$-plane, which isn't $0$;
- $B$ is the projection on the $z$-axis, which isn't $0$;
- $BA$ is $0$.
Proof of $dd=0$ for $1$-forms
Theorem: The composition of the exterior derivative $dd \colon \Omega^1({\bf R}^3) \rightarrow \Omega^3({\bf R}^3)$ for $C^2$-forms is $0$.
Proof: Recall $$d(A dx + Bdy + Cdz) = {\rm curl}(A,B,C) \cdot (dx \hspace{1pt} dy, dy \hspace{1pt} dz, dz \hspace{1pt} dx)$$ and $$d(U dx \hspace{1pt} dy + V dy \hspace{1pt} dz + W dz \hspace{1pt} dx) = {\rm div}(U,V,W) dx \hspace{1pt} dy \hspace{1pt} dz,$$ where ${\rm grade}$, ${\rm curl}$, and ${\rm div}$ are in terms of discrete partial derivatives.
Compute...
Let $\varphi = Adx + Bdy + Cdz \in \Omega^1({\bf R}^3)$. Then $$\begin{align*} d\varphi &= dAdx + dBdy + dCdz \\ &= (A_xdx + A_ydy + A_z dz)dx + (B_xdx + B_ydy + B_zdz)dy + (C_xdx + C_ydy+C_zdz)dz \\ &= Adx \hspace{1pt} dx + A_y dy \hspace{1pt} dy + A_z dz \hspace{1pt} dx + B_x dx \hspace{1pt} dy + B_y dy \hspace{1pt} dy + B_z dz \hspace{1pt} dy + C_x dx \hspace{1pt} dz + C_y dy \hspace{1pt} dz + C_z dz \hspace{1pt} dz \\ &= A_y dy \hspace{1pt} dx + A_z dz \hspace{1pt} dx + B_x dx \hspace{1pt} dy + B_z dz \hspace{1pt} dy + C_x dx \hspace{1pt} dz + C_y dy \hspace{1pt} dz \end{align*}$$
Note: many terms disappear because $dx \hspace{1pt} dx=dy \hspace{1pt} dy=dz \hspace{1pt} dz=0$.
$$\begin{align*} d(d \varphi) &= d(A_y)dy \hspace{1pt} dx + d(A_z)dz \hspace{1pt} dx + d(B_x)dx \hspace{1pt} dy + d(B_z)dz \hspace{1pt} dy + d(C_x)dx \hspace{1pt} dz + d(C_y)dy \hspace{1pt} dz \\ &= (A_{yx}dx + A_{yy}dy+A_{yz})dy \hspace{1pt} dx + (A_{zx}dx+A_{zy}dy+A_{zz}dz)dz \hspace{1pt} dx + (B_{xx}dx+B_{xy}dy+B_{xz}dz)dx \hspace{1pt} dy \\ &+ (B_{zx}dx+B_{zy}dy+B_{zz}dz)dz \hspace{1pt} dy + (C_{xx}dx+C_{xy}dy+C_{xz}dz)dx \hspace{1pt} dz + (C_{yx}dx+C_{yy}dy+C_{yz}dz)dy \hspace{1pt} dz \\ &= A_{yz}dz \hspace{1pt} dy \hspace{1pt} dx + A_{zy}dy \hspace{1pt} dz \hspace{1pt} dx + B_{xz}dz \hspace{1pt} dx \hspace{1pt} dy + B_{zx}dx \hspace{1pt} dz \hspace{1pt} dy + C_{xy}dy \hspace{1pt} dx \hspace{1pt} dz + C_{yx}dx \hspace{1pt} dy \hspace{1pt} dz \end{align*}$$
Recall that due to Clairaut's theorem for partial differentiation: $$A_{yz}=A_{zy},B_{xz}=B_{zx},C_{xy}=C_{yx}.$$
So, using antisymmetry...
$$\begin{align*} &= A_{zy}dz \hspace{1pt} dy \hspace{1pt} dx + A_{zy}dy \hspace{1pt} dz \hspace{1pt} dx + B_{zx} dz \hspace{1pt} dx \hspace{1pt} dy + B_{zx}dx \hspace{1pt} dz \hspace{1pt} dy + C_{yx}dy \hspace{1pt} dx \hspace{1pt} dz + C_{yx}dx \hspace{1pt} dy \hspace{1pt} dz \\ &= A_{zy}dz \hspace{1pt} dy \hspace{1pt} dx - A_{zy}dz \hspace{1pt} dy \hspace{1pt} dx + B_{zx}dz \hspace{1pt} dx \hspace{1pt} dy - B_{zx}dz \hspace{1pt} dx \hspace{1pt} dy + C_{yx}dy \hspace{1pt} dx \hspace{1pt} dz - C_{yx}dy \hspace{1pt} dx \hspace{1pt} dz \\ &= 0 + 0 + 0 = 0 \end{align*}$$ $\blacksquare$
Exercises
1. Differential equation $$\frac{dy}{dx} = \frac{f(x)}{g(y)}$$ is solved by "separation of variables" $$g(y)dy = f(x)dx$$ followed by integration. Explain the relation between these two equations.
2. Compute $df$, where $f=x^1+2x^2+...+nx^n$, on $<1,-1,...,(-1)^{n-1}>$ at $(1,2,...,1)$.
3. Prove that in ${\bf R}^n$, $$df^1 \wedge ... \wedge df^n(x) = \det \frac{\partial f^i}{\partial x^j}(x)dx^1 \wedge ... \wedge dx^n.$$
4. Write the form $df$, where $f(x) = (x^1) + (x^2)^2 + ... + (x^n)^n$, as a combination of $dx^1,...,dx^n$.