This site is being phased out.
Calculus III -- Fall 2017
MTH 231 - Calculus with Analytic Geometry III. Vectors, curves, and surfaces in space. Derivatives and integrals of functions of more than one variable. A study of the calculus of vector-valued functions. PR: MTH230. 4 hours.
- Time and Place: 2:00 pm - 2:50 pm MTWR at 509 Smith Hall.
- Instructor: Peter Saveliev (call me Peter).
- Office: Smith Hall 713.
- Office Hours: MW 3:00 - 5:00, or by appointment.
- Office Phone: x4639.
- E-mail: saveliev@marshall.edu.
- Class Web-Page: math02.com.
- Prerequisites: excellent algebra skills, good understanding of the derivative and the integral, fluent differentiation and integration.
- Text: Calculus by Rogawski and the lecture notes.
- Goals: the student will learn to analyze parametric curves, functions of several variables, and vector fields, apply these concepts and tools to study processes and patterns in physical and other sciences, become familiar with vector calculus.
- Computer Restrictions: graphic calculator TI-83 or TI-83+.
- Activities: the student will practice each outcome via the homework given in the textbook and online.
- Evaluation: the student achievement of each outcome will be assessed via:
- in-class quizzes: taken from the textbook's exercise sets;
- online quizzes: based on the course material, provided by Webwork, http://webwork.marshall.edu/webwork2/F17-Math-231-Saveliev/;
- in-class tests: based on the textbook's exercises;
- projects: written applications of calculus in science and engineering.
- Grade Breakdown:
- participation: $5\%$,
- quizzes: $25\%$,
- project: $20\%$,
- midterm: $20\%$,
- final exam: $30\% $,
i.e., the total score is the following weighted average of the five scores: $$\text{TOTAL }= .05 \times P + .25\times Q + .20\times P + .20\times M + .30\times F.$$
For other details, see Course policy.
Contents
Lectures
They will appear here as the course progresses.
Notes:
- Set 1
- Introduction to calculus of several variables
- Set 2
- Functions in higher dimensions
- Set 3
- Differential calculus of parametric curves
- Set 4
- Functions of several variables
- Set 5
- Integrals of functions of several variables
- Set 6
YouTube channel: Calculus III
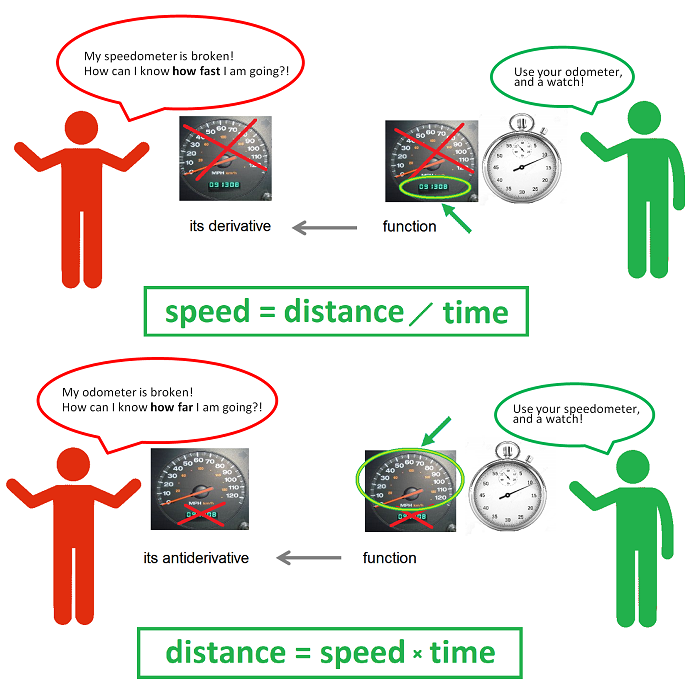
Calculus in one picture...
Projects
The details and the project statements are here: Calculus Illustrated -- Projects.
Instructions:
- A group should contain three or four persons.
- There may be short presentations half-way.
- Your submission should be both on paper and in a digital format such as PDF (it will be linked here).
- It is a good idea to go digital from the beginning; for example, write with Latex or MS Word, draw with MS Paint, analyze data with MS Excel or Google spreadsheets.
- Include: the name, the title, introduction, conclusions, labeled pictures and tables, references, etc.
- The Excel file with the “free fall” equations is here for download, some explanations are here.
- Due date: one week before the last class: Thursday, November 30th
Groups:
- 1. Chloe Marcum, Cristoph Hart, Forest Rowley, and Faith Hensley: (10a) Several buildings with curved walls have been accused of causing sunburns and other damage by focusing the sunlight; is it possible? We chose this project statement because it a good representative of calculus in the real world. It also demonstrates the importance of calculating things correctly, such as measurements, because if not, bad things could happen, in this case - burning. This project can demonstrate topics of Calculus III because it involves a surface and you have to determine the normal vector to the point in which the light hits the surface on the building. Also, the intersection point of all the normal vectors will be the focus of the mirror/window.
- 2. Andrew Meredith, Andrew Short, Emma Lockyer, and Josh Mason: (4a) I would like to use a cannon with a muzzle velocity of 100 feet per second to bombard the inside of a fortification 300 feet away with walls 20 feet high. The project goal is to find the right parameters to get the projectile that travels at 100 feet per second from the cannon to shoot over the wall that is 300 feet away and 20 feet high. To apply calculus three concepts, we intend to include how you could make the projectile land when there is some sort of wind resistance during the path of the projectile flight. How we plan to implement this is making the curve of projectile motion and parameterizing it and including a z-axis as wind can come from not a strictly from North, West, East, or South but could come from in between those directions diagonally or multiple directions making the wind a vector because it has a magnitude. This would make the cannon adjustments not only from a certain degree up and down but also left to right.
- 3. Samuel Wood, Kevin Hoops, Moaz Agha: (7) How fast does the shadow of a falling ball on a sliding ladder move? For our proposal for the project is that we break down each section individually. To begin with, we must determine the position of the ball with respect to time from the acceleration due to gravity. Because of the shadow of the ball is the issue we must find the angle of the sun to the horizontal. Due to the ladder being introduced to the problem we must investigate the forces on the ladder and structure and how it affects the downward acceleration when sliding against a surface. We must investigate how the shadow of an object moving that is also in play with another object moving is affected. Our hypothesis is that the rate of which the shadow moves will slow down as the object moves with the ladder, since both will be in motion. Excel and pictures will be provided to show demonstration along with other sources provided.
- 4. Dan Allen: (11a) Where should I stand in order to be best illuminated by two light bulbs on the ceiling if the amount of light is inversely proportional to the square of the distance? The reason this project is important is because there are many real life applications that this scenario could potentially be describing. The first scenario that comes to my mind is a stage at a theater. On a stage in a theater, lighting is extremely important because theaters are dark and the lighting drastically impacts the appearance of the stage and whoever is present on it, whether that be a speaker, cast for a play, comedian, etc. This is a calculus 3 and not 1 project because this project is 3-dimensional whereas calculus 1 is one-dimensional. Ultimately, with this project, I would like to find out where one should stand in order to be best illuminated by two light bulbs on the ceiling if the amount of light is inversely proportional to the square of the distance.
- 5. Sawyer, Mayson, and Jess: (10c) Is possible that a flying object such as the Stealth bomber can be invisible to the radar? Our group is seeking to design a RADAR array that can detect stealth aircraft utilizing methods such as dot product, vector magnitudes, and the angle between vectors (using cosα[(a-b)/(|a|*|b|)]). The current problem with standard RADAR is the fact that they can be evaded by aircraft like the B-2 stealth bomber due to the angles of reflection when the radio waves bounce off the aircraft. When a standard RADAR is looking for signals, it is operating under the assumption that the aircraft will have a surface that will reflect the radio waves back perfectly into the dish. Because the advantages of aerodynamics outweigh the advantages of stealth, and having both is extremely expensive, when designing aircrafts, they prioritize the designs that favor less air resistance. Since the planes they manufacture favor aerodynamics, that means that most of them have smooth edges and even curves, so when the radio waves hit it, most if not every time, they are reflected back perfectly into the dish, allowing the RADAR to pinpoint the location of the craft. Therefore, the stealth crafts with the unfavorable angles can pass through undetected through the standard RADAR system. Through our design, we seek to be able to pinpoint the location of any aircrafts, stealth or not, based on the calculus 3 concepts we explained before.
- 6. Ethan Frazier, Chris Kirk, Ryan Jarrell: (19) "What does the trajectory of a satellite become when its rocket engine is turned on?"
Description
Tutoring
The tutoring lab is in Smith Hall 625. It will be open Monday through Thursday from 10am to 4pm and 5:00pm to 6:30pm, and on Friday from 10:00am to noon. As usual, we offer free drop-in tutoring for math and statistics classes through Calc 3.
The lab will open on the second week of classes, beginning August 28 and running through the end of the semester. The lab is not open during finals week.
Also, the university tutoring center is in Smith Communications on the second floor.
Exams
- Calculus III -- Fall 2017 -- midterm: Thursday, October 12
- Calculus III -- Fall 2017 -- final: Monday, December 11, 12:45-2:45, same place.
Each old exam below is a small sample of the types of problems that may appear: